人教B版高中数学选修2-3 2.2.3独立重复试验与二项分布教学课件 共16张PPT
文档属性
| 名称 | 人教B版高中数学选修2-3 2.2.3独立重复试验与二项分布教学课件 共16张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-10 08:09:06 | ||
图片预览




文档简介
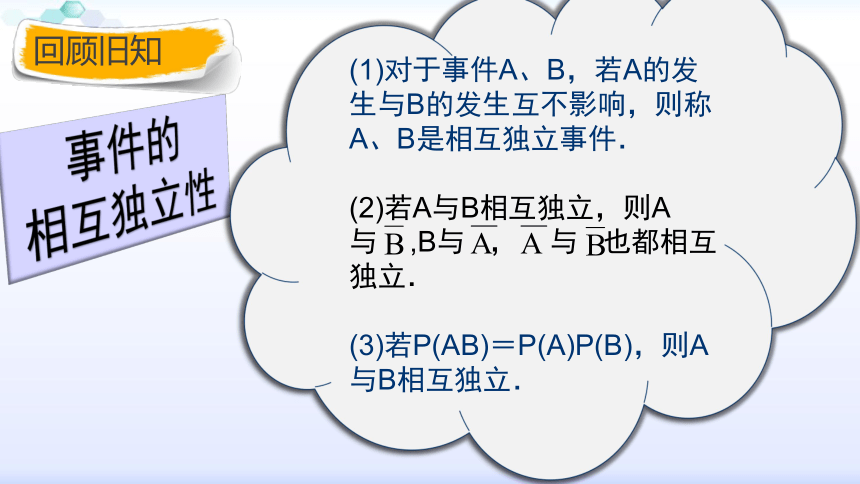
课件16张PPT。欢迎来到我的课堂! 独立重复试验与二项分布事件的
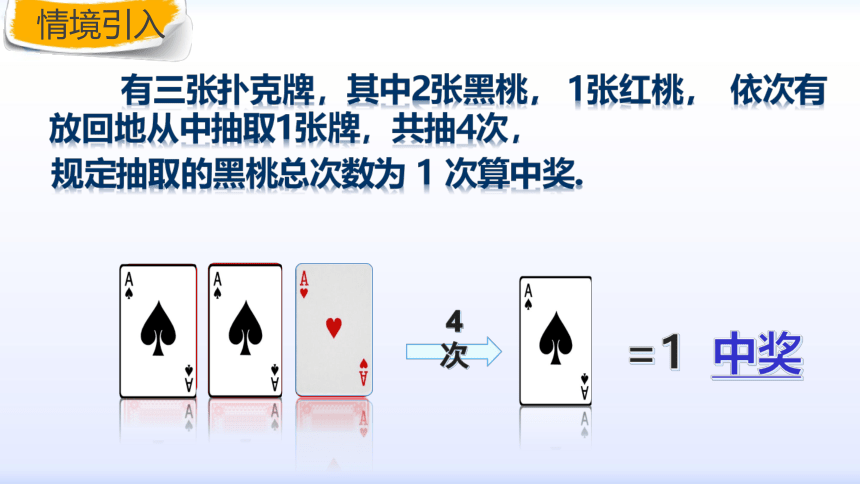
相互独立性有三张扑克牌,其中2张黑桃,1张红桃, 依次有放回地从中抽取1张牌,共抽4次,=1 中奖
规定抽取的黑桃总次数为 1 次算中奖.1. 每次抽取扑克牌的条件是否相同?2. 每次抽取的结果是否受上次影响? n次独立重复试验?你还能想到生活中或者之前的学习中遇到的n次独立重复试验吗?(一)定义?n次独立重复试验(二)概念辨析√××√√ 二项分布 投掷一枚图钉,设针尖向上的概率为p,则针尖向下的概率为1-p.连续掷一枚图钉3次,记出现针尖向上的次数为X,问:
(1)该试验属于独立重复试验吗?
(2)仅出现1次针尖向上的概率是多少?
(3)类似的,连续掷3次图钉,出现k(k=0,1,2,3)次针尖向上的概率是多少? (4)类比当掷n次时,出现k(k=0,1,2,...n)次针尖向上的概率又是多少? 二项分布(一)二项分布的概念此时称随机变量X 服从二项分布,记作X~B(n,p),并称p为成功概率。有三张扑克牌,其中2张黑桃,1张红桃, 依次有放回地从中抽取1张牌,共抽4次,=1 中奖
规定抽取的黑桃总次数为 1 次算中奖.求中奖的概率。(二)概念辨析 例1 某射手每次射击击中目标的概率是0.8,求这名射手在10次射击中,
(1)恰有8次击中目标的概率;
(2)至少有8次击中目标的概率.
(结果保留两个有效数字.)(三)强化提高答案:(1)0.30
(2)0.68课堂小结1.n次独立重复试验2.二项分布 一般地,在相同条件下重复做的n次试验称为n次独立重复试验。 一般地,在n次独立重复实验中,用X表示事件A发生的次数,设每次试验中A发生的概率为p,则1.课后思考题:1.对比二项分布的公式与二项式定理的公式,你能看出它们之间的联系吗?2.二项分布与两点分布有何关系2.作业布置选修2-3 教材58页 练习第 2 题谢谢您的倾听!
相互独立性有三张扑克牌,其中2张黑桃,1张红桃, 依次有放回地从中抽取1张牌,共抽4次,=1 中奖
规定抽取的黑桃总次数为 1 次算中奖.1. 每次抽取扑克牌的条件是否相同?2. 每次抽取的结果是否受上次影响? n次独立重复试验?你还能想到生活中或者之前的学习中遇到的n次独立重复试验吗?(一)定义?n次独立重复试验(二)概念辨析√××√√ 二项分布 投掷一枚图钉,设针尖向上的概率为p,则针尖向下的概率为1-p.连续掷一枚图钉3次,记出现针尖向上的次数为X,问:
(1)该试验属于独立重复试验吗?
(2)仅出现1次针尖向上的概率是多少?
(3)类似的,连续掷3次图钉,出现k(k=0,1,2,3)次针尖向上的概率是多少? (4)类比当掷n次时,出现k(k=0,1,2,...n)次针尖向上的概率又是多少? 二项分布(一)二项分布的概念此时称随机变量X 服从二项分布,记作X~B(n,p),并称p为成功概率。有三张扑克牌,其中2张黑桃,1张红桃, 依次有放回地从中抽取1张牌,共抽4次,=1 中奖
规定抽取的黑桃总次数为 1 次算中奖.求中奖的概率。(二)概念辨析 例1 某射手每次射击击中目标的概率是0.8,求这名射手在10次射击中,
(1)恰有8次击中目标的概率;
(2)至少有8次击中目标的概率.
(结果保留两个有效数字.)(三)强化提高答案:(1)0.30
(2)0.68课堂小结1.n次独立重复试验2.二项分布 一般地,在相同条件下重复做的n次试验称为n次独立重复试验。 一般地,在n次独立重复实验中,用X表示事件A发生的次数,设每次试验中A发生的概率为p,则1.课后思考题:1.对比二项分布的公式与二项式定理的公式,你能看出它们之间的联系吗?2.二项分布与两点分布有何关系2.作业布置选修2-3 教材58页 练习第 2 题谢谢您的倾听!
