人教版高中数学必修三2.2.2用样本的数字特征估计总体的数字特征教学课件 共26张PPT
文档属性
| 名称 | 人教版高中数学必修三2.2.2用样本的数字特征估计总体的数字特征教学课件 共26张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 261.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-10 00:00:00 | ||
图片预览





文档简介
课件26张PPT。12.2.2 用样本的数字特征估计总体的数字特征
众数、中位数、平均数
2. 标准差
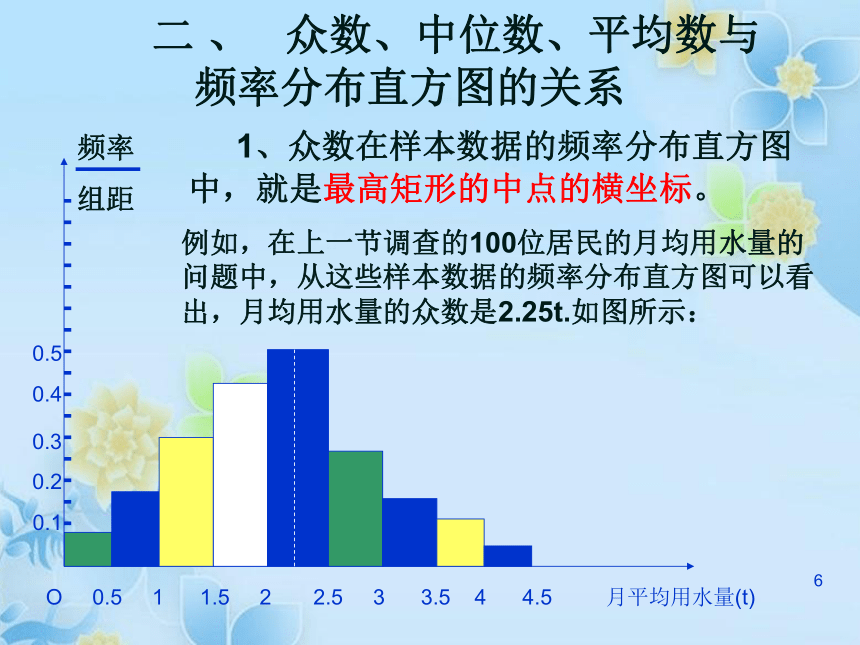
1众数、中位数、平均数1一 众数、中位数、平均数的概念 中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数. 众数:在一组数据中,出现次数最多的数据叫做这组数据的众数. 众数、中位数、平均数都是描述一组数据的集中趋势的特征数,只是描述的角度不同,其中以平均数的应用最为广泛.1 练习: 在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示: 分别求这些运动员成绩的众数,中位数与平均数 解:在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75.
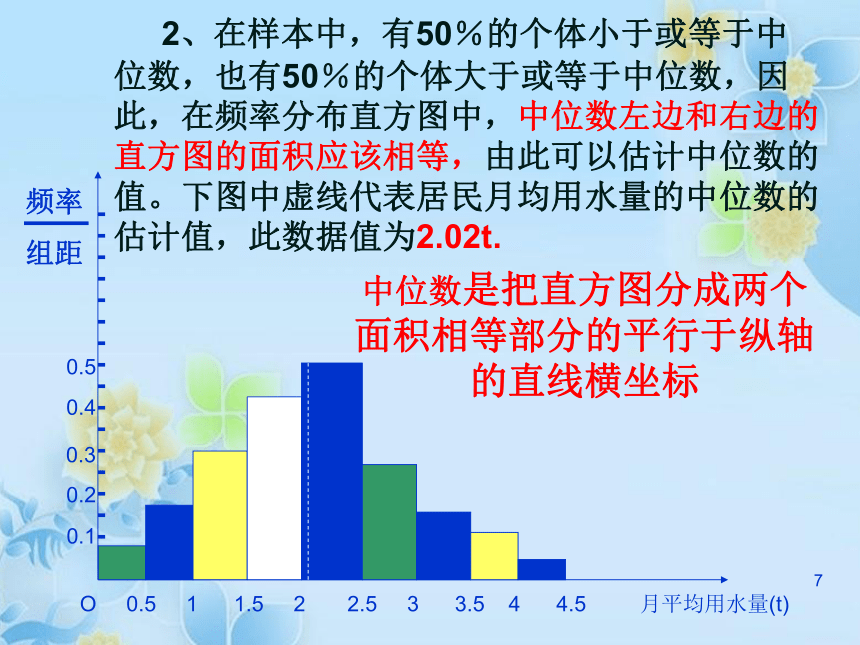
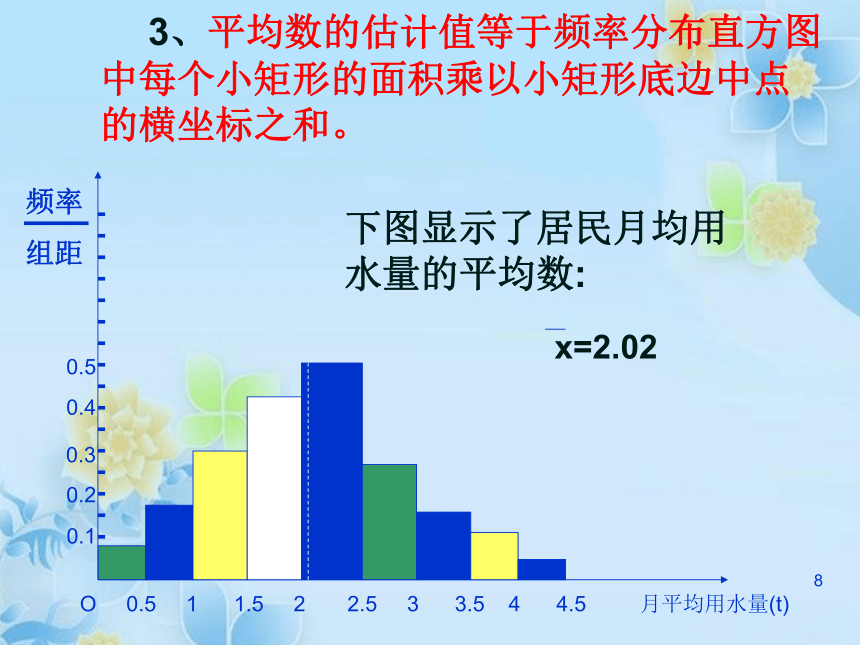
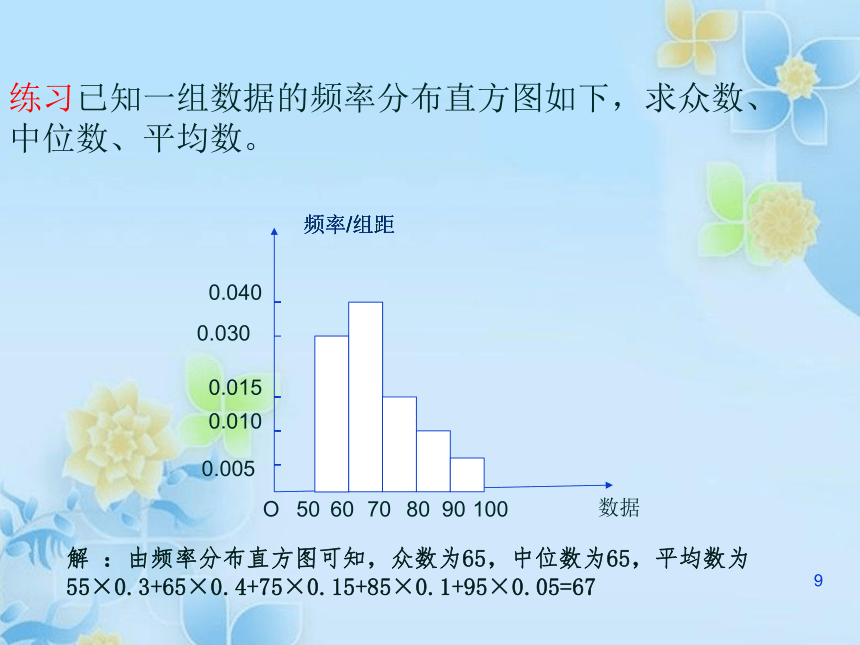
上面表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,即这组数据的中位数是1.70;1 这组数据的平均数是答:17名运动员成绩的众数、中位数、平均数依次是1.75(米)、1.70(米)、1.69(米). 1例如,在上一节调查的100位居民的月均用水量的问题中,从这些样本数据的频率分布直方图可以看出,月均用水量的众数是2.25t.如图所示: 二 、 众数、中位数、平均数与频率分布直方图的关系 1、众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。1 2、在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值。下图中虚线代表居民月均用水量的中位数的估计值,此数据值为2.02t. 中位数是把直方图分成两个面积相等部分的平行于纵轴的直线横坐标1 3、平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。下图显示了居民月均用水量的平均数:1练习已知一组数据的频率分布直方图如下,求众数、中位数、平均数。
900.030频率/组距频率/组距频率/组距解 :由频率分布直方图可知,众数为65,中位数为65,平均数为
55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=671三 三种数字特征的优缺点 1、众数体现了样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征.如上例中众数是2.25t,它告诉我们,月均用水量为2.25t的居民数比月均用水量为其它数值的居民数多,但它并没有告诉我们多多少.1 2、中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点。如上例中假设有某一用户月均用水量为10t,那么它所占频率为0.01,几乎不影响中位数,但显然这一极端值是不能忽视的。1 3、由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具有的性质。也正因如此 ,与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。 1标准差 1.如何根据样本频率分布直方图,分别估
计总体的众数、中位数和平均数? (1)众数:最高矩形下端中点的横坐标。 (2)中位数:直方图面积平分线与横轴交点
的横坐标。 (3)平均数:每个小矩形的面积与小矩形底
边中点的横坐标的乘积之和。知识回顾1 如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:甲:7 8 7 9 5 4 9 10 7 4乙:9 5 7 8 7 6 8 6 7 7如果你是教练,你应当如何对这次射击作出评价?如果看两人本次射击的平均成绩,由于 两人射击 的平均成绩是一样的.那么两个人的水平就没有什么差异吗?
1(甲)45678910环数频率0.10.20.3频率(乙) 直观上看,还是有差异的.如:甲成绩比较分散,乙成绩相对集中(如上图所示).
因此,我们还需要从另外的角度来考察这两组数据.例如:在作统计图表时提到过的极差.
甲的环数极差=10-4=6 乙的环数极差=9-5=4.
但是极差对极端值非常敏感1 由于上式含有绝对值,运算不太方便,因此,通常改用如下公式来计算标准差.一个样本中的个体与平均数之间的距离关系可用下图表示:考虑一个容量为2的样本:1 考察样本数据的分散程度,最常用的统计量是标准差显然,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.用计算器可算出甲,乙两人的的成绩的标准差上面两组数据的离散程度与标准差之间的关系可用图直观地表示出来.1例题1:画出下列四组样本数据的条形图,说明它们的异同点.解:四组样本数据的条形图是:1频率31245678o0.10.20.30.40.50.60.70.80.91.0S=1.49(3)(4)四组数据的平均数都是5.0,标准差分别是0.00,0.82,1.49,2.83.
虽然它们有相同的平均数,但是它们有不同的标准差,说明数据的分散程度是不一样的.1例2 甲乙两人同时生产内径为25.40mm的一种零件.为了对两人的生产质量进行评比,从他们生产的零件中各抽出20件,量得其内径尺寸如下(单位:mm)甲 25.46, 25.32, 25.45, 25.39, 25.36
25.34, 25.42, 25.45, 25.38, 25.42
25.39, 25.43, 25.39, 25.40, 25.44
25.40, 25.42, 25.35, 25.41, 25.39乙 25.40, 25.43, 25.44, 25.48, 25.48
25.47, 25.49, 25.49, 25.36, 25.34
25.33, 25.43, 25.43, 25.32, 25.47
25.31, 25.32, 25.32, 25.32, 25.48 从生产的零件内径的尺寸看,谁生产的质量较高?1解:用计算器计算可得:1所以12.一组数据中的每一个数据都减去80,得一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是__________
81.24.41.某中学人数相等的甲、乙两班学生参加同一次数学测试,两班平均分和方差分别为 甲 =82分,乙 =82分, 甲=245, 乙 =190,那么成绩较为整齐的是( )
A.甲班 B.乙班 C.两班一样齐 D.无法确定B练习13.甲、乙、丙、丁四名射击手在选拔赛中的平均环数 及其标准差s如下图所示,则选送决赛的最佳人选应是_______乙1小结:1 . 众数、中位数、平均数的概念
2. 众数、中位数、平均数与频率分布直方图的关系
3. 三种数字特征的优缺点
4. 什么是标准差?
5. 如何利用标准差刻画数据的离散程度?
2. 标准差
1众数、中位数、平均数1一 众数、中位数、平均数的概念 中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数. 众数:在一组数据中,出现次数最多的数据叫做这组数据的众数. 众数、中位数、平均数都是描述一组数据的集中趋势的特征数,只是描述的角度不同,其中以平均数的应用最为广泛.1 练习: 在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示: 分别求这些运动员成绩的众数,中位数与平均数 解:在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75.
上面表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,即这组数据的中位数是1.70;1 这组数据的平均数是答:17名运动员成绩的众数、中位数、平均数依次是1.75(米)、1.70(米)、1.69(米). 1例如,在上一节调查的100位居民的月均用水量的问题中,从这些样本数据的频率分布直方图可以看出,月均用水量的众数是2.25t.如图所示: 二 、 众数、中位数、平均数与频率分布直方图的关系 1、众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。1 2、在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值。下图中虚线代表居民月均用水量的中位数的估计值,此数据值为2.02t. 中位数是把直方图分成两个面积相等部分的平行于纵轴的直线横坐标1 3、平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。下图显示了居民月均用水量的平均数:1练习已知一组数据的频率分布直方图如下,求众数、中位数、平均数。
900.030频率/组距频率/组距频率/组距解 :由频率分布直方图可知,众数为65,中位数为65,平均数为
55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=671三 三种数字特征的优缺点 1、众数体现了样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征.如上例中众数是2.25t,它告诉我们,月均用水量为2.25t的居民数比月均用水量为其它数值的居民数多,但它并没有告诉我们多多少.1 2、中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点。如上例中假设有某一用户月均用水量为10t,那么它所占频率为0.01,几乎不影响中位数,但显然这一极端值是不能忽视的。1 3、由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具有的性质。也正因如此 ,与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。 1标准差 1.如何根据样本频率分布直方图,分别估
计总体的众数、中位数和平均数? (1)众数:最高矩形下端中点的横坐标。 (2)中位数:直方图面积平分线与横轴交点
的横坐标。 (3)平均数:每个小矩形的面积与小矩形底
边中点的横坐标的乘积之和。知识回顾1 如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:甲:7 8 7 9 5 4 9 10 7 4乙:9 5 7 8 7 6 8 6 7 7如果你是教练,你应当如何对这次射击作出评价?如果看两人本次射击的平均成绩,由于 两人射击 的平均成绩是一样的.那么两个人的水平就没有什么差异吗?
1(甲)45678910环数频率0.10.20.3频率(乙) 直观上看,还是有差异的.如:甲成绩比较分散,乙成绩相对集中(如上图所示).
因此,我们还需要从另外的角度来考察这两组数据.例如:在作统计图表时提到过的极差.
甲的环数极差=10-4=6 乙的环数极差=9-5=4.
但是极差对极端值非常敏感1 由于上式含有绝对值,运算不太方便,因此,通常改用如下公式来计算标准差.一个样本中的个体与平均数之间的距离关系可用下图表示:考虑一个容量为2的样本:1 考察样本数据的分散程度,最常用的统计量是标准差显然,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.用计算器可算出甲,乙两人的的成绩的标准差上面两组数据的离散程度与标准差之间的关系可用图直观地表示出来.1例题1:画出下列四组样本数据的条形图,说明它们的异同点.解:四组样本数据的条形图是:1频率31245678o0.10.20.30.40.50.60.70.80.91.0S=1.49(3)(4)四组数据的平均数都是5.0,标准差分别是0.00,0.82,1.49,2.83.
虽然它们有相同的平均数,但是它们有不同的标准差,说明数据的分散程度是不一样的.1例2 甲乙两人同时生产内径为25.40mm的一种零件.为了对两人的生产质量进行评比,从他们生产的零件中各抽出20件,量得其内径尺寸如下(单位:mm)甲 25.46, 25.32, 25.45, 25.39, 25.36
25.34, 25.42, 25.45, 25.38, 25.42
25.39, 25.43, 25.39, 25.40, 25.44
25.40, 25.42, 25.35, 25.41, 25.39乙 25.40, 25.43, 25.44, 25.48, 25.48
25.47, 25.49, 25.49, 25.36, 25.34
25.33, 25.43, 25.43, 25.32, 25.47
25.31, 25.32, 25.32, 25.32, 25.48 从生产的零件内径的尺寸看,谁生产的质量较高?1解:用计算器计算可得:1所以12.一组数据中的每一个数据都减去80,得一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是__________
81.24.41.某中学人数相等的甲、乙两班学生参加同一次数学测试,两班平均分和方差分别为 甲 =82分,乙 =82分, 甲=245, 乙 =190,那么成绩较为整齐的是( )
A.甲班 B.乙班 C.两班一样齐 D.无法确定B练习13.甲、乙、丙、丁四名射击手在选拔赛中的平均环数 及其标准差s如下图所示,则选送决赛的最佳人选应是_______乙1小结:1 . 众数、中位数、平均数的概念
2. 众数、中位数、平均数与频率分布直方图的关系
3. 三种数字特征的优缺点
4. 什么是标准差?
5. 如何利用标准差刻画数据的离散程度?
