3.1.1 两角差的余弦公式课件34张PPT
文档属性
| 名称 | 3.1.1 两角差的余弦公式课件34张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-10 00:00:00 | ||
图片预览









文档简介
课件34张PPT。第三章 三角恒等变换
3.1 两角和与差的正弦、余弦和正切公式
3.1.1 两角差的余弦公式 某城市的电视发射塔建在市郊的一座小山上.如图所示, 在地平面上有一点A,测得A,C两点间距离约为60米,从A观测电视发射塔的视角(∠CAD)约为45°, ∠CAB=15°.求这座电视发射塔的高度.BDAC6045°15°对于30°,45°,60°等特殊角的三角函数值可以直接写出,利用诱导公式还可进一步求出150°,210°,315°等角的三角函数值.我们希望再引进一些公式,能够求更多的非特殊角的三角函数值,同时也为三角恒等变换提供理论依据.1.会用向量的数量积推导出两角差的余弦公式.(难点)
2.掌握两角差的余弦公式和两角余弦的差,并能正确的运用公式进行简单三角函数式的化简、求值.(重点)
3.掌握“变角”和“拆角”的方法.(重点、难点)微课1 两角差的余弦公式的推导若 为两个任意角, 则
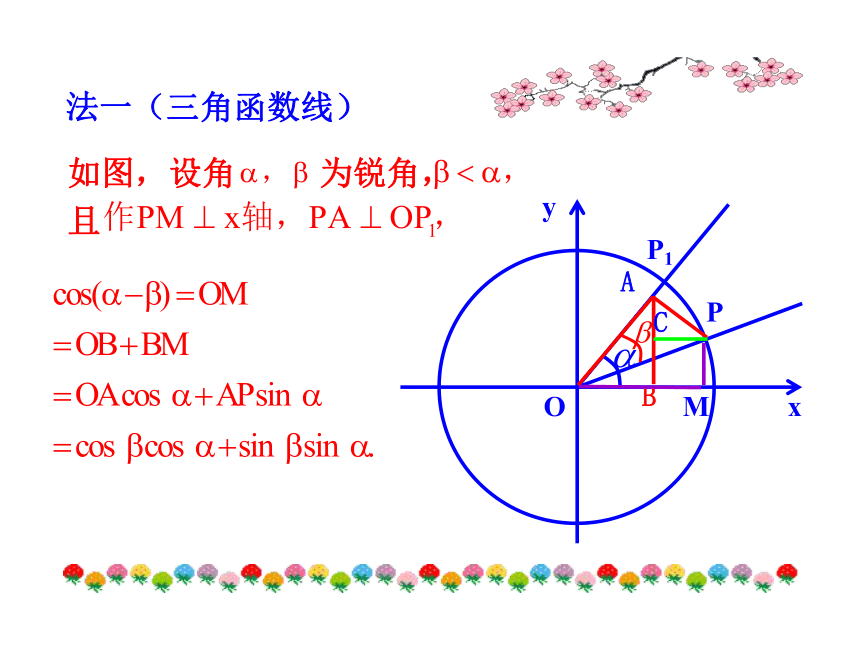
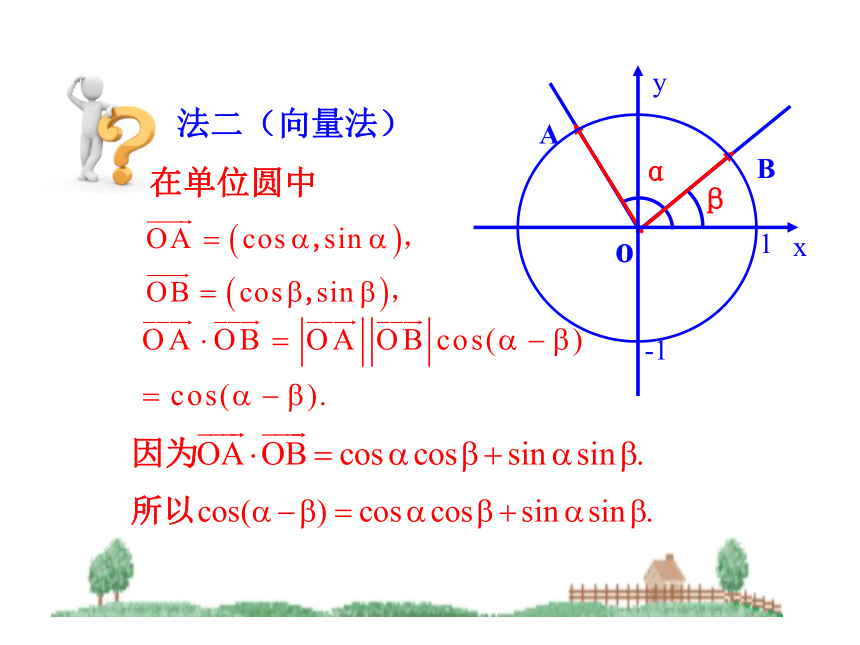
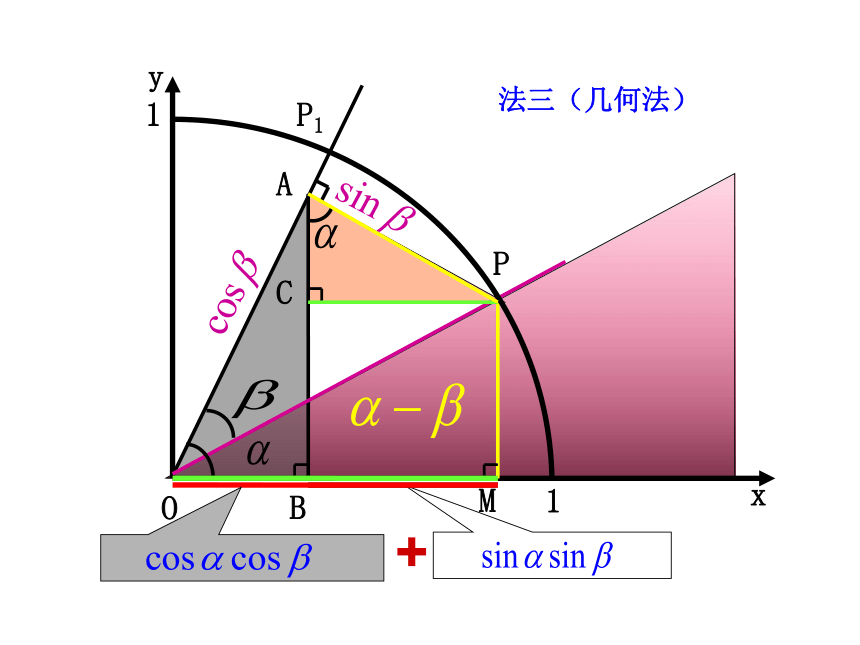
成立吗?提示:要获得 的表达式需要哪些已学过的知识?提示:PP1Oxy法一(三角函数线)在单位圆中法二(向量法)xyPP1MBOAC+11法三(几何法)差角的余弦公式一句话要诀:“余余正正符号反”B【即时练习】微课2 两角差的余弦公式的应用完成本题后,你会求 的值吗?把非特殊角变为
特殊角,把未知角变为已知角.C【变式练习】利用同角的三角函数关系式求值时,要注意角的范围.先求两角的正、余弦值,再代入差角的余弦公式求值.【方法规律】【变式练习】【解题关键】【解析】 利用差角公式求值时,常常进行角的拆分与组合.即公式的变形应用.【变式练习】【互动探究】AC【解析】【解析】【解析】1.两角差的余弦公式:2.已知一个角的正弦(或余弦)值,求该角的余弦(或正弦)值时, 要注意该角所在的象限,从而确定该角的三角函数值符号.3.在差角的余弦公式中, 既可以是单角,也可以是复角,运用时要注意角的变换,
如 , 等.
同时,公式的应用具有灵活性,解题时要注意正向、逆向和变式形式的选择.长期的心灰意懒以及烦恼足以致人于贫病枯萎.
——布朗
3.1 两角和与差的正弦、余弦和正切公式
3.1.1 两角差的余弦公式 某城市的电视发射塔建在市郊的一座小山上.如图所示, 在地平面上有一点A,测得A,C两点间距离约为60米,从A观测电视发射塔的视角(∠CAD)约为45°, ∠CAB=15°.求这座电视发射塔的高度.BDAC6045°15°对于30°,45°,60°等特殊角的三角函数值可以直接写出,利用诱导公式还可进一步求出150°,210°,315°等角的三角函数值.我们希望再引进一些公式,能够求更多的非特殊角的三角函数值,同时也为三角恒等变换提供理论依据.1.会用向量的数量积推导出两角差的余弦公式.(难点)
2.掌握两角差的余弦公式和两角余弦的差,并能正确的运用公式进行简单三角函数式的化简、求值.(重点)
3.掌握“变角”和“拆角”的方法.(重点、难点)微课1 两角差的余弦公式的推导若 为两个任意角, 则
成立吗?提示:要获得 的表达式需要哪些已学过的知识?提示:PP1Oxy法一(三角函数线)在单位圆中法二(向量法)xyPP1MBOAC+11法三(几何法)差角的余弦公式一句话要诀:“余余正正符号反”B【即时练习】微课2 两角差的余弦公式的应用完成本题后,你会求 的值吗?把非特殊角变为
特殊角,把未知角变为已知角.C【变式练习】利用同角的三角函数关系式求值时,要注意角的范围.先求两角的正、余弦值,再代入差角的余弦公式求值.【方法规律】【变式练习】【解题关键】【解析】 利用差角公式求值时,常常进行角的拆分与组合.即公式的变形应用.【变式练习】【互动探究】AC【解析】【解析】【解析】1.两角差的余弦公式:2.已知一个角的正弦(或余弦)值,求该角的余弦(或正弦)值时, 要注意该角所在的象限,从而确定该角的三角函数值符号.3.在差角的余弦公式中, 既可以是单角,也可以是复角,运用时要注意角的变换,
如 , 等.
同时,公式的应用具有灵活性,解题时要注意正向、逆向和变式形式的选择.长期的心灰意懒以及烦恼足以致人于贫病枯萎.
——布朗
