人教版八年级下册课件 18.2.3-正方形 (共27张PPT)
文档属性
| 名称 | 人教版八年级下册课件 18.2.3-正方形 (共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-10 17:22:37 | ||
图片预览



文档简介
18.2.3 正方形 (1)
----正方形的性质
学习目标
1.理解正方形与平行四边形、矩形、菱形概
念之间的联系和区别;
2.能用正方形的定义、性质进行推理与计算.
学习重点
正方形与平行四边形、矩形、菱形的联系.
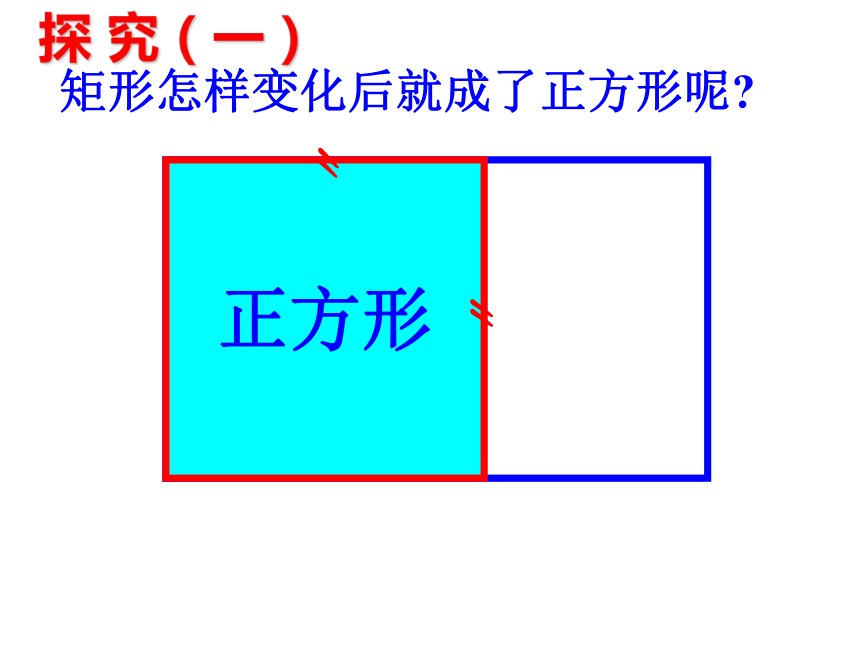
矩 形
正方形
〃
〃
矩形怎样变化后就成了正方形呢?
探 究(一)
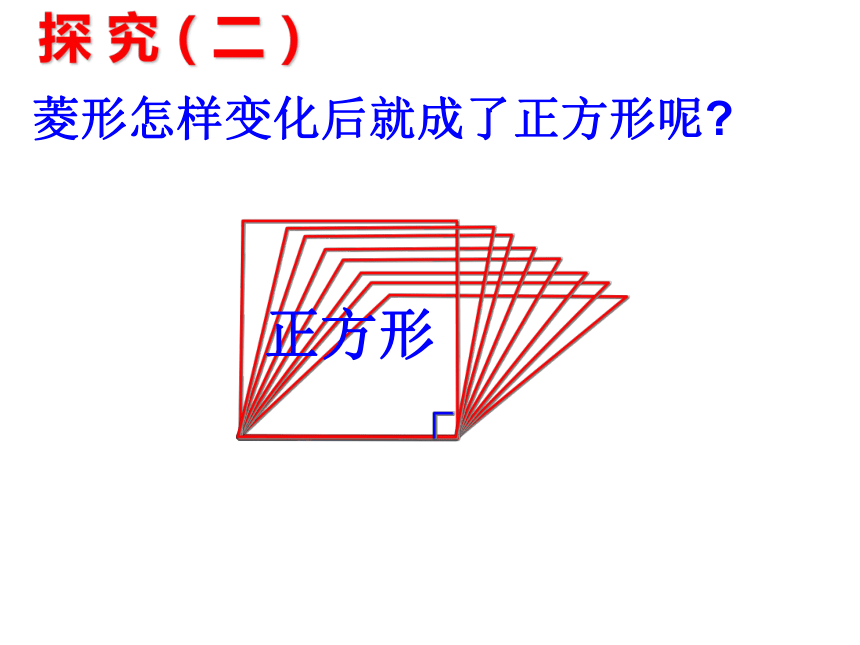
探 究(二)
菱形怎样变化后就成了正方形呢?
正方形
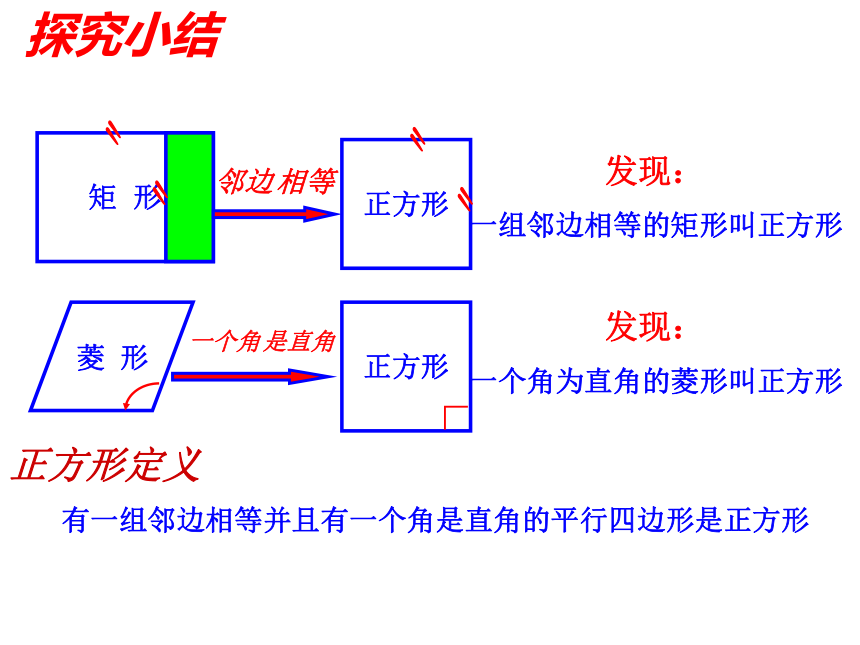
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形叫正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形叫正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
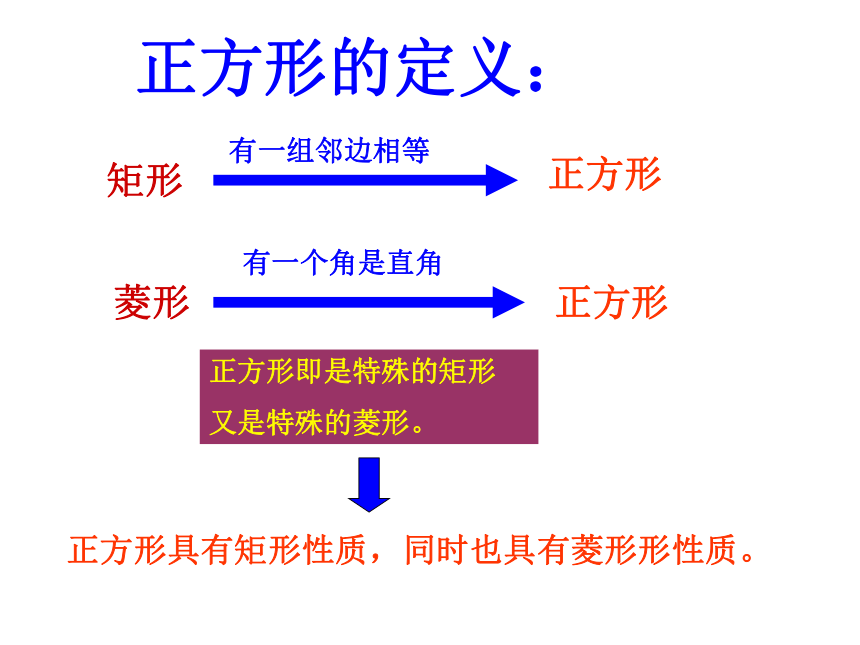
正方形的定义:
正方形即是特殊的矩形
又是特殊的菱形。
正方形具有矩形性质,同时也具有菱形形性质。
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
正方形的性质=
正方形是轴对称图形,它的对称轴是什么?
快速抢答
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
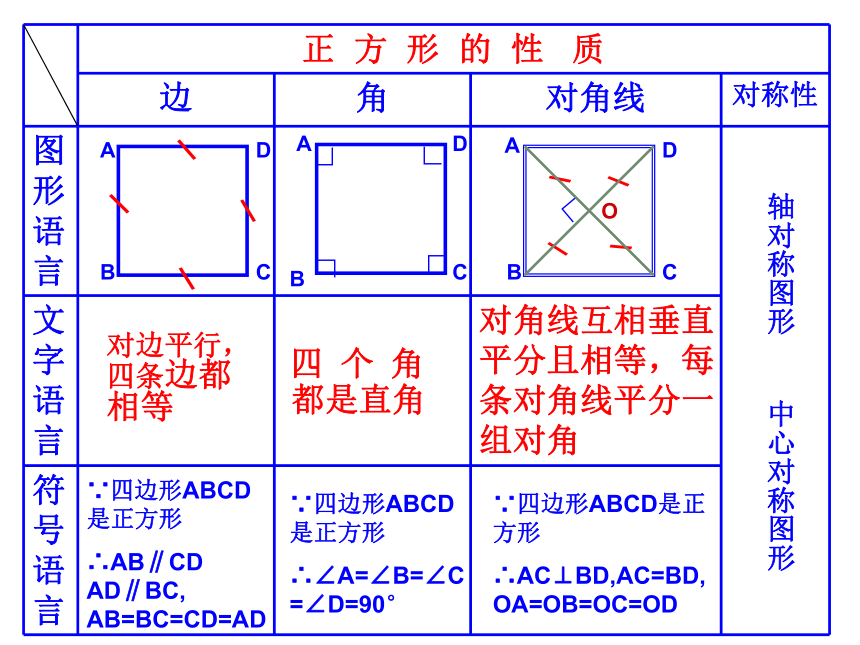
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD 是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
正 方 形 的 性 质
边 角 对角线 对称性
图形语言
文字语言
符号语言
正方形、矩形、菱形以及平行四边形四者之间的关系:
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
四边形
平行四边形
矩形
菱形
正方形
平行四边形
矩形
四边形
菱形
正
方
形
平行四边形、矩形、菱形、正方形之间关系
例1:求证: 正方形的两条对角线把这个正方形分成四个
全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角
线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO
是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形:
△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
1.(1)把一张长方形纸片按如图方式折一下,就可以裁
出正方形纸片.为什么?
(2)如何从一块长方形木板中裁出一块最大的正方形木
板呢?
解:由已知,对折后可得:所得的四边形有三个
直角,且一组邻边相等,所以可以裁出正方
形纸片。
解:在长方形最长的两边,截取长度等于“长方形的短边的长度”,
这样就可以截出面积最大的正方形
课堂练习
( P59页 )
2.如图,ABCD是一块正方形场地.小华和小芳在
AB边上取定了一点E,测量知,EC= 30m,
EB=10m.这块场地的面积和对角线分别是多少?
解:根据勾股定理:
BC2= EC2- EB2 = 302 – 102 = 800
∴BC=
∴这块场地的面积=
= 800
对角线AC =
= 40
30
10
例2:已知正方形ABCD
(1)若一条对角线BD长为2cm,求这个正方形的
周长、面积。
2
(2)若E为对角线上一点,连接EA、EC。
EA = EC吗?说说你的理由。
E
例2:已知正方形ABCD
1
2
?
?
(3)若BA=BE,求∠ AED的大小。
E
例2:已知正方形ABCD
45°
67.5°
67.5°
112.5°
例3:已知正方形ABCD, M是AD上的点, ME⊥ BD,
MF⊥ AC,垂足分别为E、F
(1) 若对角线AC=12cm,
求ME+MF的长。
A
B
C
D
O
M
F
E
(2)若M是AD上的一个动
点,ME+MF的长度是
否发生改变?
ME + MF = 6cm
例4:已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接DE,连接BG并延长交DE于F.
(1)求证:△BCG≌△DCE;
1
2
例4:已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接DE,连接BG并延长交DE于F.
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断
四边形BGDE′是什么特殊四边形?并说明理由.
例5:在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜
想AB、AC、BE之间的关系,并证明你的猜想.
A
D
C
B
E
F
AB + BE = AC
截短法
1
2
例5:在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜
想AB、AC、BE之间的关系,并证明你的猜想.
A
D
C
B
E
F
AB + BE = AC
截短法
1
2
例5:在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜
想AB、AC、BE之间的关系,并证明你的猜想.
A
D
C
B
E
G
AB + BE = AC
补长法
1
2
例5:在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜
想AB、AC、BE之间的关系,并证明你的猜想.
A
D
C
B
E
G
AB + BE = AC
补长法
1
2
3
4
5
边
对角线
角
正方形对边平行 四边相等
正方形的四个角都是直角
正方形的对角线相等,互相垂直平分,每条对角线平分一组对角。
正方形是中心对称图形,它也是轴对称图形
正方形是一个完美的图形
作业
课本P62页第 15 题
练习册 P 28-30 页
课本P68页第 8 题
----正方形的性质
学习目标
1.理解正方形与平行四边形、矩形、菱形概
念之间的联系和区别;
2.能用正方形的定义、性质进行推理与计算.
学习重点
正方形与平行四边形、矩形、菱形的联系.
矩 形
正方形
〃
〃
矩形怎样变化后就成了正方形呢?
探 究(一)
探 究(二)
菱形怎样变化后就成了正方形呢?
正方形
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形叫正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形叫正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
正方形的定义:
正方形即是特殊的矩形
又是特殊的菱形。
正方形具有矩形性质,同时也具有菱形形性质。
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
正方形的性质=
正方形是轴对称图形,它的对称轴是什么?
快速抢答
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD 是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
正 方 形 的 性 质
边 角 对角线 对称性
图形语言
文字语言
符号语言
正方形、矩形、菱形以及平行四边形四者之间的关系:
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
四边形
平行四边形
矩形
菱形
正方形
平行四边形
矩形
四边形
菱形
正
方
形
平行四边形、矩形、菱形、正方形之间关系
例1:求证: 正方形的两条对角线把这个正方形分成四个
全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角
线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO
是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形:
△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
1.(1)把一张长方形纸片按如图方式折一下,就可以裁
出正方形纸片.为什么?
(2)如何从一块长方形木板中裁出一块最大的正方形木
板呢?
解:由已知,对折后可得:所得的四边形有三个
直角,且一组邻边相等,所以可以裁出正方
形纸片。
解:在长方形最长的两边,截取长度等于“长方形的短边的长度”,
这样就可以截出面积最大的正方形
课堂练习
( P59页 )
2.如图,ABCD是一块正方形场地.小华和小芳在
AB边上取定了一点E,测量知,EC= 30m,
EB=10m.这块场地的面积和对角线分别是多少?
解:根据勾股定理:
BC2= EC2- EB2 = 302 – 102 = 800
∴BC=
∴这块场地的面积=
= 800
对角线AC =
= 40
30
10
例2:已知正方形ABCD
(1)若一条对角线BD长为2cm,求这个正方形的
周长、面积。
2
(2)若E为对角线上一点,连接EA、EC。
EA = EC吗?说说你的理由。
E
例2:已知正方形ABCD
1
2
?
?
(3)若BA=BE,求∠ AED的大小。
E
例2:已知正方形ABCD
45°
67.5°
67.5°
112.5°
例3:已知正方形ABCD, M是AD上的点, ME⊥ BD,
MF⊥ AC,垂足分别为E、F
(1) 若对角线AC=12cm,
求ME+MF的长。
A
B
C
D
O
M
F
E
(2)若M是AD上的一个动
点,ME+MF的长度是
否发生改变?
ME + MF = 6cm
例4:已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接DE,连接BG并延长交DE于F.
(1)求证:△BCG≌△DCE;
1
2
例4:已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接DE,连接BG并延长交DE于F.
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断
四边形BGDE′是什么特殊四边形?并说明理由.
例5:在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜
想AB、AC、BE之间的关系,并证明你的猜想.
A
D
C
B
E
F
AB + BE = AC
截短法
1
2
例5:在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜
想AB、AC、BE之间的关系,并证明你的猜想.
A
D
C
B
E
F
AB + BE = AC
截短法
1
2
例5:在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜
想AB、AC、BE之间的关系,并证明你的猜想.
A
D
C
B
E
G
AB + BE = AC
补长法
1
2
例5:在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜
想AB、AC、BE之间的关系,并证明你的猜想.
A
D
C
B
E
G
AB + BE = AC
补长法
1
2
3
4
5
边
对角线
角
正方形对边平行 四边相等
正方形的四个角都是直角
正方形的对角线相等,互相垂直平分,每条对角线平分一组对角。
正方形是中心对称图形,它也是轴对称图形
正方形是一个完美的图形
作业
课本P62页第 15 题
练习册 P 28-30 页
课本P68页第 8 题
