人教A版高中数学必修二课件:4.2.2圆与圆的位置关系 共29张PPT
文档属性
| 名称 | 人教A版高中数学必修二课件:4.2.2圆与圆的位置关系 共29张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 424.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-11 18:06:08 | ||
图片预览








文档简介
课件29张PPT。圆与圆的位置关系问题求解1.研究两圆的位置关系可以有两种方法:
数学思想方法:数形结合 等价转化 一、复习回顾2.两圆位置关系与公切线条数:
3.两圆公共弦的直线方程与弦长:
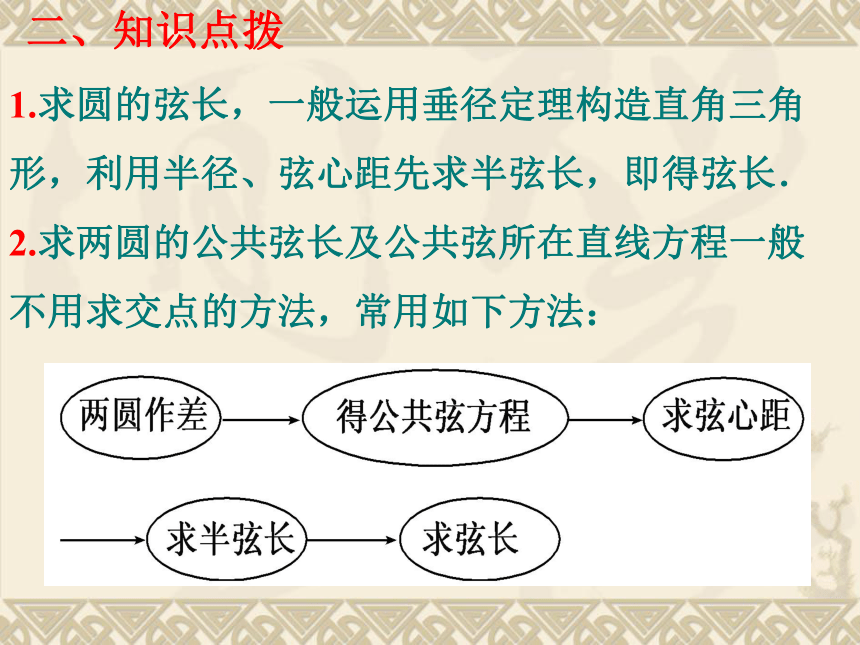
1.求圆的弦长,一般运用垂径定理构造直角三角形,利用半径、弦心距先求半弦长,即得弦长.
2.求两圆的公共弦长及公共弦所在直线方程一般不用求交点的方法,常用如下方法:二、知识点拨 (1)当两圆相交时,此直线为公共弦所在直线;
(2)当两圆相切时,此直线为两圆的公切线;
(3)当两圆相离时,此直线为与两圆连心线垂直的直线.
(4)当两圆为等圆时,此直线为两圆的对称轴.3.常见的圆系方程:
设两相交圆
C1:x2+y2+D1x+E1y+F1=0,
C2:x2+y2+D2x+E2y+F2=0,则:
x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0
(1)λ≠-1时,表示过两相交圆交点的圆(不包括C2);
(2)当λ=-1时,(D1-D2)x+(E1-E2)y+F1-F2=0
表示两圆的公共弦所在的直线方程.
m(x2+y2+D1x+E1y+F1)+n(x2+y2+D2x+E2y+F2)=0 (3)过两圆交点的圆系方程为:
(4)方程
x2+y2+Dx+Ey+F+λ(Ax+By+C)=0,
表示过圆x2+y2+Dx+Ey+F=0与直线
Ax+By+C=0交点的圆(λ为参数).
1.已知两圆x2+y2-2x+10y-24=0和
x2+y2+2x+2y-8=0.
(1)求公共弦所在的直线方程;
(2)求公共弦的长度.
1.两圆的公共弦问题二、基础练习2.解:2.两圆的切线问题例1.已知两圆C1∶x2+y2-2x+10y-24=0和 C2∶x2+y2+2x+2y-8=0 求:
(1)过两圆的交点的直线方程.
(2)圆心在直线 l:x+y=0上,且过两圆的
交点的圆的方程.三、例题解析3.圆系方程问题问题4.两圆相切有关的问题【练习3】求半径为 ,且与圆
切于原点的圆的方程。xyOCBA1.点M在圆心为C1的圆x2+y2+6x-2y+1=0上,点N在圆心为C2的圆x2+y2+2x+4y+1=0上,求 |MN| 的最大值.四、巩固提升3. 求过直线l:2x+y+4=0与圆C:x2+y2+2x-4y+1=0的交点且分别满足下列条件的圆的方程.
(1)过原点;
(2)有最小面积. 4. 已知两圆C1:x2+y2-2x+10y-24=0,
C2:x2+y2+2x+2y-8=0.
(1)求两圆公共弦的方程及其长度;
(2)求以两圆公共弦为直径的圆的方程.
【思路点拨】 (1)先求出公共弦所在直线的方程,再利用半径、弦心距、半弦长构成的直角三角形求解;(2)求出圆心、半径,也可用经过两圆交点的圆系方程求解.x2+y2-4x-2y-1=05.已知一个圆的圆心为M(2,1),且与圆C:x2+y2-3x=0相交于A、B两点,若圆心M到直线AB的距离为 ,求圆M的方程. 1. 在圆(x+1)2+(y+2)2=8上到直线x+y+1=0的距离为 的点有_____个.
2. 在(x+1)2+(y-1)2=r2的圆上是否存在四个点到直线AB:3x-4y-3=0的距离等于1.3r>3五、课后训练4.求经过点M(3,-1) ,且与圆
切于点N(1,2)的圆的方程。yOCMNGxD5.设定点M(-3,4),动点N在圆x2+y2=4上运动,以OM、ON为两边作平行四边形MONP,求点P的轨迹.
数学思想方法:数形结合 等价转化 一、复习回顾2.两圆位置关系与公切线条数:
3.两圆公共弦的直线方程与弦长:
1.求圆的弦长,一般运用垂径定理构造直角三角形,利用半径、弦心距先求半弦长,即得弦长.
2.求两圆的公共弦长及公共弦所在直线方程一般不用求交点的方法,常用如下方法:二、知识点拨 (1)当两圆相交时,此直线为公共弦所在直线;
(2)当两圆相切时,此直线为两圆的公切线;
(3)当两圆相离时,此直线为与两圆连心线垂直的直线.
(4)当两圆为等圆时,此直线为两圆的对称轴.3.常见的圆系方程:
设两相交圆
C1:x2+y2+D1x+E1y+F1=0,
C2:x2+y2+D2x+E2y+F2=0,则:
x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0
(1)λ≠-1时,表示过两相交圆交点的圆(不包括C2);
(2)当λ=-1时,(D1-D2)x+(E1-E2)y+F1-F2=0
表示两圆的公共弦所在的直线方程.
m(x2+y2+D1x+E1y+F1)+n(x2+y2+D2x+E2y+F2)=0 (3)过两圆交点的圆系方程为:
(4)方程
x2+y2+Dx+Ey+F+λ(Ax+By+C)=0,
表示过圆x2+y2+Dx+Ey+F=0与直线
Ax+By+C=0交点的圆(λ为参数).
1.已知两圆x2+y2-2x+10y-24=0和
x2+y2+2x+2y-8=0.
(1)求公共弦所在的直线方程;
(2)求公共弦的长度.
1.两圆的公共弦问题二、基础练习2.解:2.两圆的切线问题例1.已知两圆C1∶x2+y2-2x+10y-24=0和 C2∶x2+y2+2x+2y-8=0 求:
(1)过两圆的交点的直线方程.
(2)圆心在直线 l:x+y=0上,且过两圆的
交点的圆的方程.三、例题解析3.圆系方程问题问题4.两圆相切有关的问题【练习3】求半径为 ,且与圆
切于原点的圆的方程。xyOCBA1.点M在圆心为C1的圆x2+y2+6x-2y+1=0上,点N在圆心为C2的圆x2+y2+2x+4y+1=0上,求 |MN| 的最大值.四、巩固提升3. 求过直线l:2x+y+4=0与圆C:x2+y2+2x-4y+1=0的交点且分别满足下列条件的圆的方程.
(1)过原点;
(2)有最小面积. 4. 已知两圆C1:x2+y2-2x+10y-24=0,
C2:x2+y2+2x+2y-8=0.
(1)求两圆公共弦的方程及其长度;
(2)求以两圆公共弦为直径的圆的方程.
【思路点拨】 (1)先求出公共弦所在直线的方程,再利用半径、弦心距、半弦长构成的直角三角形求解;(2)求出圆心、半径,也可用经过两圆交点的圆系方程求解.x2+y2-4x-2y-1=05.已知一个圆的圆心为M(2,1),且与圆C:x2+y2-3x=0相交于A、B两点,若圆心M到直线AB的距离为 ,求圆M的方程. 1. 在圆(x+1)2+(y+2)2=8上到直线x+y+1=0的距离为 的点有_____个.
2. 在(x+1)2+(y-1)2=r2的圆上是否存在四个点到直线AB:3x-4y-3=0的距离等于1.3r>3五、课后训练4.求经过点M(3,-1) ,且与圆
切于点N(1,2)的圆的方程。yOCMNGxD5.设定点M(-3,4),动点N在圆x2+y2=4上运动,以OM、ON为两边作平行四边形MONP,求点P的轨迹.
