人教A版高中数学选修2-1 2.2椭圆的定义及其标准方程 课件 共27张PPT
文档属性
| 名称 | 人教A版高中数学选修2-1 2.2椭圆的定义及其标准方程 课件 共27张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 408.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-11 18:13:05 | ||
图片预览








文档简介
课件27张PPT。椭圆的定义与标准方程(2) 一、复习回顾①当常数小于两定点间的距离时②当常数等于两定点间的距离时③当常数大于两定点间的距离时没有任何曲线.两定点之间的线段.轨迹为椭圆.分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
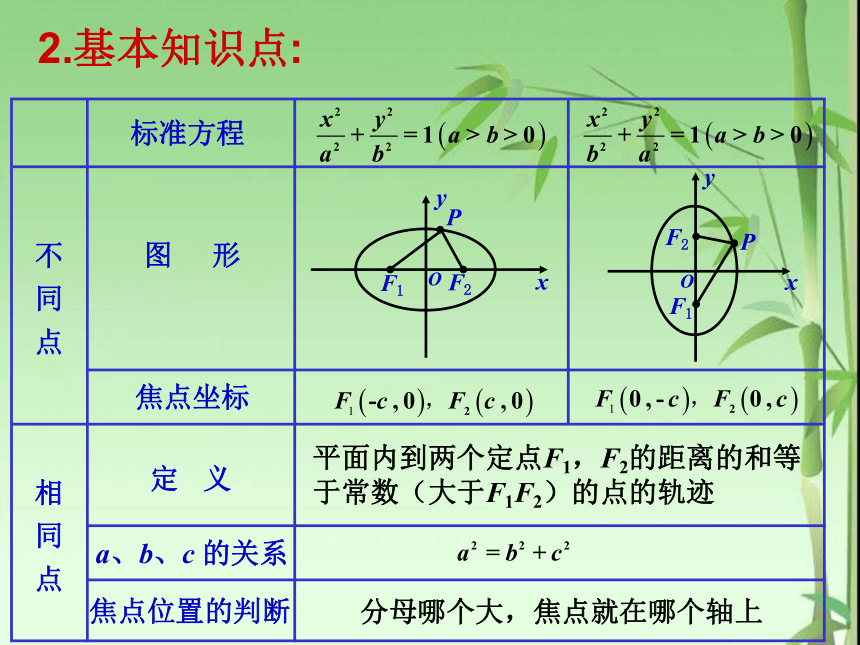
于常数(大于F1F2)的点的轨迹 2.基本知识点: Y3.椭圆的标准方程的特点:(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1(2)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。(3)由椭圆的标准方程可以求出三个参数a、b、c的值。(4)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪一个轴上。注:二、基础练习 C 2.椭圆的焦点坐标为(4,0),(-4,0),椭圆上一点到两焦点的距离之和为10,则椭圆的标准方程为( )B3、命题p:动点M到两定点A?B的距离之和|MA|+|MB|=2a(a>0,常数);命题q:动点M的轨迹是椭圆,则p是q的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件BB5、已知a=4,c=3,焦点在y轴上的椭圆的标准方程为________.6、椭圆9x2+4y2=36的焦距等于________,焦点坐标为F1________,F2________.若P为椭圆上任意一点,则|PF1|+|PF2|=________. 6 例1. 求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(-3,0),(3,0),椭圆上任意一点与两焦点的距离的和等于8;解:(1)椭圆的焦点在x轴上,设它的标准方程是由已知,得2a=8,即a=4,又因为c=3,
所以b2=a2-c2=7,因此椭圆的标准方程是 三、例题解析解:(2)椭圆的焦点在y轴上,设它的标准方程是 由已知,得c=4,因为c2=a2-b2,
所以a2=b2+16 ①将①代入②得, 解得b2=4 (b2=-12舍去),则a2=4+16=20,因此椭圆的标准方程是 解:(1)已知方程就是椭圆的标准方程,由36>24,可知这个椭圆的焦点在x轴上,且a2=36,b2=24,所以c2=a2-b2=12, 解:(2)把已知方程化为标准方程,
由8>3可知这个椭圆的解得在y轴上,
且a2=8,b2=3,得c2=a2-b2=5,(2)8x2+3y2=24.例3. 已知B,C是两个定点,|BC|=8,且△ABC的周长等于18,求这个三角形的顶点A的轨迹方程。解:以过B,C两点的直线为x轴,线段BC的垂直平分线为y轴,建立直角坐标系xOy,
由|BC|=8,可知B(-4,0),C(4,0),由|AB|+|AC|+|BC|=18,得|AB|+|AC|=10,因此点A的轨迹是以B,C为焦点的椭圆, 这个椭圆上的点与两焦点的距离的和2a=10,但A点不在x轴上, 由a=5,c=4,解得b2=9,因此点A的轨迹方程是 例4.如果方程x2+ky2=2表示焦点在y轴上的椭圆,则k的取值范围是 。解:将方程整理成 根据题意得 解得0(1)求△AF1B的周长;
(2)如果AB不垂直于x轴,△AF1B的周长有变化吗?为什么?(1) |AF1|+|AB|+|BF1|=20. (2)周长不变 如图:求满足下列条件的椭圆方程解:椭圆具有标准方程其中因此所求方程为例6. 求出刚才在实验中画出的椭圆的标准方程1.椭圆 上一点P到一个焦点的距离为5,则P点到另一个焦点的距离是( )
(A)5 (B)6 (C)4 (D)12A四、巩固练习2.椭圆 的左、右焦点为F1,F2,一直线过F1交椭圆于A、B两点,则△ABF2的周长为( )
(A)32 (B)16
(C)8 (D)4B3.若△ABC的两个顶点坐标为A(-4,0),B(4,0),△ABC的周长为18,则顶点C的轨迹方程为( )
(A) (B)
(C) (D)D粘在小页P9上方法技巧
求椭圆标准方程基本方法
(1)确定椭圆的标准方程包括“定位”和“定量”两个方面.“定位”是指确定椭圆与坐标系的相对位置,即在中心为原点的前提下,确定焦点位于哪条坐标轴上,以判断方程的形式;“定量”则是指确定a2、b2的具体数值,常用待定系数法.五、归纳小结再见!
于常数(大于F1F2)的点的轨迹 2.基本知识点: Y3.椭圆的标准方程的特点:(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1(2)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。(3)由椭圆的标准方程可以求出三个参数a、b、c的值。(4)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪一个轴上。注:二、基础练习 C 2.椭圆的焦点坐标为(4,0),(-4,0),椭圆上一点到两焦点的距离之和为10,则椭圆的标准方程为( )B3、命题p:动点M到两定点A?B的距离之和|MA|+|MB|=2a(a>0,常数);命题q:动点M的轨迹是椭圆,则p是q的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件BB5、已知a=4,c=3,焦点在y轴上的椭圆的标准方程为________.6、椭圆9x2+4y2=36的焦距等于________,焦点坐标为F1________,F2________.若P为椭圆上任意一点,则|PF1|+|PF2|=________. 6 例1. 求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(-3,0),(3,0),椭圆上任意一点与两焦点的距离的和等于8;解:(1)椭圆的焦点在x轴上,设它的标准方程是由已知,得2a=8,即a=4,又因为c=3,
所以b2=a2-c2=7,因此椭圆的标准方程是 三、例题解析解:(2)椭圆的焦点在y轴上,设它的标准方程是 由已知,得c=4,因为c2=a2-b2,
所以a2=b2+16 ①将①代入②得, 解得b2=4 (b2=-12舍去),则a2=4+16=20,因此椭圆的标准方程是 解:(1)已知方程就是椭圆的标准方程,由36>24,可知这个椭圆的焦点在x轴上,且a2=36,b2=24,所以c2=a2-b2=12, 解:(2)把已知方程化为标准方程,
由8>3可知这个椭圆的解得在y轴上,
且a2=8,b2=3,得c2=a2-b2=5,(2)8x2+3y2=24.例3. 已知B,C是两个定点,|BC|=8,且△ABC的周长等于18,求这个三角形的顶点A的轨迹方程。解:以过B,C两点的直线为x轴,线段BC的垂直平分线为y轴,建立直角坐标系xOy,
由|BC|=8,可知B(-4,0),C(4,0),由|AB|+|AC|+|BC|=18,得|AB|+|AC|=10,因此点A的轨迹是以B,C为焦点的椭圆, 这个椭圆上的点与两焦点的距离的和2a=10,但A点不在x轴上, 由a=5,c=4,解得b2=9,因此点A的轨迹方程是 例4.如果方程x2+ky2=2表示焦点在y轴上的椭圆,则k的取值范围是 。解:将方程整理成 根据题意得 解得0
(2)如果AB不垂直于x轴,△AF1B的周长有变化吗?为什么?(1) |AF1|+|AB|+|BF1|=20. (2)周长不变 如图:求满足下列条件的椭圆方程解:椭圆具有标准方程其中因此所求方程为例6. 求出刚才在实验中画出的椭圆的标准方程1.椭圆 上一点P到一个焦点的距离为5,则P点到另一个焦点的距离是( )
(A)5 (B)6 (C)4 (D)12A四、巩固练习2.椭圆 的左、右焦点为F1,F2,一直线过F1交椭圆于A、B两点,则△ABF2的周长为( )
(A)32 (B)16
(C)8 (D)4B3.若△ABC的两个顶点坐标为A(-4,0),B(4,0),△ABC的周长为18,则顶点C的轨迹方程为( )
(A) (B)
(C) (D)D粘在小页P9上方法技巧
求椭圆标准方程基本方法
(1)确定椭圆的标准方程包括“定位”和“定量”两个方面.“定位”是指确定椭圆与坐标系的相对位置,即在中心为原点的前提下,确定焦点位于哪条坐标轴上,以判断方程的形式;“定量”则是指确定a2、b2的具体数值,常用待定系数法.五、归纳小结再见!
