人教A版数学选修2-1课件:第二章 2.3双曲线及其标准方程 共20张PPT
文档属性
| 名称 | 人教A版数学选修2-1课件:第二章 2.3双曲线及其标准方程 共20张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 397.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-11 18:14:51 | ||
图片预览






文档简介
课件20张PPT。1椭圆 定义:
图形:
标准方程:
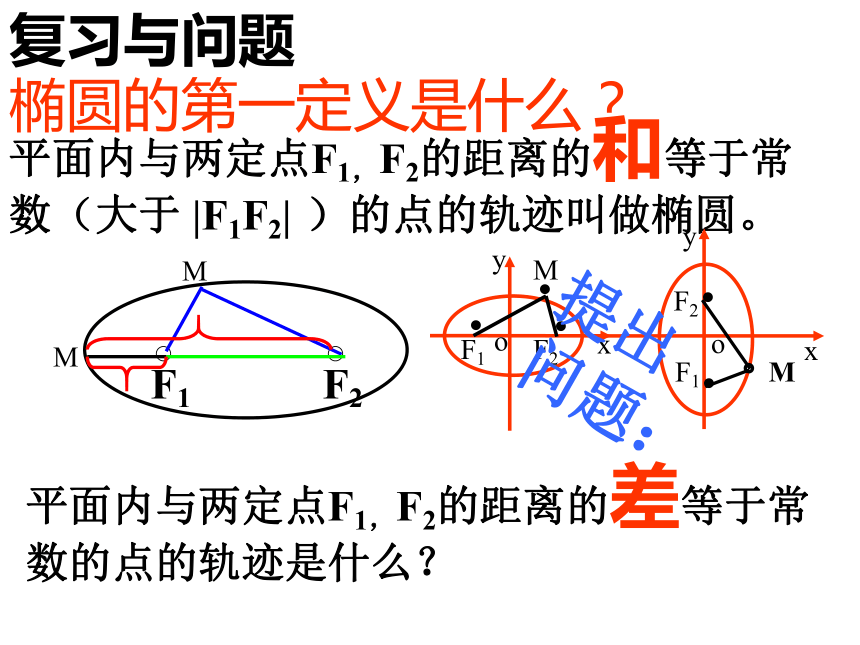
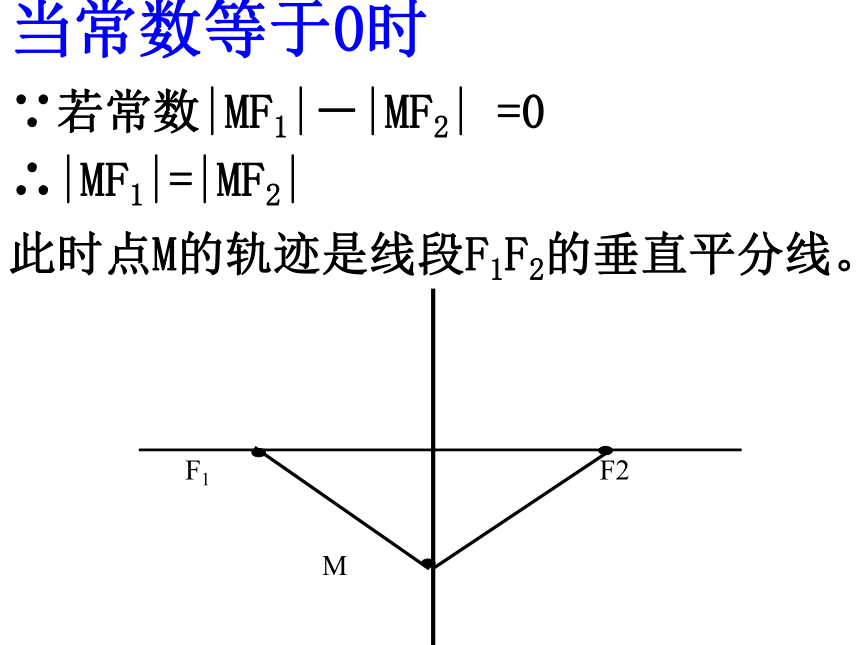
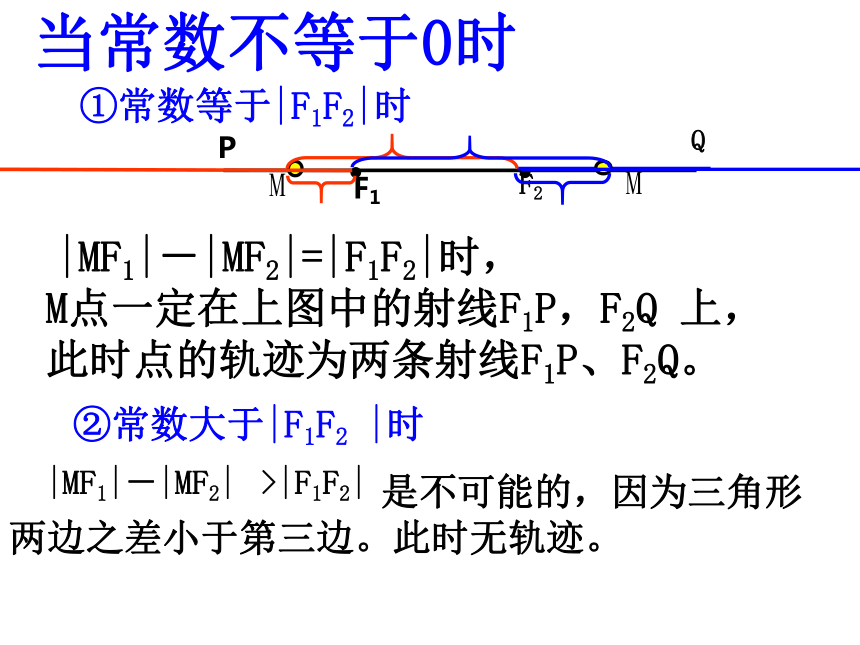
12.3.1双曲线及其标准方程(一)复习与问题椭圆的第一定义是什么?平面内与两定点F1,F2的距离的和等于常数(大于 |F1F2| )的点的轨迹叫做椭圆。F1F2M平面内与两定点F1,F2的距离的差等于常数的点的轨迹是什么?提出问题:此时点M的轨迹是线段F1F2的垂直平分线。∴|MF1|=|MF2|当常数等于0时∵若常数|MF1|-|MF2| =0当常数不等于0时①常数等于|F1F2|时PMQM |MF1|-|MF2|=|F1F2|时,
M点一定在上图中的射线F1P,F2Q 上,
此时点的轨迹为两条射线F1P、F2Q。 是不可能的,因为三角形两边之差小于第三边。此时无轨迹。②常数大于|F1F2 |时即:|MF1|-|MF2|=常数<|F1F2|① |MF1|-|MF2|>0|MF1|>|MF2|② |MF1|-|MF2|<0|MF1|<|MF2|③常数小于|F1F2 |时即:|MF1|-|MF2|=常数<|F1F2|即:|MF2|-|MF1|=常数<|F1F2|1探求结果: 平面内到两个定点F1、F2的距离的差的绝对值等于常数2a的动点的轨迹是怎样的图形?几何画板探究1已知A(-4,0) B(4,0) ,点P满足的条件分别指出点 P 的轨迹:(2)双曲线左支(1)双曲线右支(4)以B为端点的一条射线(3)以A为端点的一条射线(5,6,8)无轨迹(9)线段AB(7)以A.B为焦点的双曲线(10)以A.B为焦点的椭圆(11)线段AB的垂直平分线 11如何建立适当的直角坐标系?原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)? 探讨建立平面直角坐标系的方案方案一(对称、“简洁”)12.设点:设M(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)
常数=2a双曲线方程的推导14.化简.3.列式:1双曲线的标准方程方案一1问题:如何判断双曲线的焦点在哪个轴上?(二次项系数为正,焦点在相应的轴上)1例1:如果方程 表示双曲线,求m的取值范围.解:1| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F(0, ± c)谁正谁对应a1|MF1|+|MF2|=2a(2a>|F1F2|)a2=b2+c2F ( ±c,0) F(0, ± c)
x谁大谁对应a12. y2-2x2=1的焦点为 、焦距是 .练习巩固:1方程表示的曲线是双曲线方程表示的曲线是双曲线的右支方程表示的曲线是x轴上分别以F1和F2为端点,
指向x轴的负半轴和正半轴的两条射线。练习巩固:
图形:
标准方程:
12.3.1双曲线及其标准方程(一)复习与问题椭圆的第一定义是什么?平面内与两定点F1,F2的距离的和等于常数(大于 |F1F2| )的点的轨迹叫做椭圆。F1F2M平面内与两定点F1,F2的距离的差等于常数的点的轨迹是什么?提出问题:此时点M的轨迹是线段F1F2的垂直平分线。∴|MF1|=|MF2|当常数等于0时∵若常数|MF1|-|MF2| =0当常数不等于0时①常数等于|F1F2|时PMQM |MF1|-|MF2|=|F1F2|时,
M点一定在上图中的射线F1P,F2Q 上,
此时点的轨迹为两条射线F1P、F2Q。 是不可能的,因为三角形两边之差小于第三边。此时无轨迹。②常数大于|F1F2 |时即:|MF1|-|MF2|=常数<|F1F2|① |MF1|-|MF2|>0|MF1|>|MF2|② |MF1|-|MF2|<0|MF1|<|MF2|③常数小于|F1F2 |时即:|MF1|-|MF2|=常数<|F1F2|即:|MF2|-|MF1|=常数<|F1F2|1探求结果: 平面内到两个定点F1、F2的距离的差的绝对值等于常数2a的动点的轨迹是怎样的图形?几何画板探究1已知A(-4,0) B(4,0) ,点P满足的条件分别指出点 P 的轨迹:(2)双曲线左支(1)双曲线右支(4)以B为端点的一条射线(3)以A为端点的一条射线(5,6,8)无轨迹(9)线段AB(7)以A.B为焦点的双曲线(10)以A.B为焦点的椭圆(11)线段AB的垂直平分线 11如何建立适当的直角坐标系?原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)? 探讨建立平面直角坐标系的方案方案一(对称、“简洁”)12.设点:设M(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)
常数=2a双曲线方程的推导14.化简.3.列式:1双曲线的标准方程方案一1问题:如何判断双曲线的焦点在哪个轴上?(二次项系数为正,焦点在相应的轴上)1例1:如果方程 表示双曲线,求m的取值范围.解:1| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F(0, ± c)谁正谁对应a1|MF1|+|MF2|=2a(2a>|F1F2|)a2=b2+c2F ( ±c,0) F(0, ± c)
x谁大谁对应a12. y2-2x2=1的焦点为 、焦距是 .练习巩固:1方程表示的曲线是双曲线方程表示的曲线是双曲线的右支方程表示的曲线是x轴上分别以F1和F2为端点,
指向x轴的负半轴和正半轴的两条射线。练习巩固:
