20.1.2 中位数和众数(3)课件
图片预览






文档简介
人教版数学八年级下册
20.1.2中位数与众数(3)
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。
什么叫中位数?
中位数的作用:
中位数也是用来描述数据的集中趋势的,中位数是一个位置代表值。如果已知一组数据的中位数,那么可以知道,小于等于或大于等于这个中位数的数据各占一半。
众数也常作为一组数据的代表,用来描述数据的集中趋势。当一组数据有较多的重复数据时,众数往往是人们所关心的一个量。
众数的作用:
一组数据中出现次数最多的数据就是这组数据的众数。
什么叫众数?
平均数、中位数、众数三者有什么联系与区别?
联系:它们从不同角度描述了一组数据的集中趋势。
1.平均数——计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值的影响。它应用最为广泛。
区别:
2.中位数——中位数的优点是计算简单,不受极端值的影响,只与其在数据中的位置有关,但不能充分利用所有的数据信息。
3.众数——众数不受极端值的影响, 但不能充分利用所有的数据信息,而且当各个数据的重复次数大致相等时,众数往往没有特别的意义。
鞋店老板一般最关心_____
公司老板一般以_____为销售标准
裁判一般以______为选手最终得分
众数
中位数
平均数
平均数、中位数和众数都可以作为一组数据的代表,它们各有自己的特点,能够从不同的角度提供信息。
在实际应用中,需要分析具体问题的情况,选择适当的量来代表数据。
比如:
你认为哪一个
同学的成绩最好呢?
说明理由.
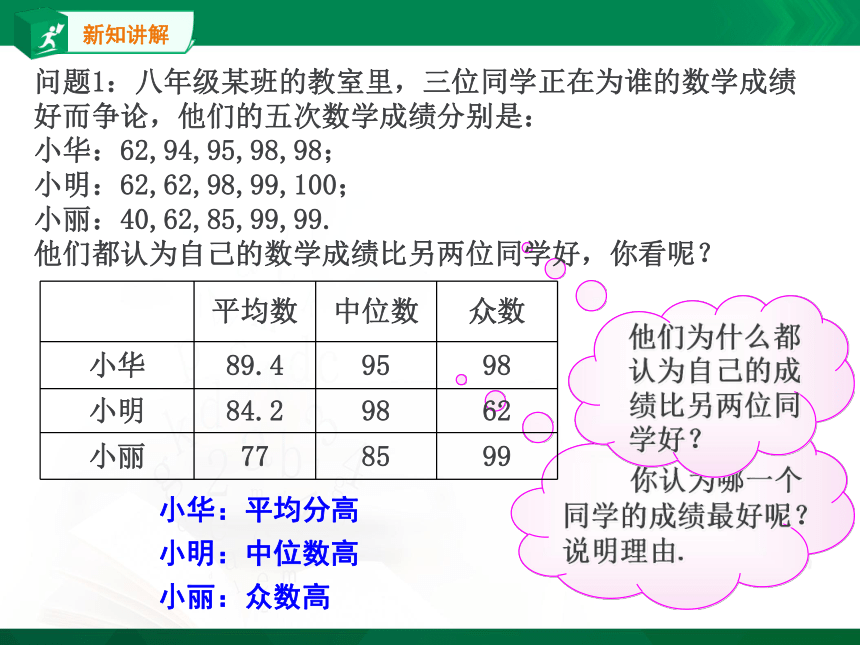
问题1:八年级某班的教室里,三位同学正在为谁的数学成绩好而争论,他们的五次数学成绩分别是:
小华:62,94,95,98,98;
小明:62,62,98,99,100;
小丽:40,62,85,99,99.
他们都认为自己的数学成绩比另两位同学好,你看呢?
小华:平均分高
小明:中位数高
小丽:众数高
平均数 中位数 众数
小华 89.4 95 98
小明 84.2 98 62
小丽 77 85 99
问题2:某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成情况对营业员进行适当的奖惩.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元) ,数据如下:(结果保留整数)
18 16 13 24 15 28 26 18 19
17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
(1)月销售额在哪个值的人数最多?中间的销售额是多少?平均的月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
解:(1)分析数据:样本中,15出现的次数最多;故样本众数为15,所以月销售额在15万元人数最多; 将数据从小到大排列,找最中间的两个数都为18,故中位数是18,所以中间的月销售额是18万元; 根据平均数的求法,平均数为(17+18+16+13+24+15+…+28+28+16+19)÷30≈20.
故这组数据的平均数约是20,所以平均的月销售额是20万元.
(3)如果想让一半左右的营业员都能达到目标,月销售额可以定为18万元(中位数),因为从样本情况看,月销售额在18万元以上(含18万元)的有15人,占总人数的一半左右,可以估计,每月销售额定为18万元,可以估计一半左右的营业员获得奖励.
问题3:甲、乙两名运动员在6次百米跑训练中的成绩如下:
请你比较这两组数据的众数,平均数和中位数,再作判断。
分析:谈看法实质上就是按众数,平均数和中位数的大小比较其优劣。
解:甲的平均数10.9,众数10.8,中位数10.85;乙的平均数10.8,众数10.9,中位数10.85。
从平均数看:甲的成绩比乙的好,从众数看:乙的成绩比甲的好,从中位数看两人成绩一样。
甲(秒) 10.8 10.9 11.0 10.7 11.2 10.8
乙(秒) 10.9 10.9 10.8 10.8 10.5 10.9
1. 知识小结:我们学习了众数、中位数的概念,了解了它们在描述一组数据“平均水平” 时的不同角度和适用范围。
2.方法小结:①众数由所给数据可直接求出,(一组数据中的众数可能不止一个,众数是一组数据中出现的次数最多的数据,而不是该数据出现的次数.如果有两个数据出现的次数相同,并且比其他数据出现次数都多,那么这两个数据都是这组数据的众数)。
②求中位数时,首先要先排序(从小到大或从大到小),然后计算中位数的序号,分数据为奇数个与偶数个两种来求.(既找出最中间的一个数据或最中间两个数并算出它们的平均数)。
3.知识网络:平均数、众数及中位数都是描述一组数据的集中趋势的特征数,但描述的角度和适用范围有所不同。平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动;众数着眼于对各数据出现的频数的考察,其大小只与这组数据中的部分数据有关。当一组数据中有不少数据多次重复出现时,其众数往往是我们关心的一种统计量;中位数则仅与数据的排列位置有关,某些数据的变动对它的中位数没有影响。当一组数据中的个别数据变动较大时,可用它来描述其集中趋势。
年收入 (万元)
所占户数比
1.某同学进行社会调查,随机抽查某地区20个家庭的收入情况,并绘制了统计图请根据统计图给出的信息回答:
(1)填写下表:
这20个家庭的年平均收入为————万元。
(2)数据中的中位数是————万元,众数是————万元。
1
1
2
3
4
5
3
1
1.6
1.2
1.3
年收入(万元) 0.6 0.9 1.0 1.1 1.2 1.3 1.4 9.7
家庭户数
2.某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月销售量如下:
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)假定销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你给出一个较合理的销售定额。
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
解:(1)平均数:320件,众数210件,中位数:210件。
(2)不合理。因为15人中只有2个销售额超过了320件,而有13人达不到320件,尽管320件是平均数,但它却不能反映营销人员的一般水平,销售额定为210件更合适,因为210既是众数,又是中位数,是大部分人都能达到的定额。
3.在某次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示:
分别求这些运动员成绩的众数、中位数与平均数(平均数保留两位小数)并解释所求结果的实际意义。
成绩(米) 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3
2 3 4 1 1 1
解:在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75;上表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,,即这组数据的中位数是1.70;这组数据的平均数是1.69米。
运动员成绩的众数是1.75米,说明成绩为1.75米的人数最多;运动员成绩的中位数是1.70米,说明1.70米以下和1.70米以上的数据各占一半;运动员成绩的平均数是1.69米,说明所有参赛运动员的平均成绩是1.69米。
课本P122习题20.1第6题、第7题。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
20.1.2中位数与众数(3)
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。
什么叫中位数?
中位数的作用:
中位数也是用来描述数据的集中趋势的,中位数是一个位置代表值。如果已知一组数据的中位数,那么可以知道,小于等于或大于等于这个中位数的数据各占一半。
众数也常作为一组数据的代表,用来描述数据的集中趋势。当一组数据有较多的重复数据时,众数往往是人们所关心的一个量。
众数的作用:
一组数据中出现次数最多的数据就是这组数据的众数。
什么叫众数?
平均数、中位数、众数三者有什么联系与区别?
联系:它们从不同角度描述了一组数据的集中趋势。
1.平均数——计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值的影响。它应用最为广泛。
区别:
2.中位数——中位数的优点是计算简单,不受极端值的影响,只与其在数据中的位置有关,但不能充分利用所有的数据信息。
3.众数——众数不受极端值的影响, 但不能充分利用所有的数据信息,而且当各个数据的重复次数大致相等时,众数往往没有特别的意义。
鞋店老板一般最关心_____
公司老板一般以_____为销售标准
裁判一般以______为选手最终得分
众数
中位数
平均数
平均数、中位数和众数都可以作为一组数据的代表,它们各有自己的特点,能够从不同的角度提供信息。
在实际应用中,需要分析具体问题的情况,选择适当的量来代表数据。
比如:
你认为哪一个
同学的成绩最好呢?
说明理由.
问题1:八年级某班的教室里,三位同学正在为谁的数学成绩好而争论,他们的五次数学成绩分别是:
小华:62,94,95,98,98;
小明:62,62,98,99,100;
小丽:40,62,85,99,99.
他们都认为自己的数学成绩比另两位同学好,你看呢?
小华:平均分高
小明:中位数高
小丽:众数高
平均数 中位数 众数
小华 89.4 95 98
小明 84.2 98 62
小丽 77 85 99
问题2:某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成情况对营业员进行适当的奖惩.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元) ,数据如下:(结果保留整数)
18 16 13 24 15 28 26 18 19
17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
(1)月销售额在哪个值的人数最多?中间的销售额是多少?平均的月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
解:(1)分析数据:样本中,15出现的次数最多;故样本众数为15,所以月销售额在15万元人数最多; 将数据从小到大排列,找最中间的两个数都为18,故中位数是18,所以中间的月销售额是18万元; 根据平均数的求法,平均数为(17+18+16+13+24+15+…+28+28+16+19)÷30≈20.
故这组数据的平均数约是20,所以平均的月销售额是20万元.
(3)如果想让一半左右的营业员都能达到目标,月销售额可以定为18万元(中位数),因为从样本情况看,月销售额在18万元以上(含18万元)的有15人,占总人数的一半左右,可以估计,每月销售额定为18万元,可以估计一半左右的营业员获得奖励.
问题3:甲、乙两名运动员在6次百米跑训练中的成绩如下:
请你比较这两组数据的众数,平均数和中位数,再作判断。
分析:谈看法实质上就是按众数,平均数和中位数的大小比较其优劣。
解:甲的平均数10.9,众数10.8,中位数10.85;乙的平均数10.8,众数10.9,中位数10.85。
从平均数看:甲的成绩比乙的好,从众数看:乙的成绩比甲的好,从中位数看两人成绩一样。
甲(秒) 10.8 10.9 11.0 10.7 11.2 10.8
乙(秒) 10.9 10.9 10.8 10.8 10.5 10.9
1. 知识小结:我们学习了众数、中位数的概念,了解了它们在描述一组数据“平均水平” 时的不同角度和适用范围。
2.方法小结:①众数由所给数据可直接求出,(一组数据中的众数可能不止一个,众数是一组数据中出现的次数最多的数据,而不是该数据出现的次数.如果有两个数据出现的次数相同,并且比其他数据出现次数都多,那么这两个数据都是这组数据的众数)。
②求中位数时,首先要先排序(从小到大或从大到小),然后计算中位数的序号,分数据为奇数个与偶数个两种来求.(既找出最中间的一个数据或最中间两个数并算出它们的平均数)。
3.知识网络:平均数、众数及中位数都是描述一组数据的集中趋势的特征数,但描述的角度和适用范围有所不同。平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动;众数着眼于对各数据出现的频数的考察,其大小只与这组数据中的部分数据有关。当一组数据中有不少数据多次重复出现时,其众数往往是我们关心的一种统计量;中位数则仅与数据的排列位置有关,某些数据的变动对它的中位数没有影响。当一组数据中的个别数据变动较大时,可用它来描述其集中趋势。
年收入 (万元)
所占户数比
1.某同学进行社会调查,随机抽查某地区20个家庭的收入情况,并绘制了统计图请根据统计图给出的信息回答:
(1)填写下表:
这20个家庭的年平均收入为————万元。
(2)数据中的中位数是————万元,众数是————万元。
1
1
2
3
4
5
3
1
1.6
1.2
1.3
年收入(万元) 0.6 0.9 1.0 1.1 1.2 1.3 1.4 9.7
家庭户数
2.某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月销售量如下:
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)假定销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你给出一个较合理的销售定额。
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
解:(1)平均数:320件,众数210件,中位数:210件。
(2)不合理。因为15人中只有2个销售额超过了320件,而有13人达不到320件,尽管320件是平均数,但它却不能反映营销人员的一般水平,销售额定为210件更合适,因为210既是众数,又是中位数,是大部分人都能达到的定额。
3.在某次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示:
分别求这些运动员成绩的众数、中位数与平均数(平均数保留两位小数)并解释所求结果的实际意义。
成绩(米) 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3
2 3 4 1 1 1
解:在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75;上表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,,即这组数据的中位数是1.70;这组数据的平均数是1.69米。
运动员成绩的众数是1.75米,说明成绩为1.75米的人数最多;运动员成绩的中位数是1.70米,说明1.70米以下和1.70米以上的数据各占一半;运动员成绩的平均数是1.69米,说明所有参赛运动员的平均成绩是1.69米。
课本P122习题20.1第6题、第7题。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
