湘教版数学八年级下册4.1.1 函数和它的表示方法 课件 (共21张PPT)
文档属性
| 名称 | 湘教版数学八年级下册4.1.1 函数和它的表示方法 课件 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 810.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-11 19:31:47 | ||
图片预览








文档简介
课件21张PPT。第四章 一次函数
1 函数 学习目标1、在具体情境中理解什么是变量、自变量、因变量。
2、能从表格中获得变量之间关系的信息,能用表格表示变量之间的关系,尝试对变化趋势进行初步的预测。
3、经历观察、实验、猜想、验证等数学活动,发展合理推理能力,并能有条理地、清晰地阐述自己的观点。
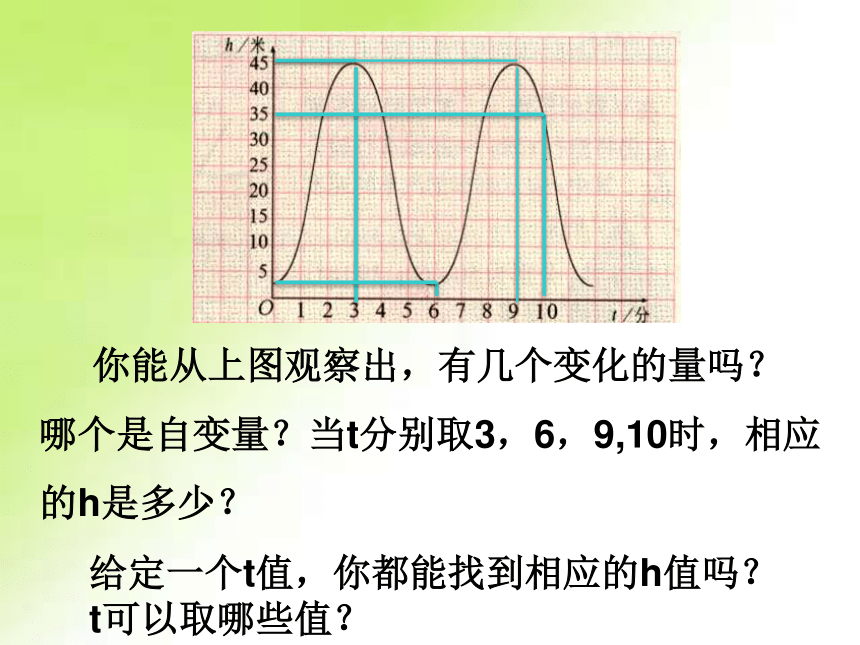
七年级我们已经学习了《变量之间的关系》知道生活中有许许多多变化的量。什么是变量?你了解这些变量之间的关系吗?如何刻画这些变量之间的关系呢?现在就让我们和洋葱仔一起温习温习吧温故而知新 刚才司机师傅通过自己的经验告诉我们,打车的时候有两个变量,就是 . 和 ,常量就是在打车距离和费用这个变化关系里不变的量,比如起步价和每公里的价格。行驶的距离产生的费用 一个变化过程中有两个变量一个是主动变化的咱叫它. 另一个因为 变了,它才跟着变化的就是 ,那么在上个变化关系里 是自变量, . 是因变量因变量自变量自变量行驶距离产生的费用崂山山清水秀,10.1洋葱仔打车来咱崂山游玩,细心的仔仔发现汽车仪表盘上显示的行驶公里数和油表盘上显示的余油量有一种关系,仔仔随手记录了一些数据。观察表格并说说这两个变量哪个是自变量?哪个是因变量?给定一个X值能确定几个P的值?自变量可以取哪些值?师生合作,探究新知仔仔很开心,坐上了颇有挑战摩天轮崂山的风景真是美当人坐在摩天轮上时,人的高度随时间在变化,那么变化有规律吗?摩天轮上一点的高度h与旋转时间t之间有一定的关系,右图就反映了时间t(分)与摩天轮上一点的高度h(米)之间的关系. 你能从上图观察出,有几个变化的量吗?哪个是自变量?当t分别取3,6,9,10时,相应的h是多少?给定一个t值,你都能找到相应的h值吗?t可以取哪些值?游玩了一天,仔仔打车回家。幽默的司机师傅得知仔仔是8.3的学生,于是就跟他开了个玩笑,说:“我的计价器坏了,但我的仪表盘可以计算你行驶的路程并且我这儿有个计费公式Y=13+2.3(X-3),你自己算算该给我多少钱?算少了,我可不依,算多了,我可不退哦。(起步费13元,3公里后,每公里加价2.3元)在这个式子中有哪几个变量?X能取哪些值?给X一个值有几个Y值与之对应? 在上面的问题中,都有两个变量,给定其中一个变量(自变量)的值,相应地就确定了另一个变量(因变量)的值. 一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.以上三个问题有什么共同点吗?关键词:两个变量 ,一个x值确定一个y值你理解了吗?
第一个问题中 是 的函数
第二个问题中 是 的函数
第三个问题中 是 的函数议一议在上面我们研究的三个问题相同点:都研究了两个变量,并且其中一个变量是另一个变量的函数.上面三个问题又有哪些不同点?不同点:表现形式不同。在第一个问题中,是以表格的形式表示两个变量之间的关系,第二个问题中是以图像的形式表示两个变量之间的关系,第三个问题是以关系表达式的形式表示两个变量之间的关系. 函数常用的三种表示方法:
(1)图象法 (2)列表法 (3)解析法生生合作,巩固练习瓶子或罐头盒等圆柱形的物体,常常如下图这样堆放。随着层数的增加,物体的总数是如何变化的?15106311510631在这个变化过程,有哪几个变量?其中谁是自变量?给定一个n值能确定几个y的值?物体总数y是层数n的函数吗?自变量可以取哪些值?如图是某物体的抛射曲线图,其中s表示物体与抛射点之间的水平距离,h表示物体的高度
这个图象反映了哪两个变量之间的关系?
根据图象填表当距离s取0米至6米之间的一个确定的值时,相应的高度h确定吗?
高度h可以看成距离s的函数吗?一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)在这个关系里有几个变量?
(2)当t分别等于-43,-27,0,18时,相应的热力学温度T是多少?
(3)给定一个大于-273 ℃的t值,你能求出相应的T值吗?一个t值能确定几个T值?
(4)热力学温度T可以看做是摄氏温度t的函数吗?反思突破如何判断一个变化关系是否是函数?(1)两个变量
(2)一个自变量X的值确定 一个因变量Y的值 小明骑车从家到学校速度是15千米/时,你能表示出他走过的路程s与时间t之间的变化关系吗?S=15t 路程s随时间t的变化的图象是什么?你明白了吗?S是t的函数吗?S是t的函数 若正方形的边长为x,则面积y与边长x之间的关系是什么? 面积y随边长x的变化的图象是什么?面积问题y=x2x你理解“函数”了吗?y是x的函数吗?y是x的函数小试牛刀2
下列各式中,x都是自变量,则y是不是x的函数,为什么?1. y= x2 +3
2. y2=x+3
1 函数 学习目标1、在具体情境中理解什么是变量、自变量、因变量。
2、能从表格中获得变量之间关系的信息,能用表格表示变量之间的关系,尝试对变化趋势进行初步的预测。
3、经历观察、实验、猜想、验证等数学活动,发展合理推理能力,并能有条理地、清晰地阐述自己的观点。
七年级我们已经学习了《变量之间的关系》知道生活中有许许多多变化的量。什么是变量?你了解这些变量之间的关系吗?如何刻画这些变量之间的关系呢?现在就让我们和洋葱仔一起温习温习吧温故而知新 刚才司机师傅通过自己的经验告诉我们,打车的时候有两个变量,就是 . 和 ,常量就是在打车距离和费用这个变化关系里不变的量,比如起步价和每公里的价格。行驶的距离产生的费用 一个变化过程中有两个变量一个是主动变化的咱叫它. 另一个因为 变了,它才跟着变化的就是 ,那么在上个变化关系里 是自变量, . 是因变量因变量自变量自变量行驶距离产生的费用崂山山清水秀,10.1洋葱仔打车来咱崂山游玩,细心的仔仔发现汽车仪表盘上显示的行驶公里数和油表盘上显示的余油量有一种关系,仔仔随手记录了一些数据。观察表格并说说这两个变量哪个是自变量?哪个是因变量?给定一个X值能确定几个P的值?自变量可以取哪些值?师生合作,探究新知仔仔很开心,坐上了颇有挑战摩天轮崂山的风景真是美当人坐在摩天轮上时,人的高度随时间在变化,那么变化有规律吗?摩天轮上一点的高度h与旋转时间t之间有一定的关系,右图就反映了时间t(分)与摩天轮上一点的高度h(米)之间的关系. 你能从上图观察出,有几个变化的量吗?哪个是自变量?当t分别取3,6,9,10时,相应的h是多少?给定一个t值,你都能找到相应的h值吗?t可以取哪些值?游玩了一天,仔仔打车回家。幽默的司机师傅得知仔仔是8.3的学生,于是就跟他开了个玩笑,说:“我的计价器坏了,但我的仪表盘可以计算你行驶的路程并且我这儿有个计费公式Y=13+2.3(X-3),你自己算算该给我多少钱?算少了,我可不依,算多了,我可不退哦。(起步费13元,3公里后,每公里加价2.3元)在这个式子中有哪几个变量?X能取哪些值?给X一个值有几个Y值与之对应? 在上面的问题中,都有两个变量,给定其中一个变量(自变量)的值,相应地就确定了另一个变量(因变量)的值. 一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.以上三个问题有什么共同点吗?关键词:两个变量 ,一个x值确定一个y值你理解了吗?
第一个问题中 是 的函数
第二个问题中 是 的函数
第三个问题中 是 的函数议一议在上面我们研究的三个问题相同点:都研究了两个变量,并且其中一个变量是另一个变量的函数.上面三个问题又有哪些不同点?不同点:表现形式不同。在第一个问题中,是以表格的形式表示两个变量之间的关系,第二个问题中是以图像的形式表示两个变量之间的关系,第三个问题是以关系表达式的形式表示两个变量之间的关系. 函数常用的三种表示方法:
(1)图象法 (2)列表法 (3)解析法生生合作,巩固练习瓶子或罐头盒等圆柱形的物体,常常如下图这样堆放。随着层数的增加,物体的总数是如何变化的?15106311510631在这个变化过程,有哪几个变量?其中谁是自变量?给定一个n值能确定几个y的值?物体总数y是层数n的函数吗?自变量可以取哪些值?如图是某物体的抛射曲线图,其中s表示物体与抛射点之间的水平距离,h表示物体的高度
这个图象反映了哪两个变量之间的关系?
根据图象填表当距离s取0米至6米之间的一个确定的值时,相应的高度h确定吗?
高度h可以看成距离s的函数吗?一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)在这个关系里有几个变量?
(2)当t分别等于-43,-27,0,18时,相应的热力学温度T是多少?
(3)给定一个大于-273 ℃的t值,你能求出相应的T值吗?一个t值能确定几个T值?
(4)热力学温度T可以看做是摄氏温度t的函数吗?反思突破如何判断一个变化关系是否是函数?(1)两个变量
(2)一个自变量X的值确定 一个因变量Y的值 小明骑车从家到学校速度是15千米/时,你能表示出他走过的路程s与时间t之间的变化关系吗?S=15t 路程s随时间t的变化的图象是什么?你明白了吗?S是t的函数吗?S是t的函数 若正方形的边长为x,则面积y与边长x之间的关系是什么? 面积y随边长x的变化的图象是什么?面积问题y=x2x你理解“函数”了吗?y是x的函数吗?y是x的函数小试牛刀2
下列各式中,x都是自变量,则y是不是x的函数,为什么?1. y= x2 +3
2. y2=x+3
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
