第19章 矩形、菱形与正方形单元检测试卷
文档属性
| 名称 | 第19章 矩形、菱形与正方形单元检测试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-12 13:40:29 | ||
图片预览



文档简介
华师大八年级下第19章 矩形、菱形与正方形单元检测试卷
班级_____________考号______________姓名_______________总分_________________
一、选择题(12小题,每题3分,共36分)
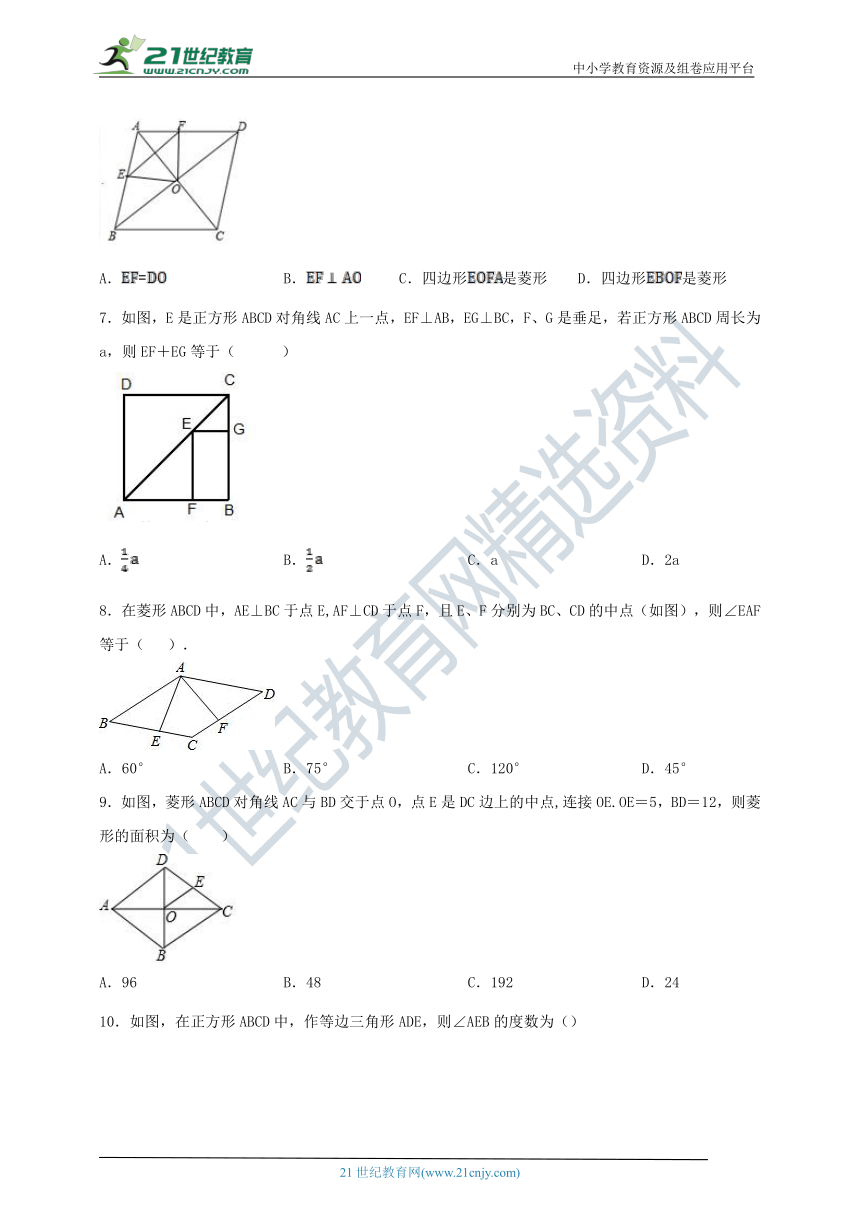
1.如图,在菱形ABCD中,∠A=130°,连接BD,∠DBC等于( )
A.25° B.35° C.50° D.65°
2.四边形的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AC=BD C.AB=BC D.AD=BC
3.如图,在长方形ABCD中,已知,,将AD沿直线AF折叠,使点D落在BC的点E处,则CF的长是
A.1cm B.2cm C.3cm D.4cm
4.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AO=4,则AB的长是( )
A.4 B.5 C.6 D.8
5.如图,在矩形中,,点,,,分别是边,,,的中点,连接,,则图中矩形的个数共有( )
A.5个 B.8个 C.9个 D.11个
6.如图,是菱形的对角线,分别是边的中点,连接,,则下列结论错误的是( )
A. B. C.四边形是菱形 D.四边形是菱形
7.如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,若正方形ABCD周长为a,则EF+EG等于( )
A. B. C.a D.2a
8.在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点(如图),则∠EAF等于( ).
A.60° B.75° C.120° D.45°
9.如图,菱形ABCD对角线AC与BD交于点O,点E是DC边上的中点,连接OE.OE=5,BD=12,则菱形的面积为( )
A.96 B.48 C.192 D.24
10.如图,在正方形ABCD中,作等边三角形ADE,则∠AEB的度数为()
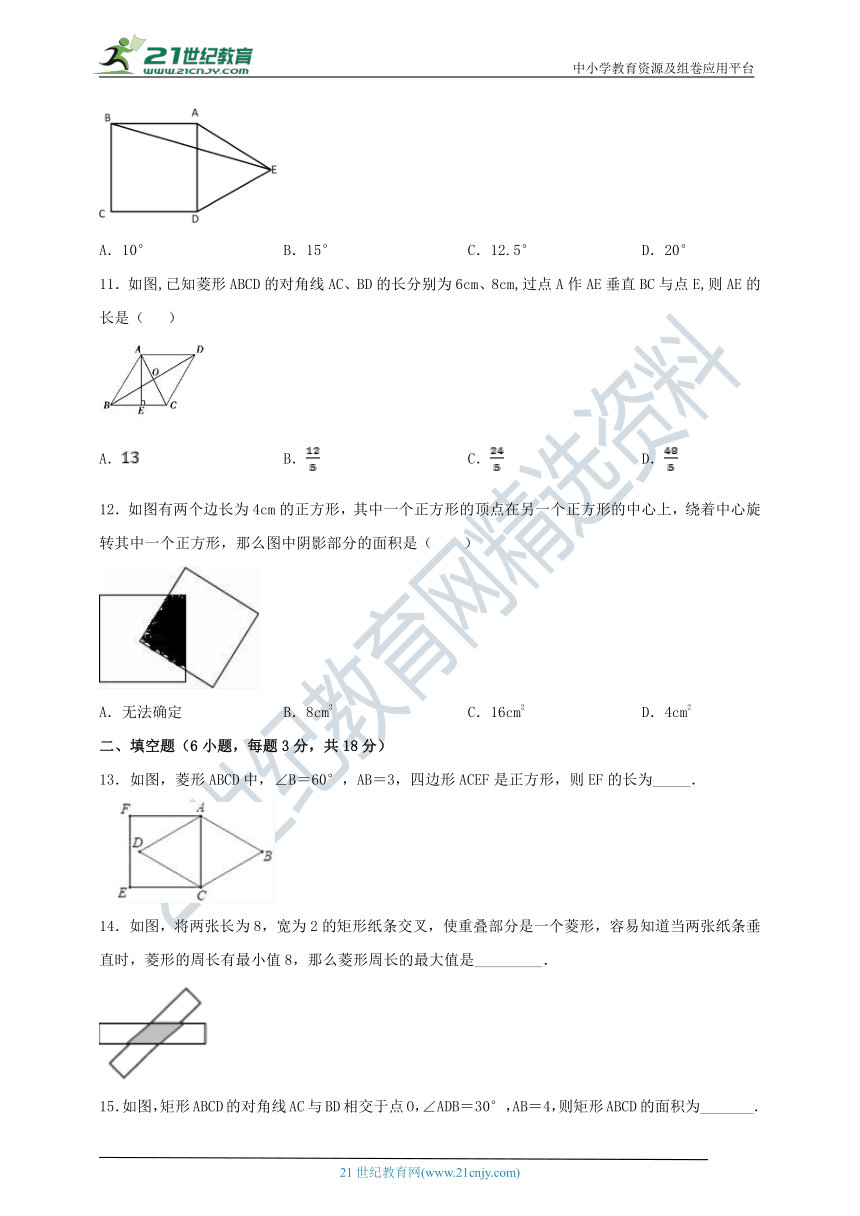
A.10° B.15° C.12.5° D.20°
11.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,过点A作AE垂直BC与点E,则AE的长是( )
A. B. C. D.
12.如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )
A.无法确定 B.8cm2 C.16cm2 D.4cm2
二、填空题(6小题,每题3分,共18分)
13.如图,菱形ABCD中,∠B=60°,AB=3,四边形ACEF是正方形,则EF的长为_____.
14.如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是_________.
15.如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则矩形ABCD的面积为_______.
16.如图,在矩形纸片中,,,边上有一点,,将纸片折叠,使点与点重合,折痕交于点,则线段的长是__.
17.如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是_____度.
18.如图,在△ABC中,AB=3+,∠B=45°,∠C=105°,点 D、E、F分别在AC、BC、AB上,且四边形ADEF为菱形,若点P是AE上一个动点,则PF+PB的最小值为___________ 。
三、解答题(8小题,共66分)
19.矩形ABCD的对角线AC、BD相交与O,DE//AC,CE//BD.求证:四边形OCED是菱形.
20.如图,在正方形ABCD中,AB=4,AE=2,DF=1,请你判定△BEF的形状,并说明理由.
21.如图,将长方形纸片ABCD沿AC翻折,点B落在点E处,连接BD,若∠1=∠3,AE∥BD,求∠EAC的度数.
22.如图,在矩形ABCD中,AF平分∠BAD交BC于E,交DC延长线于F,点G为EF的中点,连结DG.
(1)求证:BC=DF;
(2)连BD,求BD:DG的值.
23.如图,四边形中,,,于交的延长线于,,.
(1)求证:.
(2)求证:四边形是菱形.
24.如图,现将平行四边形ABCD沿其对角线AC折叠,使点B落在点B′处.AB′与CD交于点E.
(1)求证:△AED≌△CEB′;
(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.
25.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)若CE=8,CF=6,求OC的长
(3)连结AE,AF,当点O运动到何处时,四边形AECF是矩形?并说出你的理由.
26.已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
(1)若BF⊥AE,
①求证:BF=AE;
②连接OD,确定OD与AB的数量关系,并证明;
(2)若正方形的边长为4,且BF=AE,求BO的长.
参考答案
1.【考点】菱形的性质,等腰三角形的性质
【分析】直接利用菱形的性质得出∠C的度数,再利用等腰三角形的性质得出答案.
解:∵在菱形ABCD中,∠A=130°,
∴∠C=130°,BC=DC,
∴∠DBC=∠CDB=(180°-130°)=25°.
故选:A.
【点睛】此题主要考查了菱形的性质以及等腰三角形的性质,正确应用菱形的性质是解题关键.
2.【考点】矩形的判定
【分析】四边形ABCD的对角线互相平分,则说明四边形是平行四边形,由矩形的判定定理可得,只需添加条件是对角线相等.
解:可添加AC=BD,理由如下: ∵四边形ABCD的对角线互相平分, ∴四边形ABCD是平行四边形, ∵AC=BD,根据矩形判定定理对角线相等的平行四边形是矩形, ∴四边形ABCD是矩形. 故选:B.
【点睛】考查了矩形的判定,关键是矩形的判定:①矩形的定义:有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形.
3.【考点】翻折变换,矩形的性质,勾股定理
【分析】由矩形的性质和折叠的性质可得,,由勾股定理可求BE的长,即可得CE的长,再由勾股定理可求CF的长.
解:四边形ABCD是矩形,
,,
折叠
,,
在中,,
,
在中,,
故选:C.
【点睛】本题考查了翻折变换,矩形的性质,勾股定理,熟练掌握折叠的性质是本题的关键.
4.【考点】矩形的性质,等边三角形的性质和判定
【分析】根据矩形性质得出AO=OC,BO=OD,AC=BD,推出OA=OB,得出△AOB是等边三角形,推出AB=AO=4即可.
解:∵四边形ABCD是矩形,
∴AO=OC,BO=OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=4,
故选:A.
【点睛】本题考查了矩形的性质,等边三角形的性质和判定的应用;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.
5.【考点】矩形的判定
【分析】根据矩形的判定定理解答.
解:∵E,G分别是边DA,BC的中点,四边形ABCD是矩形,
∴四边形DEGC、AEGB是矩形,
同理四边形ADHF、BCHF是矩形,
则图中四个小四边形是矩形,
故图中矩形的个数共有9个,
故选:C.
【点睛】本题考查的是矩形的判定,掌握矩形的判定定理是解题的关键.
6.【考点】菱形的性质和判定,三角形的中位线定理,平行四边形的判定
【分析】根据菱形的性质和三角形的中位线以及菱形的判定可得AC⊥BD且DO=BD,再根据三角形的中位线可得EF=BD,即可得出结论
解:∵是菱形的对角线,
∴AC⊥BD且DO=BD,
∵分别是边的中点,
∴EF=BD,EF//BD,
∴EF=DO, ∴选项A正确.
∵AC⊥BD,EF//BD
∴,∴选项B正确.
∵是菱形的对角线,
∴BC=CD,O为AC的中点
∵分别是边的中点,
∴EO//BC//AD,FO//CD//AB且EO=FO=BC=DC
∴四边形是菱形∴选项C正确.
∵EF//BD,FO//AB
∴.四边形是平行四边形
∴选项D错误.
故选:D.
【点睛】本题考查了菱形的性质和判定、三角形的中位线定理、平行四边形的判定以及平行线的性质,熟练掌握相关知识是解题的关键.
7.【考点】正方形的性质,矩形的性质和判定
【分析】由正方形的性质可知∠BAC=∠ACB,又知EF⊥AB,EG⊥BC,可得EG=CG,EF=GB,从而求出EF+EG=BC即可.
解:∵E是正方形ABCD对角线AC上一点,
∴∠BAC=∠ACB=45°,∠B=90°
∵EF⊥AB,EG⊥BC,F、G是垂足,
∴四边形EFBG是矩形,三角形CGE是等腰直角三角形
∴EG=CG,EF=BG,
∴EF+EG=BC
∵正方形ABCD周长为a,
∴BC=,
∴EF+EG=,
故选:A.
【点睛】本题主要考查正方形的性质、矩形的性质和判定,利用等腰直角三角形的性质解决所求问题.
8.【考点】菱形的性质,含30°的直角三角形
【分析】根据含30°的直角三角形可知∠BAE=∠DAF=30°,故可求出∠B=∠D=60°,∠BAD=120°,故可求出∠EAF的度数.
解:∵AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点
∴BE=AB,∠AEB=90°,
∴∠BAE=30°,
同理得∠DAF=30°,
根据菱形的性质可得∠B=∠D=60°,∠BAD=120°,
∴∠EAF=120°-30°-30°=60°.
【点睛】此题主要考查菱形内的角度计算,解题的关键是熟知含30°直角三角形的性质.
9.【考点】菱形的性质,直角三角形斜边的中线
【分析】由四边形ABCD是菱形,可知AC⊥BD,根据直角三角形斜边的中线等于斜边的一半可求出CD=10,根据勾股定理求出OC的长,然后由菱形的面积等于对角线乘积的一半即可求解.
解:∵四边形ABCD是菱形,
∴AC⊥BD,,,
∴CD=2OE=10,
∴,
∴AC=2OC=16,
∴菱形的面积为:.
故选A.
【点睛】本题考查了菱形的性质,直角三角形斜边的中线等于斜边的一半,勾股定理等知识,熟练掌握菱形的性质是解答本题的关键. 菱形的性质有:具有平行四边形的性质;菱形的四条边相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有两条对称轴.
10.【考点】正方形的性质,等边三角形的性质
【分析】根据等边三角形的性质及正方形的性质可得到AB=AE,从而可求得∠BAE的度数,则∠AEB的度数就不难求了.
解:根据等边三角形和正方形的性质可知AB=AE, ∴∠BAE=90°+60°=150°, ∴∠AEB=(180°-150°)÷2=15°. 故选:B.
【点睛】本题考查正方形和等边三角形的特殊性质,解题关键是熟练掌握性质.
11.【考点】菱形的性质,勾股定理
【分析】首先利用菱形的性质结合勾股定理得出BC的长,再利用三角形面积求出答案.
解:∵四边形ABCD是菱形,AC=6cm,BD=8cm,
∴AO=CO=3cm,BO=DO=4cm,∠BOC=90°,
∴BC==5(cm),
∴AE×BC=BO×AC
故5AE=24,
解得:AE=.
故选C.
【点睛】此题主要考查了菱形的性质以及勾股定理,正确利用三角形面积求出AE的长是解题关键.
12.【考点】正方形的性质,全等三角形的判定与性质
【分析】如图,根据正方形的性质得OD=OC,∠ODA=∠OCD=45°,∠DOC=90°,再利用等角的余角相等得到∠DOE=∠COF,于是可根据“ASA”证明△ODE≌△OCF,
则S△ODE=S△OCF,所以S四边形EOFD=S△DOC=S正方形ABCD.
解:如图,
∵四边形ABCD为正方形,
∴OD=OC,∠ODA=∠OCD=45°,∠DOC=90°,
而∠POM=90°,
即∠DOF+∠COF=90°,∠DOE+∠DOF=90°,
∴∠DOE=∠COF,
在△ODE和△OCF中,
,
∴△ODE≌△OCF(ASA),
∴S△ODE=S△OCF,
∴S四边形EOFD=S△DOC=S正方形ABCD=×42=4(cm2).
故选:D.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键,也是本题的难点.
13.【考点】正方形的性质,菱形的性质,等边三角形的判定和性质
【分析】由菱形的性质可得AB=BC,且∠B=60°,可得AC=AB=3,由正方形的性质可得AC=EF=3.
解:∵四边形ABCD是菱形 ∴AB=BC,且∠B=60°, ∴△ABC是等边三角形, ∴AB=AC=3, ∵四边形ACEF是正方形, ∴AC=EF=3 故答案为:3
【点睛】本题考查了正方形的性质,菱形的性质,等边三角形的判定和性质,熟练运用这些性质解决问题是本题的关键.
14.【考点】菱形的性质,勾股定理
【分析】画出图形,设菱形的边长为x,根据勾股定理求出周长即可.
解:当两张纸条如图所示放置时,菱形周长最大,设这时菱形的边长为xcm, 在Rt△ABC中, 由勾股定理:x2=(8-x)2+22, 解得:x=,
∴4x=17, 即菱形的最大周长为17cm. 故答案是:17.
【点睛】解答关键是怎样放置纸条使得到的菱形的周长最大,然后根据图形列方程.
15.【考点】矩形的性质,含30°角的直角三角形
【分析】由矩形的性质得出∠BAD=90°,由直角三角形30度角的性质和勾股定理计算AD的长,根据矩形的面积公式可得结论.
解:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AB=4,∠ADB=30°,
∴BD=8,
∴AD==4,
∴S矩形ABCD=AB?AD=4×4=16,
故答案为:16.
【点睛】此题考查了矩形的性质、含30°角的直角三角形的性质.熟练掌握直角三角形30度角的性质是关键.
16.【考点】翻折变换(折叠问题),矩形的性质,勾股定理
【分析】过作于,根据矩形的性质得到,推出四边形是矩形,得到,,根据折叠的性质得到,设,则,根据勾股定理列方程即可得到结论.
解:过作于,
四边形是矩形,
,
四边形是矩形,
,,
将纸片折叠,使点与点重合,折痕交于点,
,
设,则,
,
在中,,
,
解得:,
故答案为:.
【点睛】本题考查了翻折变换(折叠问题),矩形的性质,勾股定理,正确的作出辅助线是解题的关键.
17.【考点】等边三角形的性质,正方形的性质
【分析】根据已知可求得∠BEC的度数,根据三角形外角定理可求得∠AGD的度数.
解:∵四边形ABCD是正方形,
∴AB=BC=AD=CD,∠ABC=90°,∠ADG=∠CDG,∠ABD=45°,
∵GD=GD,
∴△ADG≌△CDG,
∴∠AGD=∠CGD,
∵∠CGD=∠EGB,
∴∠AGD=∠EGB,
∵△ABE是等边三角形,
∴AB=BE,∠ABE=60°,
∴BE=BC,∠EBC=150°,
∴∠BEC=∠ECB=15°,
∴∠BGE=180°﹣∠BEC﹣∠EBG=180°﹣15°﹣60°﹣45°=60°,
∴∠AGD=60°
故答案为60.
【点睛】本题考查等边三角形的性质及正方形的性质的运用.
18.【考点】轴对称-最短问题,菱形的性质
【分析】如图,连接OD,BD,作DH⊥AB于H,EG⊥AB于G.由四边形ADEF是菱形,推出F,D关于直线AE对称,推出PF=PD,推出PF+PB=PA+PB,由PD+PB≥BD,推出PF+PB的最小值是线段BD的长.
解:如图,连接OD,BD,作DH⊥AB于H,EG⊥AB于G.
∵四边形ADEF是菱形,
∴F,D关于直线AE对称,
∴PF=PD,
∴PF+PB=PA+PB,
∵PD+PB≥BD,
∴PF+PB的最小值是线段BD的长,
∵∠CAB=180°-105°-45°=30°,设AF=EF=AD=x,则DH=EG=x,FG=x,
∵∠EGB=45°,EG⊥BG,
∴EG=BG=x,
∴x+x+x=3+,
∴x=2,
∴DH=1,BH=3,
∴BD==,
∴PF+PB的最小值为,
故答案为:.
【点睛】本题考查轴对称-最短问题,菱形的性质等知识,解题的关键是学会用转化的思想思考问题,学会利用轴对称解决最短问题.
19.【考点】矩形的性质,菱形判定
【分析】直接利用平行四边形的判定方法得出四边形OCED是平行四边形,再利用矩形的性质以及菱形的判定方法得出答案.
证明:∵DE∥AC,CE∥BD, ∴四边形OCED是平行四边形, ∵四边形ABCD是矩形, ∴AO=OC=OB=OD=AC=BD, ∴四边形OCED是菱形.
【点睛】此题主要考查了矩形的性质以及菱形判定方法,正确掌握相关四边形判定与性质是解题关键.
20.【考点】正方形性质,勾股定理及逆定理
【分析】根据勾股定理求出BE2、EF2、BF2,根据勾股定理的逆定理判断即可.
解:∵△BEF是直角三角形,
理由是:∵在正方形ABCD中,AB=4,AE=2,DF=1,
∴∠A=∠C=∠D=90°,AB=AD=DC=BC=4,DE=4﹣2=2,CF=4﹣1=3,
∵由勾股定理得:BE2=AB2+AE2=42+22=20,EF2=DE2+DF2=22+12=5,BF2=BC2+CF2=42+32=25,
∴BE2+EF2=BF2,
∴∠BEF=90°,
即△BEF是直角三角形.
【点睛】本题考查了正方形性质,勾股定理,勾股定理的逆定理的应用,解此题的关键是求出BE2+EF2=BF2,注意:一个三角形的两边a、b的平方和等于第三边c的平方,那么这个三角形是直角三角形,难度适中.
21.【考点】平行线的性质,矩形的性质,翻折变换
【分析】直接利用翻折变换的性质,结合矩形的性质得出∠CBN=∠2=∠3,进而得出∠BOC=90°,求出答案即可.
解:∵将长方形纸片ABCD沿AC翻折,点B落在点E处,
∴∠2=∠3,∠ABC=∠E=90°.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠1=∠CBN.
∵∠1=∠3,
∴∠1=∠CBN=∠2=∠3.
∵AE∥BD,
∴∠BOC=∠E=90°,
∴∠CBN+∠2+∠3=90°,
∴∠CBN=∠2=∠3=30°,
∴∠EAC=90°﹣∠2=60°.
【点睛】本题考查了平行线的性质以及矩形的性质和翻折变换,根据题意得出∠CBN=∠2=∠3是解题的关键.
22.【考点】矩形的性质,全等三角形的判定和性质
【分析】(1)根据矩形的性质解答即可;
(2)根据全等三角形的判定和性质以及等腰直角三角形的性质解答即可.
证明:(1)∵四边形ABCD为矩形,
∴AD=BC,∠BAD=∠ADC=90°,
∵AF平分∠BAD,
∴∠DAF=45°,
∴AD=DF,
∴BC=DF;
(2)连接CG,BG,
∵点G为EF的中点,
∴GF=CG,
∴∠F=∠BCG=45°,
在△BCG与△DFG中,
∴△BCG≌△DFG(SAS),
∴BG=DG,∠CBG=∠FDG,
∴△BDG为等腰直角三角形,
∴BD=DG,
∴BD:DG=:1.
【点睛】此题考查矩形的性质,关键是根据矩形的性质和全等三角形的判定和性质解答.
23.【考点】全等三角形的判定与性质,平行四边形的判定,菱形的判定
【分析】(1)证明RtΔDFC?RtΔDEC(HL),根据全等三角形的性质即可得证;
(2)先证明ΔDEC≌ΔBEC(SAS),继而证明四边形ABCD为平行四边形,再根据BC=CD,即可得证.
解:(1)∵CE⊥BD,
∴∠DEC=90°,
∴,
在和中,
,,
∴,
∴;
(2)∵,,
∴,
又∵,,
∴,
∴,,
又∵,∴,
∴,而,
∴四边形为平行四边形,而,
∴四边形ABCD为菱形.
【点睛】本题考查了全等三角形的判定与性质,平行四边形的判定,菱形的判定等,熟练掌握相关的性质定理与判定定理是解题的关键.
24.【考点】折叠问题,全等三角形的判定和性质,平行四边形的性质,菱形的判定
【分析】(1)由题意可得AD=BC=B'C,∠B=∠D=∠B',且∠AED=∠CEB',利用AAS证明全等,则结论可得; (2)由△AED≌△CEB′可得AE=CE,且EF⊥AC,根据等腰三角形的性质可得EF垂直平分AC,∠AEF=∠CEF.即AF=CF,∠CEF=∠AFE=∠AEF,可得AE=AF,则可证四边形AECF是菱形.
证明:(1)∵四边形ABCD是平行四边形
∴AD=BC,CD∥AB,∠B=∠D
∵平行四边形ABCD沿其对角线AC折叠
∴BC=B'C,∠B=∠B'
∴∠D=∠B',AD=B'C且∠DEA=∠B'EC
∴△ADE≌△B'EC
(2)四边形AECF是菱形
∵△ADE≌△B'EC
∴AE=CE
∵AE=CE,EF⊥AC
∴EF垂直平分AC,∠AEF=∠CEF
∴AF=CF
∵CD∥AB
∴∠CEF=∠EFA且∠AEF=∠CEF
∴∠AEF=∠EFA
∴AF=AE
∴AF=AE=CE=CF
∴四边形AECF是菱形
【点睛】本题考查了折叠问题,全等三角形的判定和性质,平行四边形的性质,菱形的判定,熟练掌握这些性质和判定是解决问题的关键.
25.【考点】矩形的性质判定,等腰三角形的性质和判定,勾股定理
【分析】(1)根据CF平分∠ACD,且MN∥BD可证OF=OC,同理可证OE=OC,即可得OE=OF; (2)根据三角形的内角和定理和等腰三角形的性质可求∠ECF=90°,根据勾股定理可求EF的长,根据直角三角形斜边上中线等于斜边的一半,可得OC的长; (3)当点O在AC的中点时,由(1)知OE=OF,可证四边形AECF是平行四边形,再根据∠ECF=90°,可证四边形AECF是矩形.
解:(1)OE=OF,理由如下:
∵CF平分∠ACD,且MN∥BD ∴∠ACF=∠FCD=∠CFO ∴OF=OC 同理可证:OC=OE ∴OE=OF (2)由(1)知:OF=OC=OE ∴∠OCF=∠OFC,∠OCE=∠OEC ∴∠OCF+∠OCE=∠OFC+∠OEC 而∠OCF+∠OCE+∠OFC+∠OEC=180° ∴∠ECF=∠OCF+∠OCE=90° ∴EF===10
∴OC=EF=5 (3)当点O移动到AC中点时,四边形AECF为矩形 理由如下: ∵当点O移动到AC中点时 ∴OA=OC且OE=OF ∴四边形AECF为平行四边形 又∵∠ECF=90° ∴四边形AECF为矩形
【点睛】本题考查了矩形的性质判定,等腰三角形的性质和判定,勾股定理,熟练运用这些性质解决问题是本题的关键.
26.【考点】正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线,勾股定理
【分析】(1)①如图1①,要证BF=AE,只需证△ABE≌△BCF,只需证到∠BAE=∠CBF即可;
②延长AD,交射线BM于点G,如图1②,由△ABE≌△BCF可得BE=CF,由此可得CF=DF,从而可证到△DGF≌△CBF,则有DG=BC,从而可得DG=AD,然后运用直角三角形斜边上的中线等于斜边的一半即可解决问题;
(2)可分点F在CD上和点F在AD上两种情况进行讨论.当点F在CD上时,如图2①,易证Rt△ABE≌Rt△BCF(HL),则有∠BAE=∠CBF,由此可证到∠AOB=90°,然后在Rt△ABE中,运用面积法就可求出BO的长;当点F在AD上时,如图2②,易证Rt△ABE≌Rt△BAF(HL),则有∠BAE=∠ABF,根据等角对等边可得OB=OA,根据等角的余角相等可得∠AEB=∠EBF,根据等角对等边可得OB=OE,即可得到OA=OB=OE,只需求出AE的长就可解决问题.
解:(1)①如图1①,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABE=∠C=90°,
∴∠BAE+∠AEB=90°,
∵BF⊥AE,
∴∠CBF+∠AEB=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(ASA),
∴BF=AE;
②OD=AB.
证明:延长AD,交射线BM于点G,如图1②,
∵△ABE≌△BCF,
∴BE=CF.
∵E为BC的中点,
∴CF=BE=BC=DC,
∴CF=DF.
∵DG∥BC,
∴∠DGF=∠CBF.
在△DGF和△CBF中,
,
∴△DGF≌△CBF,
∴DG=BC,
∴DG=AD.
∵BF⊥AE,
∴OD=AG=AD=AB;
(2)①若点F在CD上,如图2①,
在Rt△ABE和Rt△BCF中,
,
∴Rt△ABE≌Rt△BCF(HL),
∴∠BAE=∠CBF,
∵∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴∠AOB=90°.
∵∠ABE=90°,AB=4,BE=2,
∴AE==2 .
∵S△ABE=AB?BE=AE?BO,
∴BO=.
②若点F在AD上,如图2②,
在Rt△ABE和Rt△BAF中,
,
∴Rt△ABE≌Rt△BAF(HL),
∴∠BAE=∠ABF,
∴OB=OA.
∵∠BAE+∠AEB=90°,∠ABF+∠EBF=90°,
∴∠AEB=∠EBF,
∴OB=OE,
∴OA=OB=OE.
∵∠ABE=90°,AB=4,BE=2,
∴AE==2,
∴OB=AE=.
综上所述:BO的长为或.
【点睛】本题考查了正方形的性质、全等三角形的判定与性质、直角三角形斜边上的中线等于斜边的一半、等角对等边、等角的余角相等、勾股定理等知识,运用直角三角形斜边上的中线等于斜边的一半是解决第(1)②小题的关键,运用分类讨论是解决第(2)小题的关键.
班级_____________考号______________姓名_______________总分_________________
一、选择题(12小题,每题3分,共36分)
1.如图,在菱形ABCD中,∠A=130°,连接BD,∠DBC等于( )
A.25° B.35° C.50° D.65°
2.四边形的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AC=BD C.AB=BC D.AD=BC
3.如图,在长方形ABCD中,已知,,将AD沿直线AF折叠,使点D落在BC的点E处,则CF的长是
A.1cm B.2cm C.3cm D.4cm
4.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AO=4,则AB的长是( )
A.4 B.5 C.6 D.8
5.如图,在矩形中,,点,,,分别是边,,,的中点,连接,,则图中矩形的个数共有( )
A.5个 B.8个 C.9个 D.11个
6.如图,是菱形的对角线,分别是边的中点,连接,,则下列结论错误的是( )
A. B. C.四边形是菱形 D.四边形是菱形
7.如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,若正方形ABCD周长为a,则EF+EG等于( )
A. B. C.a D.2a
8.在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点(如图),则∠EAF等于( ).
A.60° B.75° C.120° D.45°
9.如图,菱形ABCD对角线AC与BD交于点O,点E是DC边上的中点,连接OE.OE=5,BD=12,则菱形的面积为( )
A.96 B.48 C.192 D.24
10.如图,在正方形ABCD中,作等边三角形ADE,则∠AEB的度数为()
A.10° B.15° C.12.5° D.20°
11.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,过点A作AE垂直BC与点E,则AE的长是( )
A. B. C. D.
12.如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )
A.无法确定 B.8cm2 C.16cm2 D.4cm2
二、填空题(6小题,每题3分,共18分)
13.如图,菱形ABCD中,∠B=60°,AB=3,四边形ACEF是正方形,则EF的长为_____.
14.如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是_________.
15.如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则矩形ABCD的面积为_______.
16.如图,在矩形纸片中,,,边上有一点,,将纸片折叠,使点与点重合,折痕交于点,则线段的长是__.
17.如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是_____度.
18.如图,在△ABC中,AB=3+,∠B=45°,∠C=105°,点 D、E、F分别在AC、BC、AB上,且四边形ADEF为菱形,若点P是AE上一个动点,则PF+PB的最小值为___________ 。
三、解答题(8小题,共66分)
19.矩形ABCD的对角线AC、BD相交与O,DE//AC,CE//BD.求证:四边形OCED是菱形.
20.如图,在正方形ABCD中,AB=4,AE=2,DF=1,请你判定△BEF的形状,并说明理由.
21.如图,将长方形纸片ABCD沿AC翻折,点B落在点E处,连接BD,若∠1=∠3,AE∥BD,求∠EAC的度数.
22.如图,在矩形ABCD中,AF平分∠BAD交BC于E,交DC延长线于F,点G为EF的中点,连结DG.
(1)求证:BC=DF;
(2)连BD,求BD:DG的值.
23.如图,四边形中,,,于交的延长线于,,.
(1)求证:.
(2)求证:四边形是菱形.
24.如图,现将平行四边形ABCD沿其对角线AC折叠,使点B落在点B′处.AB′与CD交于点E.
(1)求证:△AED≌△CEB′;
(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.
25.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)若CE=8,CF=6,求OC的长
(3)连结AE,AF,当点O运动到何处时,四边形AECF是矩形?并说出你的理由.
26.已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
(1)若BF⊥AE,
①求证:BF=AE;
②连接OD,确定OD与AB的数量关系,并证明;
(2)若正方形的边长为4,且BF=AE,求BO的长.
参考答案
1.【考点】菱形的性质,等腰三角形的性质
【分析】直接利用菱形的性质得出∠C的度数,再利用等腰三角形的性质得出答案.
解:∵在菱形ABCD中,∠A=130°,
∴∠C=130°,BC=DC,
∴∠DBC=∠CDB=(180°-130°)=25°.
故选:A.
【点睛】此题主要考查了菱形的性质以及等腰三角形的性质,正确应用菱形的性质是解题关键.
2.【考点】矩形的判定
【分析】四边形ABCD的对角线互相平分,则说明四边形是平行四边形,由矩形的判定定理可得,只需添加条件是对角线相等.
解:可添加AC=BD,理由如下: ∵四边形ABCD的对角线互相平分, ∴四边形ABCD是平行四边形, ∵AC=BD,根据矩形判定定理对角线相等的平行四边形是矩形, ∴四边形ABCD是矩形. 故选:B.
【点睛】考查了矩形的判定,关键是矩形的判定:①矩形的定义:有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形.
3.【考点】翻折变换,矩形的性质,勾股定理
【分析】由矩形的性质和折叠的性质可得,,由勾股定理可求BE的长,即可得CE的长,再由勾股定理可求CF的长.
解:四边形ABCD是矩形,
,,
折叠
,,
在中,,
,
在中,,
故选:C.
【点睛】本题考查了翻折变换,矩形的性质,勾股定理,熟练掌握折叠的性质是本题的关键.
4.【考点】矩形的性质,等边三角形的性质和判定
【分析】根据矩形性质得出AO=OC,BO=OD,AC=BD,推出OA=OB,得出△AOB是等边三角形,推出AB=AO=4即可.
解:∵四边形ABCD是矩形,
∴AO=OC,BO=OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=4,
故选:A.
【点睛】本题考查了矩形的性质,等边三角形的性质和判定的应用;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.
5.【考点】矩形的判定
【分析】根据矩形的判定定理解答.
解:∵E,G分别是边DA,BC的中点,四边形ABCD是矩形,
∴四边形DEGC、AEGB是矩形,
同理四边形ADHF、BCHF是矩形,
则图中四个小四边形是矩形,
故图中矩形的个数共有9个,
故选:C.
【点睛】本题考查的是矩形的判定,掌握矩形的判定定理是解题的关键.
6.【考点】菱形的性质和判定,三角形的中位线定理,平行四边形的判定
【分析】根据菱形的性质和三角形的中位线以及菱形的判定可得AC⊥BD且DO=BD,再根据三角形的中位线可得EF=BD,即可得出结论
解:∵是菱形的对角线,
∴AC⊥BD且DO=BD,
∵分别是边的中点,
∴EF=BD,EF//BD,
∴EF=DO, ∴选项A正确.
∵AC⊥BD,EF//BD
∴,∴选项B正确.
∵是菱形的对角线,
∴BC=CD,O为AC的中点
∵分别是边的中点,
∴EO//BC//AD,FO//CD//AB且EO=FO=BC=DC
∴四边形是菱形∴选项C正确.
∵EF//BD,FO//AB
∴.四边形是平行四边形
∴选项D错误.
故选:D.
【点睛】本题考查了菱形的性质和判定、三角形的中位线定理、平行四边形的判定以及平行线的性质,熟练掌握相关知识是解题的关键.
7.【考点】正方形的性质,矩形的性质和判定
【分析】由正方形的性质可知∠BAC=∠ACB,又知EF⊥AB,EG⊥BC,可得EG=CG,EF=GB,从而求出EF+EG=BC即可.
解:∵E是正方形ABCD对角线AC上一点,
∴∠BAC=∠ACB=45°,∠B=90°
∵EF⊥AB,EG⊥BC,F、G是垂足,
∴四边形EFBG是矩形,三角形CGE是等腰直角三角形
∴EG=CG,EF=BG,
∴EF+EG=BC
∵正方形ABCD周长为a,
∴BC=,
∴EF+EG=,
故选:A.
【点睛】本题主要考查正方形的性质、矩形的性质和判定,利用等腰直角三角形的性质解决所求问题.
8.【考点】菱形的性质,含30°的直角三角形
【分析】根据含30°的直角三角形可知∠BAE=∠DAF=30°,故可求出∠B=∠D=60°,∠BAD=120°,故可求出∠EAF的度数.
解:∵AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点
∴BE=AB,∠AEB=90°,
∴∠BAE=30°,
同理得∠DAF=30°,
根据菱形的性质可得∠B=∠D=60°,∠BAD=120°,
∴∠EAF=120°-30°-30°=60°.
【点睛】此题主要考查菱形内的角度计算,解题的关键是熟知含30°直角三角形的性质.
9.【考点】菱形的性质,直角三角形斜边的中线
【分析】由四边形ABCD是菱形,可知AC⊥BD,根据直角三角形斜边的中线等于斜边的一半可求出CD=10,根据勾股定理求出OC的长,然后由菱形的面积等于对角线乘积的一半即可求解.
解:∵四边形ABCD是菱形,
∴AC⊥BD,,,
∴CD=2OE=10,
∴,
∴AC=2OC=16,
∴菱形的面积为:.
故选A.
【点睛】本题考查了菱形的性质,直角三角形斜边的中线等于斜边的一半,勾股定理等知识,熟练掌握菱形的性质是解答本题的关键. 菱形的性质有:具有平行四边形的性质;菱形的四条边相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有两条对称轴.
10.【考点】正方形的性质,等边三角形的性质
【分析】根据等边三角形的性质及正方形的性质可得到AB=AE,从而可求得∠BAE的度数,则∠AEB的度数就不难求了.
解:根据等边三角形和正方形的性质可知AB=AE, ∴∠BAE=90°+60°=150°, ∴∠AEB=(180°-150°)÷2=15°. 故选:B.
【点睛】本题考查正方形和等边三角形的特殊性质,解题关键是熟练掌握性质.
11.【考点】菱形的性质,勾股定理
【分析】首先利用菱形的性质结合勾股定理得出BC的长,再利用三角形面积求出答案.
解:∵四边形ABCD是菱形,AC=6cm,BD=8cm,
∴AO=CO=3cm,BO=DO=4cm,∠BOC=90°,
∴BC==5(cm),
∴AE×BC=BO×AC
故5AE=24,
解得:AE=.
故选C.
【点睛】此题主要考查了菱形的性质以及勾股定理,正确利用三角形面积求出AE的长是解题关键.
12.【考点】正方形的性质,全等三角形的判定与性质
【分析】如图,根据正方形的性质得OD=OC,∠ODA=∠OCD=45°,∠DOC=90°,再利用等角的余角相等得到∠DOE=∠COF,于是可根据“ASA”证明△ODE≌△OCF,
则S△ODE=S△OCF,所以S四边形EOFD=S△DOC=S正方形ABCD.
解:如图,
∵四边形ABCD为正方形,
∴OD=OC,∠ODA=∠OCD=45°,∠DOC=90°,
而∠POM=90°,
即∠DOF+∠COF=90°,∠DOE+∠DOF=90°,
∴∠DOE=∠COF,
在△ODE和△OCF中,
,
∴△ODE≌△OCF(ASA),
∴S△ODE=S△OCF,
∴S四边形EOFD=S△DOC=S正方形ABCD=×42=4(cm2).
故选:D.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键,也是本题的难点.
13.【考点】正方形的性质,菱形的性质,等边三角形的判定和性质
【分析】由菱形的性质可得AB=BC,且∠B=60°,可得AC=AB=3,由正方形的性质可得AC=EF=3.
解:∵四边形ABCD是菱形 ∴AB=BC,且∠B=60°, ∴△ABC是等边三角形, ∴AB=AC=3, ∵四边形ACEF是正方形, ∴AC=EF=3 故答案为:3
【点睛】本题考查了正方形的性质,菱形的性质,等边三角形的判定和性质,熟练运用这些性质解决问题是本题的关键.
14.【考点】菱形的性质,勾股定理
【分析】画出图形,设菱形的边长为x,根据勾股定理求出周长即可.
解:当两张纸条如图所示放置时,菱形周长最大,设这时菱形的边长为xcm, 在Rt△ABC中, 由勾股定理:x2=(8-x)2+22, 解得:x=,
∴4x=17, 即菱形的最大周长为17cm. 故答案是:17.
【点睛】解答关键是怎样放置纸条使得到的菱形的周长最大,然后根据图形列方程.
15.【考点】矩形的性质,含30°角的直角三角形
【分析】由矩形的性质得出∠BAD=90°,由直角三角形30度角的性质和勾股定理计算AD的长,根据矩形的面积公式可得结论.
解:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AB=4,∠ADB=30°,
∴BD=8,
∴AD==4,
∴S矩形ABCD=AB?AD=4×4=16,
故答案为:16.
【点睛】此题考查了矩形的性质、含30°角的直角三角形的性质.熟练掌握直角三角形30度角的性质是关键.
16.【考点】翻折变换(折叠问题),矩形的性质,勾股定理
【分析】过作于,根据矩形的性质得到,推出四边形是矩形,得到,,根据折叠的性质得到,设,则,根据勾股定理列方程即可得到结论.
解:过作于,
四边形是矩形,
,
四边形是矩形,
,,
将纸片折叠,使点与点重合,折痕交于点,
,
设,则,
,
在中,,
,
解得:,
故答案为:.
【点睛】本题考查了翻折变换(折叠问题),矩形的性质,勾股定理,正确的作出辅助线是解题的关键.
17.【考点】等边三角形的性质,正方形的性质
【分析】根据已知可求得∠BEC的度数,根据三角形外角定理可求得∠AGD的度数.
解:∵四边形ABCD是正方形,
∴AB=BC=AD=CD,∠ABC=90°,∠ADG=∠CDG,∠ABD=45°,
∵GD=GD,
∴△ADG≌△CDG,
∴∠AGD=∠CGD,
∵∠CGD=∠EGB,
∴∠AGD=∠EGB,
∵△ABE是等边三角形,
∴AB=BE,∠ABE=60°,
∴BE=BC,∠EBC=150°,
∴∠BEC=∠ECB=15°,
∴∠BGE=180°﹣∠BEC﹣∠EBG=180°﹣15°﹣60°﹣45°=60°,
∴∠AGD=60°
故答案为60.
【点睛】本题考查等边三角形的性质及正方形的性质的运用.
18.【考点】轴对称-最短问题,菱形的性质
【分析】如图,连接OD,BD,作DH⊥AB于H,EG⊥AB于G.由四边形ADEF是菱形,推出F,D关于直线AE对称,推出PF=PD,推出PF+PB=PA+PB,由PD+PB≥BD,推出PF+PB的最小值是线段BD的长.
解:如图,连接OD,BD,作DH⊥AB于H,EG⊥AB于G.
∵四边形ADEF是菱形,
∴F,D关于直线AE对称,
∴PF=PD,
∴PF+PB=PA+PB,
∵PD+PB≥BD,
∴PF+PB的最小值是线段BD的长,
∵∠CAB=180°-105°-45°=30°,设AF=EF=AD=x,则DH=EG=x,FG=x,
∵∠EGB=45°,EG⊥BG,
∴EG=BG=x,
∴x+x+x=3+,
∴x=2,
∴DH=1,BH=3,
∴BD==,
∴PF+PB的最小值为,
故答案为:.
【点睛】本题考查轴对称-最短问题,菱形的性质等知识,解题的关键是学会用转化的思想思考问题,学会利用轴对称解决最短问题.
19.【考点】矩形的性质,菱形判定
【分析】直接利用平行四边形的判定方法得出四边形OCED是平行四边形,再利用矩形的性质以及菱形的判定方法得出答案.
证明:∵DE∥AC,CE∥BD, ∴四边形OCED是平行四边形, ∵四边形ABCD是矩形, ∴AO=OC=OB=OD=AC=BD, ∴四边形OCED是菱形.
【点睛】此题主要考查了矩形的性质以及菱形判定方法,正确掌握相关四边形判定与性质是解题关键.
20.【考点】正方形性质,勾股定理及逆定理
【分析】根据勾股定理求出BE2、EF2、BF2,根据勾股定理的逆定理判断即可.
解:∵△BEF是直角三角形,
理由是:∵在正方形ABCD中,AB=4,AE=2,DF=1,
∴∠A=∠C=∠D=90°,AB=AD=DC=BC=4,DE=4﹣2=2,CF=4﹣1=3,
∵由勾股定理得:BE2=AB2+AE2=42+22=20,EF2=DE2+DF2=22+12=5,BF2=BC2+CF2=42+32=25,
∴BE2+EF2=BF2,
∴∠BEF=90°,
即△BEF是直角三角形.
【点睛】本题考查了正方形性质,勾股定理,勾股定理的逆定理的应用,解此题的关键是求出BE2+EF2=BF2,注意:一个三角形的两边a、b的平方和等于第三边c的平方,那么这个三角形是直角三角形,难度适中.
21.【考点】平行线的性质,矩形的性质,翻折变换
【分析】直接利用翻折变换的性质,结合矩形的性质得出∠CBN=∠2=∠3,进而得出∠BOC=90°,求出答案即可.
解:∵将长方形纸片ABCD沿AC翻折,点B落在点E处,
∴∠2=∠3,∠ABC=∠E=90°.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠1=∠CBN.
∵∠1=∠3,
∴∠1=∠CBN=∠2=∠3.
∵AE∥BD,
∴∠BOC=∠E=90°,
∴∠CBN+∠2+∠3=90°,
∴∠CBN=∠2=∠3=30°,
∴∠EAC=90°﹣∠2=60°.
【点睛】本题考查了平行线的性质以及矩形的性质和翻折变换,根据题意得出∠CBN=∠2=∠3是解题的关键.
22.【考点】矩形的性质,全等三角形的判定和性质
【分析】(1)根据矩形的性质解答即可;
(2)根据全等三角形的判定和性质以及等腰直角三角形的性质解答即可.
证明:(1)∵四边形ABCD为矩形,
∴AD=BC,∠BAD=∠ADC=90°,
∵AF平分∠BAD,
∴∠DAF=45°,
∴AD=DF,
∴BC=DF;
(2)连接CG,BG,
∵点G为EF的中点,
∴GF=CG,
∴∠F=∠BCG=45°,
在△BCG与△DFG中,
∴△BCG≌△DFG(SAS),
∴BG=DG,∠CBG=∠FDG,
∴△BDG为等腰直角三角形,
∴BD=DG,
∴BD:DG=:1.
【点睛】此题考查矩形的性质,关键是根据矩形的性质和全等三角形的判定和性质解答.
23.【考点】全等三角形的判定与性质,平行四边形的判定,菱形的判定
【分析】(1)证明RtΔDFC?RtΔDEC(HL),根据全等三角形的性质即可得证;
(2)先证明ΔDEC≌ΔBEC(SAS),继而证明四边形ABCD为平行四边形,再根据BC=CD,即可得证.
解:(1)∵CE⊥BD,
∴∠DEC=90°,
∴,
在和中,
,,
∴,
∴;
(2)∵,,
∴,
又∵,,
∴,
∴,,
又∵,∴,
∴,而,
∴四边形为平行四边形,而,
∴四边形ABCD为菱形.
【点睛】本题考查了全等三角形的判定与性质,平行四边形的判定,菱形的判定等,熟练掌握相关的性质定理与判定定理是解题的关键.
24.【考点】折叠问题,全等三角形的判定和性质,平行四边形的性质,菱形的判定
【分析】(1)由题意可得AD=BC=B'C,∠B=∠D=∠B',且∠AED=∠CEB',利用AAS证明全等,则结论可得; (2)由△AED≌△CEB′可得AE=CE,且EF⊥AC,根据等腰三角形的性质可得EF垂直平分AC,∠AEF=∠CEF.即AF=CF,∠CEF=∠AFE=∠AEF,可得AE=AF,则可证四边形AECF是菱形.
证明:(1)∵四边形ABCD是平行四边形
∴AD=BC,CD∥AB,∠B=∠D
∵平行四边形ABCD沿其对角线AC折叠
∴BC=B'C,∠B=∠B'
∴∠D=∠B',AD=B'C且∠DEA=∠B'EC
∴△ADE≌△B'EC
(2)四边形AECF是菱形
∵△ADE≌△B'EC
∴AE=CE
∵AE=CE,EF⊥AC
∴EF垂直平分AC,∠AEF=∠CEF
∴AF=CF
∵CD∥AB
∴∠CEF=∠EFA且∠AEF=∠CEF
∴∠AEF=∠EFA
∴AF=AE
∴AF=AE=CE=CF
∴四边形AECF是菱形
【点睛】本题考查了折叠问题,全等三角形的判定和性质,平行四边形的性质,菱形的判定,熟练掌握这些性质和判定是解决问题的关键.
25.【考点】矩形的性质判定,等腰三角形的性质和判定,勾股定理
【分析】(1)根据CF平分∠ACD,且MN∥BD可证OF=OC,同理可证OE=OC,即可得OE=OF; (2)根据三角形的内角和定理和等腰三角形的性质可求∠ECF=90°,根据勾股定理可求EF的长,根据直角三角形斜边上中线等于斜边的一半,可得OC的长; (3)当点O在AC的中点时,由(1)知OE=OF,可证四边形AECF是平行四边形,再根据∠ECF=90°,可证四边形AECF是矩形.
解:(1)OE=OF,理由如下:
∵CF平分∠ACD,且MN∥BD ∴∠ACF=∠FCD=∠CFO ∴OF=OC 同理可证:OC=OE ∴OE=OF (2)由(1)知:OF=OC=OE ∴∠OCF=∠OFC,∠OCE=∠OEC ∴∠OCF+∠OCE=∠OFC+∠OEC 而∠OCF+∠OCE+∠OFC+∠OEC=180° ∴∠ECF=∠OCF+∠OCE=90° ∴EF===10
∴OC=EF=5 (3)当点O移动到AC中点时,四边形AECF为矩形 理由如下: ∵当点O移动到AC中点时 ∴OA=OC且OE=OF ∴四边形AECF为平行四边形 又∵∠ECF=90° ∴四边形AECF为矩形
【点睛】本题考查了矩形的性质判定,等腰三角形的性质和判定,勾股定理,熟练运用这些性质解决问题是本题的关键.
26.【考点】正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线,勾股定理
【分析】(1)①如图1①,要证BF=AE,只需证△ABE≌△BCF,只需证到∠BAE=∠CBF即可;
②延长AD,交射线BM于点G,如图1②,由△ABE≌△BCF可得BE=CF,由此可得CF=DF,从而可证到△DGF≌△CBF,则有DG=BC,从而可得DG=AD,然后运用直角三角形斜边上的中线等于斜边的一半即可解决问题;
(2)可分点F在CD上和点F在AD上两种情况进行讨论.当点F在CD上时,如图2①,易证Rt△ABE≌Rt△BCF(HL),则有∠BAE=∠CBF,由此可证到∠AOB=90°,然后在Rt△ABE中,运用面积法就可求出BO的长;当点F在AD上时,如图2②,易证Rt△ABE≌Rt△BAF(HL),则有∠BAE=∠ABF,根据等角对等边可得OB=OA,根据等角的余角相等可得∠AEB=∠EBF,根据等角对等边可得OB=OE,即可得到OA=OB=OE,只需求出AE的长就可解决问题.
解:(1)①如图1①,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABE=∠C=90°,
∴∠BAE+∠AEB=90°,
∵BF⊥AE,
∴∠CBF+∠AEB=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(ASA),
∴BF=AE;
②OD=AB.
证明:延长AD,交射线BM于点G,如图1②,
∵△ABE≌△BCF,
∴BE=CF.
∵E为BC的中点,
∴CF=BE=BC=DC,
∴CF=DF.
∵DG∥BC,
∴∠DGF=∠CBF.
在△DGF和△CBF中,
,
∴△DGF≌△CBF,
∴DG=BC,
∴DG=AD.
∵BF⊥AE,
∴OD=AG=AD=AB;
(2)①若点F在CD上,如图2①,
在Rt△ABE和Rt△BCF中,
,
∴Rt△ABE≌Rt△BCF(HL),
∴∠BAE=∠CBF,
∵∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴∠AOB=90°.
∵∠ABE=90°,AB=4,BE=2,
∴AE==2 .
∵S△ABE=AB?BE=AE?BO,
∴BO=.
②若点F在AD上,如图2②,
在Rt△ABE和Rt△BAF中,
,
∴Rt△ABE≌Rt△BAF(HL),
∴∠BAE=∠ABF,
∴OB=OA.
∵∠BAE+∠AEB=90°,∠ABF+∠EBF=90°,
∴∠AEB=∠EBF,
∴OB=OE,
∴OA=OB=OE.
∵∠ABE=90°,AB=4,BE=2,
∴AE==2,
∴OB=AE=.
综上所述:BO的长为或.
【点睛】本题考查了正方形的性质、全等三角形的判定与性质、直角三角形斜边上的中线等于斜边的一半、等角对等边、等角的余角相等、勾股定理等知识,运用直角三角形斜边上的中线等于斜边的一半是解决第(1)②小题的关键,运用分类讨论是解决第(2)小题的关键.
