沪科版数学八年级下册18.1勾股定理课件 共21张PPT
文档属性
| 名称 | 沪科版数学八年级下册18.1勾股定理课件 共21张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 313.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-22 12:13:00 | ||
图片预览



文档简介
课件21张PPT。 18.1 勾股定理
第一课时 1.观察图1-1(图中每个小方格代表一个单位面积)正方形A中含有 个小方格,即A的面积是
个单位面积.正方形B的面积是
个单位面积.正方形C的面积是
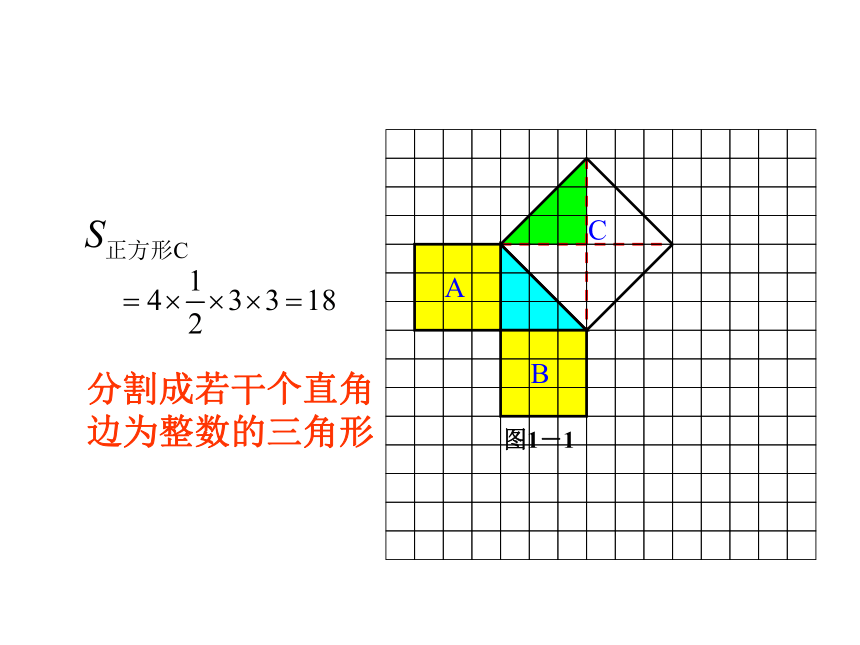
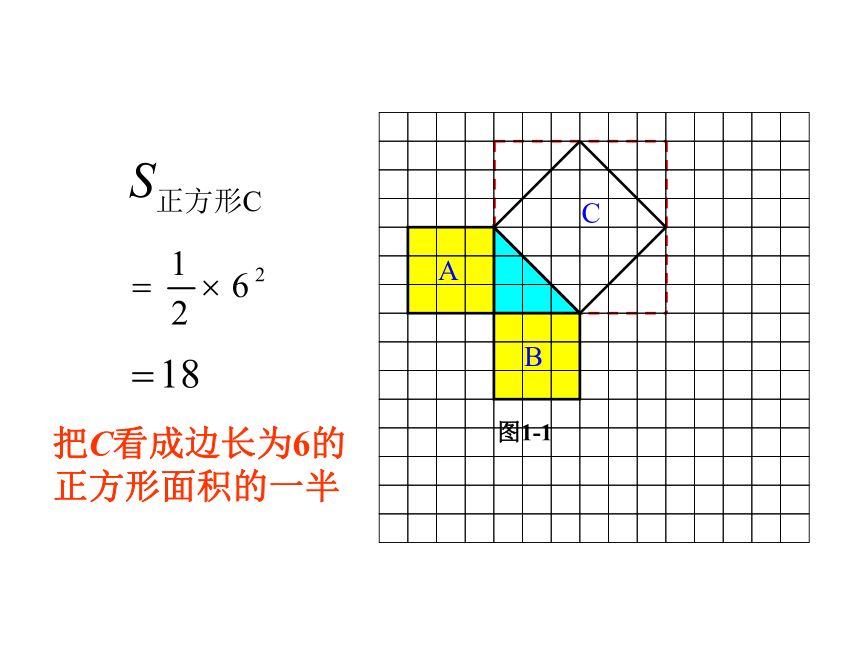
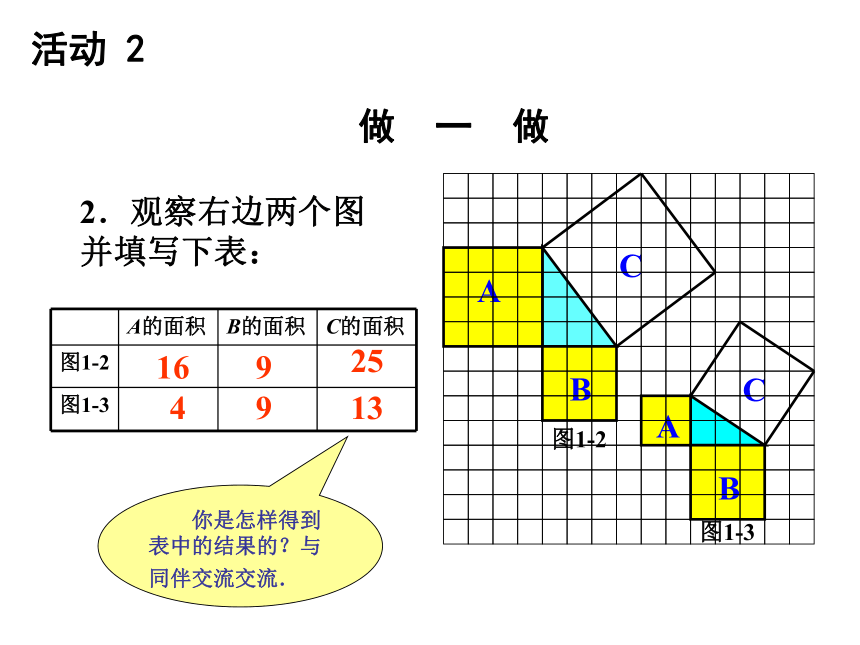
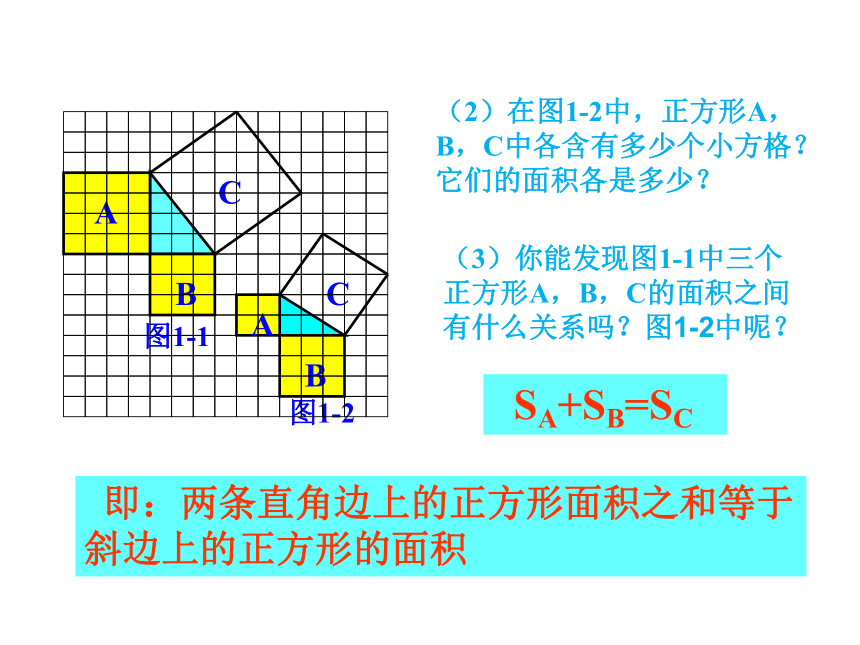
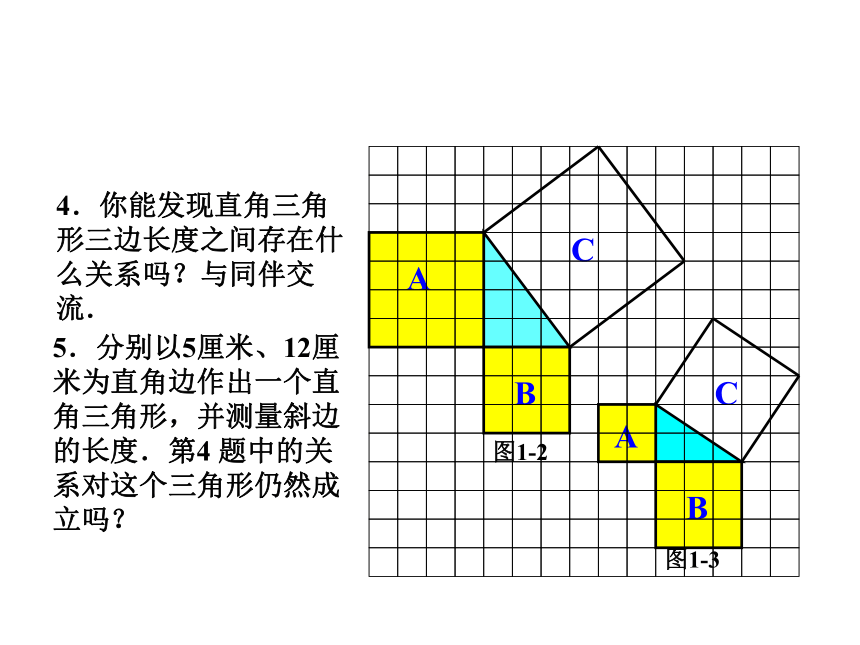
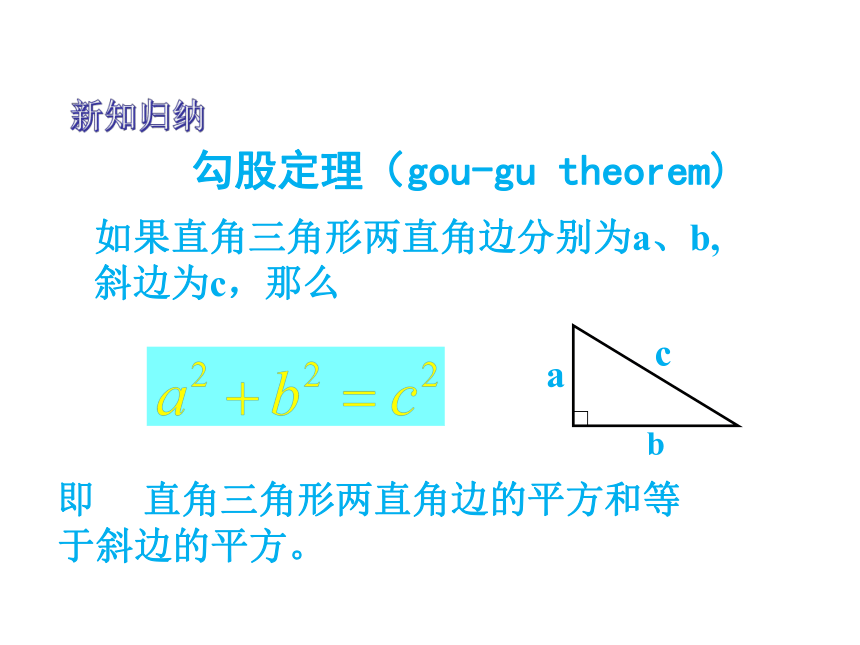
个单位面积.9918你是怎样得到上面的结果的?与同伴交流交流.9活动 1图1-1分割成若干个直角边为整数的三角形把C看成边长为6的正方形面积的一半2.观察右边两个图并填写下表:169254913 你是怎样得到表中的结果的?与同伴交流交流.做 一 做活动 2(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?图1-2中呢? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积4.你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流.5.分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度.第4 题中的关系对这个三角形仍然成立吗?新知归纳如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股定理(gou-gu theorem)在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.勾股世界 我国是最早了解勾股定理的国家之一。三千多年前,周朝数学家商高就提出了“勾三股四弦五”的说法。毕达哥拉斯 二千多年前,希腊的毕达哥拉斯学派证明了这个勾股定理,所以勾股定理又被称为“毕达哥拉斯定理”,不过毕达哥拉斯的发现比中国晚了500多年。勾股定理的证明 证法一利用4个形状大小相等的直角三角形,拼出以斜边c为边长的正方形,你能利用它能说明勾股定理吗?证法二:aabbcc伽菲尔德证法:∴ a2 + b2 = c21、求下列字母所代表的正方形的面积。解:正方形A的面积
=225+400 =625 解:正方形B的面积
=81+225 =306 随堂练习2、求出下列直角三角形中未知边的长度:解:由勾股定理得
x2 = 32+ 42=25.∵x>0,
∴x = 5.2、下列阴影部分是一个正方形,求此正方形的面积.解:设正方形的边长为x厘米 , 则 x2=172-152=64答:正方形的面积是64平方厘米.勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。方法总结c2=a2 + b2a2=c2-b2那你知道它们的变形吗?b2 =c2-a2例1 现在一楼房发生火灾,消防队员决定用消防车上的云梯救人。已知最多只能伸长10m,消防车高3m.救人是云梯伸至最长,在完成从9m高处救人后,还要从12m高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到0.1m)例题讲解分析:如图18-3,设A是云梯的下端点,AB是伸长后的云梯,B是第一次救人的地点,D是第二次救人的地点,过点A的水平线与楼房ED的交点为O。则OB=9-3=6(m),OD=12-3=9(m).根据勾股定理,得解方程,得设AC=X,则OC=8-x,于是根据勾股定理,得例2 已知:如图18-4,在Rt△ABC中,两直角边AC=5,
BC=12。求斜边上的高CD的长。解:在Rt△ABC中,又∵在Rt△ABC中,1这节课你学到了什么知识?3、你还有什么疑惑或没有弄懂的地方?2 运用“勾股定理”应注意什么问题?课堂小结
第一课时 1.观察图1-1(图中每个小方格代表一个单位面积)正方形A中含有 个小方格,即A的面积是
个单位面积.正方形B的面积是
个单位面积.正方形C的面积是
个单位面积.9918你是怎样得到上面的结果的?与同伴交流交流.9活动 1图1-1分割成若干个直角边为整数的三角形把C看成边长为6的正方形面积的一半2.观察右边两个图并填写下表:169254913 你是怎样得到表中的结果的?与同伴交流交流.做 一 做活动 2(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?图1-2中呢? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积4.你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流.5.分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度.第4 题中的关系对这个三角形仍然成立吗?新知归纳如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股定理(gou-gu theorem)在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.勾股世界 我国是最早了解勾股定理的国家之一。三千多年前,周朝数学家商高就提出了“勾三股四弦五”的说法。毕达哥拉斯 二千多年前,希腊的毕达哥拉斯学派证明了这个勾股定理,所以勾股定理又被称为“毕达哥拉斯定理”,不过毕达哥拉斯的发现比中国晚了500多年。勾股定理的证明 证法一利用4个形状大小相等的直角三角形,拼出以斜边c为边长的正方形,你能利用它能说明勾股定理吗?证法二:aabbcc伽菲尔德证法:∴ a2 + b2 = c21、求下列字母所代表的正方形的面积。解:正方形A的面积
=225+400 =625 解:正方形B的面积
=81+225 =306 随堂练习2、求出下列直角三角形中未知边的长度:解:由勾股定理得
x2 = 32+ 42=25.∵x>0,
∴x = 5.2、下列阴影部分是一个正方形,求此正方形的面积.解:设正方形的边长为x厘米 , 则 x2=172-152=64答:正方形的面积是64平方厘米.勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。方法总结c2=a2 + b2a2=c2-b2那你知道它们的变形吗?b2 =c2-a2例1 现在一楼房发生火灾,消防队员决定用消防车上的云梯救人。已知最多只能伸长10m,消防车高3m.救人是云梯伸至最长,在完成从9m高处救人后,还要从12m高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到0.1m)例题讲解分析:如图18-3,设A是云梯的下端点,AB是伸长后的云梯,B是第一次救人的地点,D是第二次救人的地点,过点A的水平线与楼房ED的交点为O。则OB=9-3=6(m),OD=12-3=9(m).根据勾股定理,得解方程,得设AC=X,则OC=8-x,于是根据勾股定理,得例2 已知:如图18-4,在Rt△ABC中,两直角边AC=5,
BC=12。求斜边上的高CD的长。解:在Rt△ABC中,又∵在Rt△ABC中,1这节课你学到了什么知识?3、你还有什么疑惑或没有弄懂的地方?2 运用“勾股定理”应注意什么问题?课堂小结
