2019年春华师大版九年级下册数学 课件:27.4 正多边形和圆 共19张PPT
文档属性
| 名称 | 2019年春华师大版九年级下册数学 课件:27.4 正多边形和圆 共19张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 785.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-13 13:59:35 | ||
图片预览





文档简介
课件19张PPT。27.4正多边形和圆目标引领1、知识与技能
1.了解正多边形的概念、正多边形与圆的关系.
2.会等分圆周,并会画出相应的正多边形.
3.会运用尺规作图画出特殊的正多边形
2、过程与方法
1.在探究正多边形与圆的关系中,培养学生动手能力和观察分析能力.
2.通过尺规作图以及分析书写作图步骤,提高学生分析问题和语言表达能力.
3、情感、态度与价值观
1.在学生动手画图的过程中体会数学的运用价值,提高学习兴趣.
2.在分组交流中学会合作与分享. 问题1,什么样的图形是正多边形?各边相等,各角也相等的多边形是正多边形.问题2,我们学习了正多边形的哪些性质?正多形是轴对称图形.新课导入预习导航1.任意画出正三角形、正四边形、正五边形和正六边形,然后画出它们的对称轴.
2.观察对称轴的交点有何共同点?交点到顶点的距离怎样?正多边形的顶点是否共圆?理解正多边形的外接圆一定存在.
3.分析对称轴与正多边形内角的关系,结合角平分线的性质思考交点到各边的距离有何关系?理解正多边形内切圆一定存在.
4.结合教材图27.4.4和27.4.5学习正多边形的相关概念(中心,中心角,半径、边心距).
5.学习怎样运用等分圆周的方法画正多边形?
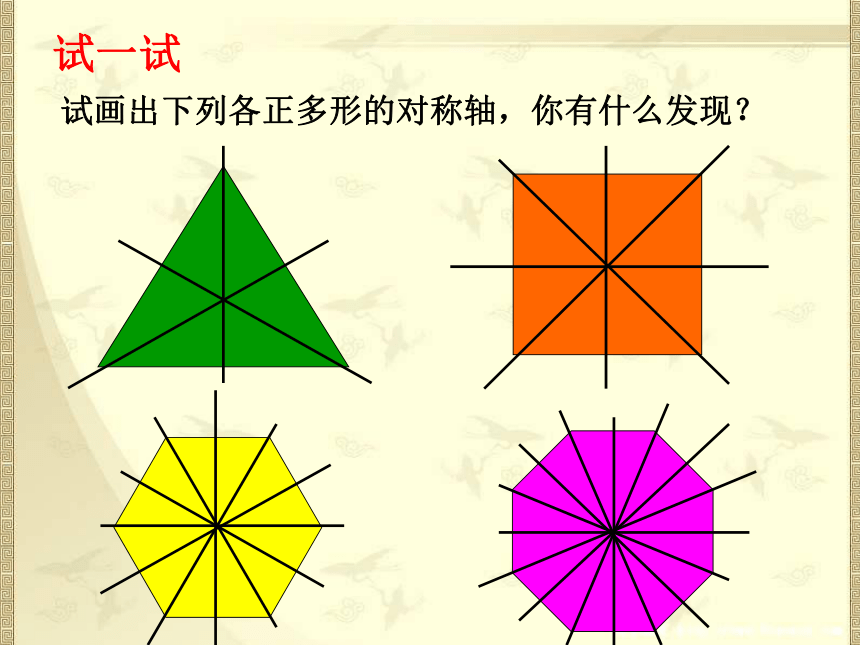
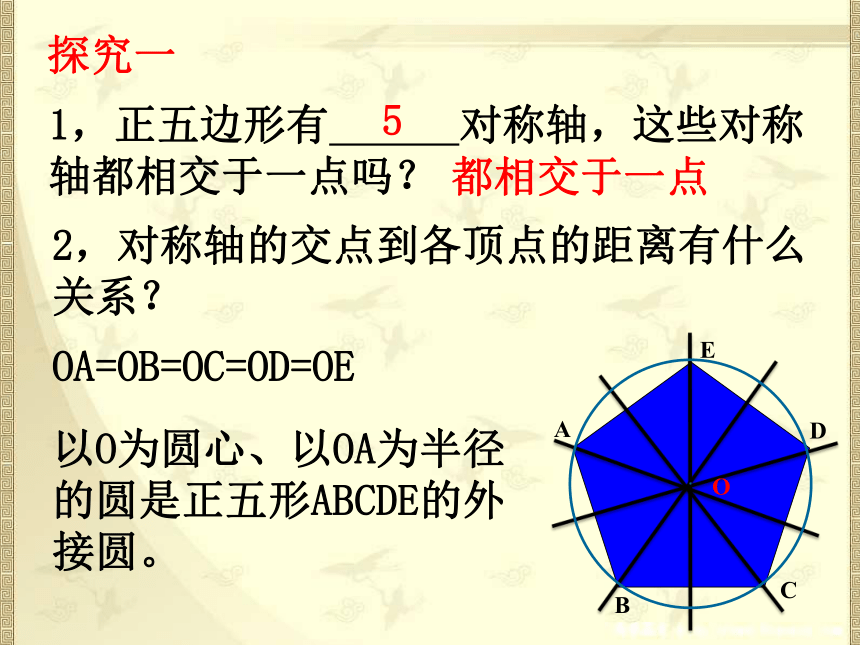
6.结合教材例题学习掌握特殊的正多边形的尺规作图. 试一试试画出下列各正多形的对称轴,你有什么发现?探究一1,正五边形有 对称轴,这些对称轴都相交于一点吗?2,对称轴的交点到各顶点的距离有什么关系?·ABCDEOOA=OB=OC=OD=OE5以O为圆心、以OA为半径的圆是正五形ABCDE的外接圆。都相交于一点探究一3,正五边形的对称轴平分正五边形的每一个内角吗?为什么?·ABCDEO角平分线有什么性质?4,对称轴交点点O到各边的距离相等吗?相等,记为r.FGHJK以O为圆心、以r为半径的圆是正五形ABCDE的内切圆。拓展其它的正多边形具有以上的性质吗?任何正多边形都有一个外接圆和一个内切圆。正多边形每一边所对的外接圆的圆心角叫做正多边形的中心角.我们把一个正多边形的外接圆和内切圆公共的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径.内切圆的半径叫做正多边形的边心距.概念学习O半径R边心距r中心角正五边形中心角多少度,外角多少度?
六边形呢?正n边形呢?正五边形
中心角360÷5=72(度)
外角 360÷5=72(度)
正六边形
中心角360÷6=60(度)
外角 360÷6=60(度)正n边形 中心角 360/n(度) 外角 360/n(度)正多边形中心角等于外角练一练∴ AB=BC=CD=DE=EA,∴ ∠A=∠B.同理∠B=∠C=∠D=∠E.∴五边形ABCDE是正五边形·探究二把圆分成n(n>2)等份,依次连结各分点所得的多边形是这个圆的一个内接正n边形。你能尺规作出圆的内接正四边形吗?·ABCDO只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形…… 典例分析:OABCEF·D 以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形……… 你能尺规作出圆的内接正六边形吗?典例分析:你还有其它的作法吗?·ABCDOE1、求出半径为R的圆内接正方形的边长,边心距和面积.课堂练习:ABCDEO2、如图:
已知点A、B、C、D、E是⊙O 的5等分点,画出⊙O的内接和外切正五边形课堂练习:3、你能作出正五边形的内切圆吗?课堂练习:这节课你学习哪些知识?小结:1、正多边形与圆的关系。2、利用正多边形与圆的关系作圆的内接正多形。反馈练习1. 下列正多边形中,对称轴条数是6条的为( )
A.正三角形B.正方形C.正六边形D.正五边形
2. 同一个圆的内接正方形与内接正六边形边长之比为 ?
3. 如图,正△ABC外接圆的半径为2,求正△ABC的边长,边心距,周长和面积.
4.用量角器画正10边形.畅谈收获
1.了解正多边形的概念、正多边形与圆的关系.
2.会等分圆周,并会画出相应的正多边形.
3.会运用尺规作图画出特殊的正多边形
2、过程与方法
1.在探究正多边形与圆的关系中,培养学生动手能力和观察分析能力.
2.通过尺规作图以及分析书写作图步骤,提高学生分析问题和语言表达能力.
3、情感、态度与价值观
1.在学生动手画图的过程中体会数学的运用价值,提高学习兴趣.
2.在分组交流中学会合作与分享. 问题1,什么样的图形是正多边形?各边相等,各角也相等的多边形是正多边形.问题2,我们学习了正多边形的哪些性质?正多形是轴对称图形.新课导入预习导航1.任意画出正三角形、正四边形、正五边形和正六边形,然后画出它们的对称轴.
2.观察对称轴的交点有何共同点?交点到顶点的距离怎样?正多边形的顶点是否共圆?理解正多边形的外接圆一定存在.
3.分析对称轴与正多边形内角的关系,结合角平分线的性质思考交点到各边的距离有何关系?理解正多边形内切圆一定存在.
4.结合教材图27.4.4和27.4.5学习正多边形的相关概念(中心,中心角,半径、边心距).
5.学习怎样运用等分圆周的方法画正多边形?
6.结合教材例题学习掌握特殊的正多边形的尺规作图. 试一试试画出下列各正多形的对称轴,你有什么发现?探究一1,正五边形有 对称轴,这些对称轴都相交于一点吗?2,对称轴的交点到各顶点的距离有什么关系?·ABCDEOOA=OB=OC=OD=OE5以O为圆心、以OA为半径的圆是正五形ABCDE的外接圆。都相交于一点探究一3,正五边形的对称轴平分正五边形的每一个内角吗?为什么?·ABCDEO角平分线有什么性质?4,对称轴交点点O到各边的距离相等吗?相等,记为r.FGHJK以O为圆心、以r为半径的圆是正五形ABCDE的内切圆。拓展其它的正多边形具有以上的性质吗?任何正多边形都有一个外接圆和一个内切圆。正多边形每一边所对的外接圆的圆心角叫做正多边形的中心角.我们把一个正多边形的外接圆和内切圆公共的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径.内切圆的半径叫做正多边形的边心距.概念学习O半径R边心距r中心角正五边形中心角多少度,外角多少度?
六边形呢?正n边形呢?正五边形
中心角360÷5=72(度)
外角 360÷5=72(度)
正六边形
中心角360÷6=60(度)
外角 360÷6=60(度)正n边形 中心角 360/n(度) 外角 360/n(度)正多边形中心角等于外角练一练∴ AB=BC=CD=DE=EA,∴ ∠A=∠B.同理∠B=∠C=∠D=∠E.∴五边形ABCDE是正五边形·探究二把圆分成n(n>2)等份,依次连结各分点所得的多边形是这个圆的一个内接正n边形。你能尺规作出圆的内接正四边形吗?·ABCDO只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形…… 典例分析:OABCEF·D 以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形……… 你能尺规作出圆的内接正六边形吗?典例分析:你还有其它的作法吗?·ABCDOE1、求出半径为R的圆内接正方形的边长,边心距和面积.课堂练习:ABCDEO2、如图:
已知点A、B、C、D、E是⊙O 的5等分点,画出⊙O的内接和外切正五边形课堂练习:3、你能作出正五边形的内切圆吗?课堂练习:这节课你学习哪些知识?小结:1、正多边形与圆的关系。2、利用正多边形与圆的关系作圆的内接正多形。反馈练习1. 下列正多边形中,对称轴条数是6条的为( )
A.正三角形B.正方形C.正六边形D.正五边形
2. 同一个圆的内接正方形与内接正六边形边长之比为 ?
3. 如图,正△ABC外接圆的半径为2,求正△ABC的边长,边心距,周长和面积.
4.用量角器画正10边形.畅谈收获
