2019年春华师大版九年级下册数学 课件:28.2 用样本估计整体 共27张PPT
文档属性
| 名称 | 2019年春华师大版九年级下册数学 课件:28.2 用样本估计整体 共27张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 251.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-13 15:51:00 | ||
图片预览








文档简介
课件27张PPT。28.2用样本估计整体目标引领1、知识与技能
1.知道简单随机抽样的概念,会进行简单随机抽样.
2.会分析简单随机抽样的可靠性,能用样本估计总体.
2、过程与方法
1.通过进行简单随机抽样并用样本估计总体,培养学生的统计意识和分析能力.
2.在实际问题的解决中培养学生的应用能力.
3、情感、态度与价值观
1.在问题探究解决中,体会特殊与一般的辩证关系.
2.在解决实际问题中体会统计的价值,养成学数学用数学的习惯. 温故知新1.什么是普查?什么是抽样调查?
2.什么是总体、个体、样本和样本容量?
3.样本的选取要注意哪些问题? 1、妈妈为了知道饼熟了没有,从刚出锅的饼上切下一小块尝尝,如果这一小块饼熟了,那么可以估计整张饼也熟了. 下面几个例子,要用怎样的调查方法?2、 环境监测中心为了了解一个城市的空气质量情况,会在这个城市中分散地选定几个点,从各地点采集数据,对这些数据进行分析,就可以估计整个城市的空气质量.?3、农科站要了解农田中某种病虫害的灾情,会随意地选定几块地,仔细检查虫卵数,然后估计一公顷农田大约平均有多少虫卵,会不会发生病虫害. 以上几个例子都不适宜做普查,而需要做抽样调查.新课引入为了使被抽查的样本能更好地反映总体,那么样本应该具备什么要求?(1)具有代表性;(2)不偏向总体中的某些个体。用抽签的办法决定哪些个体进入样本,这种理想的抽样办法称为简单的随机抽样. 请联系实际归纳简单随机抽样的步骤 .①将每个个体编号;
②将编好号的签放入盒子;
③搅拌均匀;
④抽签,把抽出的这个编号所代表的个体选入样本.探究一学生自学课本P86—P87页活动1小结:抽样之前,我们不能预测到哪些个体会被抽中,像这样不能够事先预测结果的特性叫做随机性.自主学习问题1:为了解居民对实施峰谷分时电价的意见,调查朝阳新村100户居民.这里的总体和样本分别是什么? 总体:全体居民对实施峰谷分时电价的意见
个体:100户居民对实施峰谷分时电价的意见问题2 老师布置给每个小组一个任务,用抽样调查的方法估计全班同学的平均身高.坐在教室最后面的小胖为了争速度,立即就近向他周围的三个同学作调查,计算出他们四个人的平均身高后就举手向老师示意已经完成任务了.请问:他这样的抽样调查合适吗? ?不合适课堂练习问题3 甲同学说:“6, 6, 6…啊!真的是6!你只要一直想某个数,就会掷出那个数.” ?
乙同学说:“不对,我发现我越是想要某个数就越得不到这个数,倒是不想它反而会掷出那个数.” ?请问:这两位同学的说法正确吗?为什么?不正确问题4
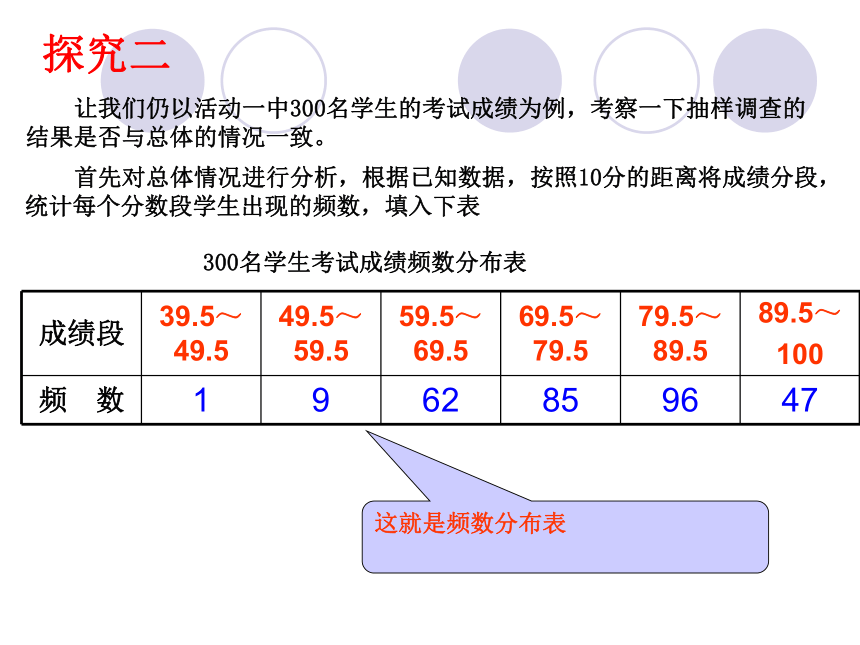
为调查一个省的环境污染情况,调查省会城市的环境污染情况.不正确课堂练习 让我们仍以活动一中300名学生的考试成绩为例,考察一下抽样调查的结果是否与总体的情况一致。 首先对总体情况进行分析,根据已知数据,按照10分的距离将成绩分段,统计每个分数段学生出现的频数,填入下表300名学生考试成绩频数分布表这就是频数分布表探究二根据上表绘制直方图300名学生成绩频数分布直方图总体的平均成绩为78.1,标准差为10.8分 从图表中可以清楚地看出79.5分到89.5分这个分数段的学生数最多,90分以上的同学较少,不及格的学生数最少。 这就是频率分布直方图做一做 活动1中,我们用简单的随机抽样方法,已经得到了第一个样本,这5个随机数如下表:列这个样本的频数分布直方图、平均成绩和方差。重复上述步骤,再取第二和第三个样本。做一做它的频数分布直方图、平均成绩和标准差分别如下:样本平均成绩为78分,方差为100.4分 做一做另外,同学们也分别选取了一些样本,它们同样也包含五个个体,如下表:同样,也可以作出这两个样本的频数分布直方图、计算它们的平均成绩和标准差,如下图所示: 做一做样本平均成绩为80.8分,
方差为42.16样本平均成绩为74.2分,
方差为14.56 5名学生成绩频数分布直方图第二样本第三样本5名学生成绩频数分布直方图 从以上三张图比较来看,它们之间存在明显的差异,平均数和标准差与总体的平均数与标准差也相去甚远,显然这样选择的样本不能反映总体的特性,是不可靠的。小结样本平均成绩为79.7分,方差为88.41 让我们再用大一些的样本试一试,这次每个样本含有10个个体。探究三10名学生成绩频数分布直方图第二样本样本平均成绩为83.3分,方差为132.61 我们继续用随机抽样方法,得到第一个样本,重复上述步骤,再取第二个样本。图30.2.4是根据小明取到的样本数据得到的频数分布直方图。做一做 再选取一些含有10名学生的样本,我们发现此时不同样本的平均成绩和标准差似乎比较接近总体的平均成绩78.1分和标准差10.8分。看来用大一些的样本来估计总体会比较可靠一点,让我们再用更大一些的样本试一试,这次每个样本含有40个个体。做一做样本平均成绩为75.65分,方差为103.5275 40名学生成绩频数分布直方图第二样本样本平均成绩为77.1分,方差为114.49 再选取一些含有40名学生的样本,我们发现此时不同样本的平均成绩和标准差与总体的平均成绩和标准差的差距更小了!(相当接近总体的平均成绩78.1)你们从自己的抽样过程中是否也得出了同样的结果?试一试小试牛刀1、请同学们在300名学生的成绩中用随机抽样的方法选取两个含有20个个体的样本,并计算出它们的平均数与方差,绘制频数分布直方图,并与总体的平均数、方差比较。 2、为了检查一批手榴弹的杀伤半径,抽取了其中20颗做试验,得到这20颗手榴弹的杀伤半径,并列表如下:课堂练习:(1)在这个问题中,总体、个体、样本和样本容量各是什么?
(2)求出这20颗手榴弹的杀伤半径的众数、中位数和平均数,并估计这批手榴弹的平均杀伤半径.解:(1)总体是要检查的这批手榴弹的杀伤半径的全体;个体是每一颗手榴弹的杀伤半径;样本是所抽取的20颗手榴弹的杀伤半径;样本容量是20.
(2)在20个数据中,10出现了6次,次数最多,所以众数是10(米).
20个数据从小到大排列,第10个和第11个数据是最中间的两个数,分别为9(米)和10(米),所以中位数是9.5 (米).样本平均数9.4(米) 当样本中个体太少时,样本的平均数、方差往往差距较大,如果选取适当的样本的个体数,各个样本的平均数、方差与总体的方差相当接近。 归纳学以致用1.要调查某校学生周日的睡眠时间,下列选项调查对象中最合适的是( )A.选取一个班级的学生B.选取50名男生
C.选取50名女生D.在该校各年级中随机选取50名学生
2.下列抽样调查:①小华为了知道烤箱中所烤的面包是否熟了,取出一小块品尝;②小明为了了解初中三个年级学生的平均身高,在七年级抽取一个班的学生做调查;③小琪为了了解北京市2012年的平均气温,上网查询了2012年7月份31天的气温情况;④小智为了了解初中三个年级学生的平均体重,在七年级、八年级、九年级各抽一个班的学生进行调查.较科学的是 .3. 某校抽检60个学生的体重如下(单位:kg) 38??32??39??40??35??45??37??38??40??29 39??41??37??42??39??34??36??39??42??36 44??33??29??40??35??39??37??46??39??31 39??36??42??38??41??36??44??34??38??38 41??39??39??34??36??48??30??39??37??42 42??45??34??48??43??35??39??44??43??44
根据以上数据绘制频数分布表和频数分布直方图,并估计全校2000名学生中,40kg以上的大约有多少人. 畅谈收获
1.知道简单随机抽样的概念,会进行简单随机抽样.
2.会分析简单随机抽样的可靠性,能用样本估计总体.
2、过程与方法
1.通过进行简单随机抽样并用样本估计总体,培养学生的统计意识和分析能力.
2.在实际问题的解决中培养学生的应用能力.
3、情感、态度与价值观
1.在问题探究解决中,体会特殊与一般的辩证关系.
2.在解决实际问题中体会统计的价值,养成学数学用数学的习惯. 温故知新1.什么是普查?什么是抽样调查?
2.什么是总体、个体、样本和样本容量?
3.样本的选取要注意哪些问题? 1、妈妈为了知道饼熟了没有,从刚出锅的饼上切下一小块尝尝,如果这一小块饼熟了,那么可以估计整张饼也熟了. 下面几个例子,要用怎样的调查方法?2、 环境监测中心为了了解一个城市的空气质量情况,会在这个城市中分散地选定几个点,从各地点采集数据,对这些数据进行分析,就可以估计整个城市的空气质量.?3、农科站要了解农田中某种病虫害的灾情,会随意地选定几块地,仔细检查虫卵数,然后估计一公顷农田大约平均有多少虫卵,会不会发生病虫害. 以上几个例子都不适宜做普查,而需要做抽样调查.新课引入为了使被抽查的样本能更好地反映总体,那么样本应该具备什么要求?(1)具有代表性;(2)不偏向总体中的某些个体。用抽签的办法决定哪些个体进入样本,这种理想的抽样办法称为简单的随机抽样. 请联系实际归纳简单随机抽样的步骤 .①将每个个体编号;
②将编好号的签放入盒子;
③搅拌均匀;
④抽签,把抽出的这个编号所代表的个体选入样本.探究一学生自学课本P86—P87页活动1小结:抽样之前,我们不能预测到哪些个体会被抽中,像这样不能够事先预测结果的特性叫做随机性.自主学习问题1:为了解居民对实施峰谷分时电价的意见,调查朝阳新村100户居民.这里的总体和样本分别是什么? 总体:全体居民对实施峰谷分时电价的意见
个体:100户居民对实施峰谷分时电价的意见问题2 老师布置给每个小组一个任务,用抽样调查的方法估计全班同学的平均身高.坐在教室最后面的小胖为了争速度,立即就近向他周围的三个同学作调查,计算出他们四个人的平均身高后就举手向老师示意已经完成任务了.请问:他这样的抽样调查合适吗? ?不合适课堂练习问题3 甲同学说:“6, 6, 6…啊!真的是6!你只要一直想某个数,就会掷出那个数.” ?
乙同学说:“不对,我发现我越是想要某个数就越得不到这个数,倒是不想它反而会掷出那个数.” ?请问:这两位同学的说法正确吗?为什么?不正确问题4
为调查一个省的环境污染情况,调查省会城市的环境污染情况.不正确课堂练习 让我们仍以活动一中300名学生的考试成绩为例,考察一下抽样调查的结果是否与总体的情况一致。 首先对总体情况进行分析,根据已知数据,按照10分的距离将成绩分段,统计每个分数段学生出现的频数,填入下表300名学生考试成绩频数分布表这就是频数分布表探究二根据上表绘制直方图300名学生成绩频数分布直方图总体的平均成绩为78.1,标准差为10.8分 从图表中可以清楚地看出79.5分到89.5分这个分数段的学生数最多,90分以上的同学较少,不及格的学生数最少。 这就是频率分布直方图做一做 活动1中,我们用简单的随机抽样方法,已经得到了第一个样本,这5个随机数如下表:列这个样本的频数分布直方图、平均成绩和方差。重复上述步骤,再取第二和第三个样本。做一做它的频数分布直方图、平均成绩和标准差分别如下:样本平均成绩为78分,方差为100.4分 做一做另外,同学们也分别选取了一些样本,它们同样也包含五个个体,如下表:同样,也可以作出这两个样本的频数分布直方图、计算它们的平均成绩和标准差,如下图所示: 做一做样本平均成绩为80.8分,
方差为42.16样本平均成绩为74.2分,
方差为14.56 5名学生成绩频数分布直方图第二样本第三样本5名学生成绩频数分布直方图 从以上三张图比较来看,它们之间存在明显的差异,平均数和标准差与总体的平均数与标准差也相去甚远,显然这样选择的样本不能反映总体的特性,是不可靠的。小结样本平均成绩为79.7分,方差为88.41 让我们再用大一些的样本试一试,这次每个样本含有10个个体。探究三10名学生成绩频数分布直方图第二样本样本平均成绩为83.3分,方差为132.61 我们继续用随机抽样方法,得到第一个样本,重复上述步骤,再取第二个样本。图30.2.4是根据小明取到的样本数据得到的频数分布直方图。做一做 再选取一些含有10名学生的样本,我们发现此时不同样本的平均成绩和标准差似乎比较接近总体的平均成绩78.1分和标准差10.8分。看来用大一些的样本来估计总体会比较可靠一点,让我们再用更大一些的样本试一试,这次每个样本含有40个个体。做一做样本平均成绩为75.65分,方差为103.5275 40名学生成绩频数分布直方图第二样本样本平均成绩为77.1分,方差为114.49 再选取一些含有40名学生的样本,我们发现此时不同样本的平均成绩和标准差与总体的平均成绩和标准差的差距更小了!(相当接近总体的平均成绩78.1)你们从自己的抽样过程中是否也得出了同样的结果?试一试小试牛刀1、请同学们在300名学生的成绩中用随机抽样的方法选取两个含有20个个体的样本,并计算出它们的平均数与方差,绘制频数分布直方图,并与总体的平均数、方差比较。 2、为了检查一批手榴弹的杀伤半径,抽取了其中20颗做试验,得到这20颗手榴弹的杀伤半径,并列表如下:课堂练习:(1)在这个问题中,总体、个体、样本和样本容量各是什么?
(2)求出这20颗手榴弹的杀伤半径的众数、中位数和平均数,并估计这批手榴弹的平均杀伤半径.解:(1)总体是要检查的这批手榴弹的杀伤半径的全体;个体是每一颗手榴弹的杀伤半径;样本是所抽取的20颗手榴弹的杀伤半径;样本容量是20.
(2)在20个数据中,10出现了6次,次数最多,所以众数是10(米).
20个数据从小到大排列,第10个和第11个数据是最中间的两个数,分别为9(米)和10(米),所以中位数是9.5 (米).样本平均数9.4(米) 当样本中个体太少时,样本的平均数、方差往往差距较大,如果选取适当的样本的个体数,各个样本的平均数、方差与总体的方差相当接近。 归纳学以致用1.要调查某校学生周日的睡眠时间,下列选项调查对象中最合适的是( )A.选取一个班级的学生B.选取50名男生
C.选取50名女生D.在该校各年级中随机选取50名学生
2.下列抽样调查:①小华为了知道烤箱中所烤的面包是否熟了,取出一小块品尝;②小明为了了解初中三个年级学生的平均身高,在七年级抽取一个班的学生做调查;③小琪为了了解北京市2012年的平均气温,上网查询了2012年7月份31天的气温情况;④小智为了了解初中三个年级学生的平均体重,在七年级、八年级、九年级各抽一个班的学生进行调查.较科学的是 .3. 某校抽检60个学生的体重如下(单位:kg) 38??32??39??40??35??45??37??38??40??29 39??41??37??42??39??34??36??39??42??36 44??33??29??40??35??39??37??46??39??31 39??36??42??38??41??36??44??34??38??38 41??39??39??34??36??48??30??39??37??42 42??45??34??48??43??35??39??44??43??44
根据以上数据绘制频数分布表和频数分布直方图,并估计全校2000名学生中,40kg以上的大约有多少人. 畅谈收获
