人教版九年级上册第二十二章 二次函数解析式求法复习课教学课件 共28张PPT
文档属性
| 名称 | 人教版九年级上册第二十二章 二次函数解析式求法复习课教学课件 共28张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 719.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-13 00:00:00 | ||
图片预览

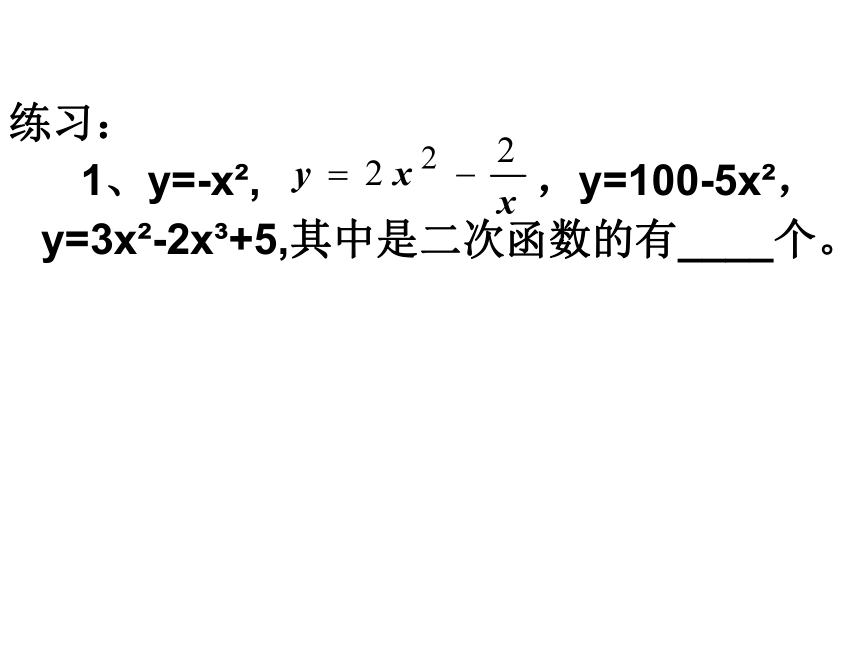


文档简介
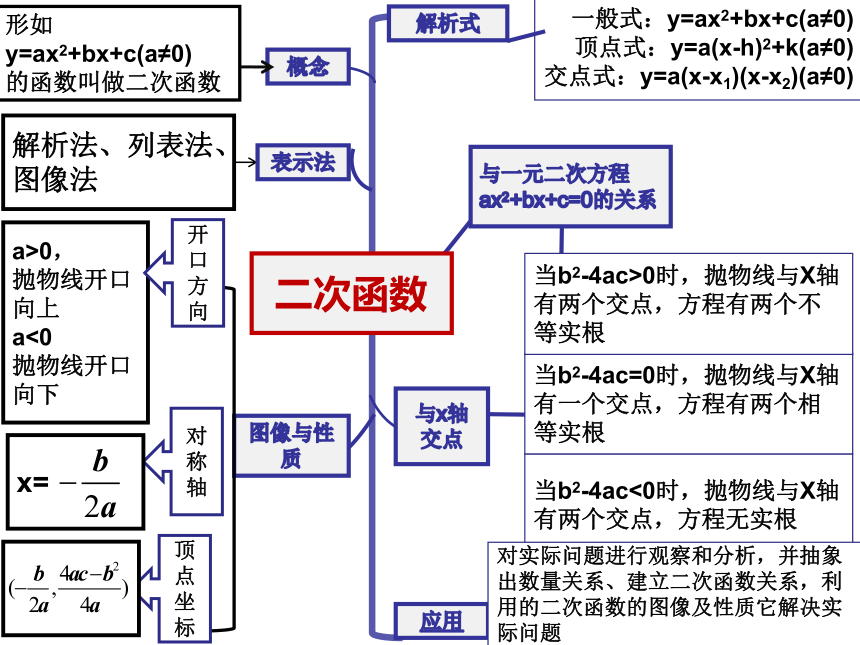
课件28张PPT。学习如登山二次函数复习课应用 二次函数a>0,
抛物线开口向上
a<0
抛物线开口向下一般式:y=ax2+bx+c(a≠0)
顶点式:y=a(x-h)2+k(a≠0)
交点式:y=a(x-x1)(x-x2)(a≠0)当b2-4ac=0时,抛物线与X轴有一个交点,方程有两个相等实根当b2-4ac<0时,抛物线与X轴有两个交点,方程无实根对实际问题进行观察和分析,并抽象出数量关系、建立二次函数关系,利用的二次函数的图像及性质它解决实际问题当b2-4ac>0时,抛物线与X轴有两个交点,方程有两个不等实根练习:
1、y=-x2, ,y=100-5x2,y=3x2-2x3+5,其中是二次函数的有____个。2.函数 (其中a、b、c为常数),当a、b、c满足什么条件时,
(1)它是二次函数;
(2)它是一次函数;
(3)它是正比例函数;3.当m=______时,函数
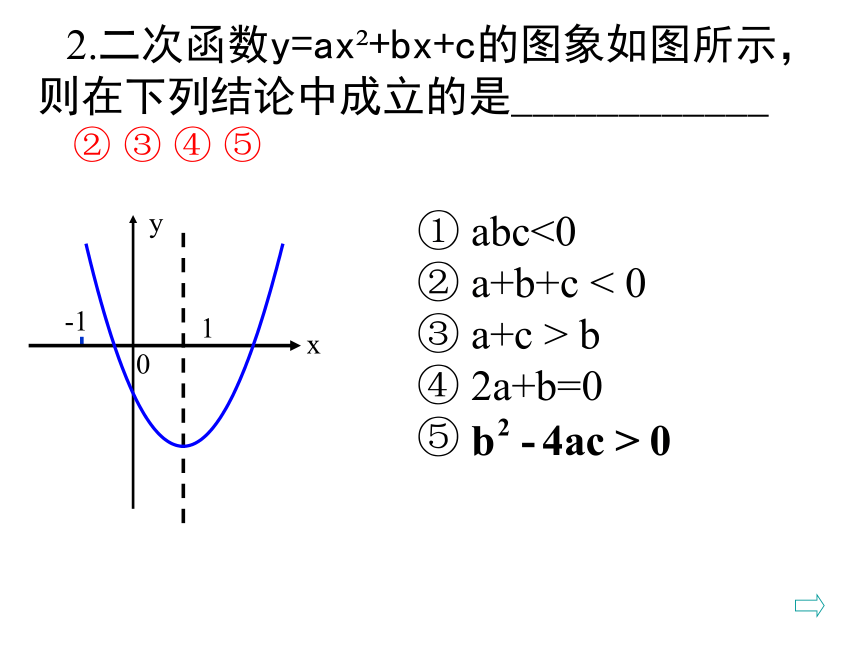
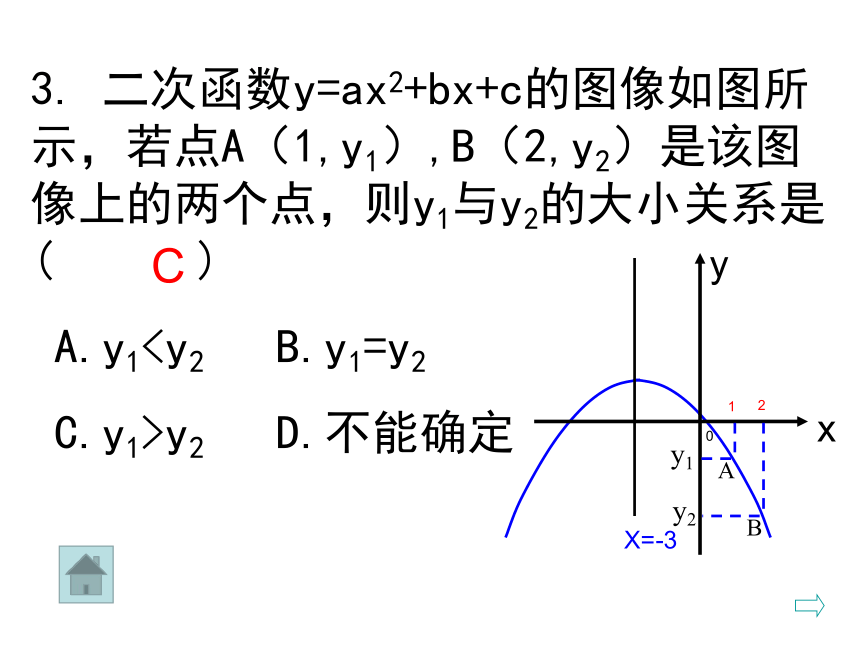
是二次函数?考考你 2.二次函数y=ax2+bx+c的图象如图所示,则在下列结论中成立的是____________②③④⑤3. 二次函数y=ax2+bx+c的图像如图所示,若点A(1,y1),B(2,y2)是该图像上的两个点,则y1与y2的大小关系是( )
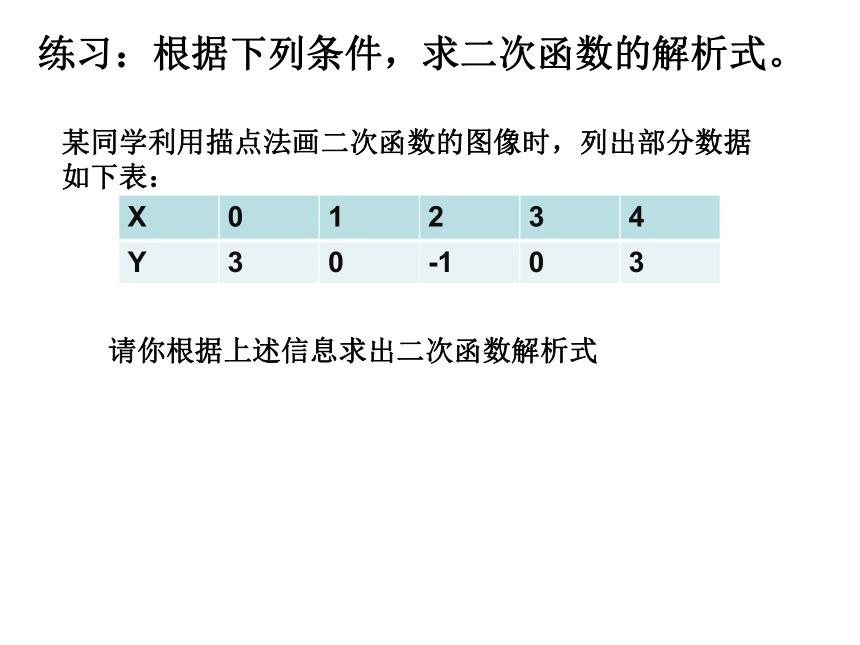
A.y1 C.y1>y2 D.不能确定C12y1y2AB练习:根据下列条件,求二次函数的解析式。某同学利用描点法画二次函数的图像时,列出部分数据如下表:请你根据上述信息求出二次函数解析式已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的解析式.解:抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
? a=1或-1
又 顶点在直线x=1上,且顶点到x轴的距离为5,
? 顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
展开成一般式即可.
小结:一般地,抛物线 y = ax2与y = ±a(x-h)2+k形状相同,
位置不同。与x轴有两个不
同的交点
(x1,0)
(x2,0)有两个不同的解x=x1,x=x2b2-4ac>0与x轴有唯一个
交点有两个相等的解
x1=x2=b2-4ac=0与x轴没有
交点没有实数根b2-4ac<01.一元二次方程 3x2+x-10=0的两个根是
x1=2 ,x2= , 那么二次函数y=3x2+x-10与
x轴的交点坐标是 .
2.结合二次函数y=ax2+bx+c图象,解答下列问题:
①写出方程ax2+bx+c=0的根;
②写出不等式ax2+bx+c>0的解集;
③写出y随x的增大而减小的自变量x的取值范围;
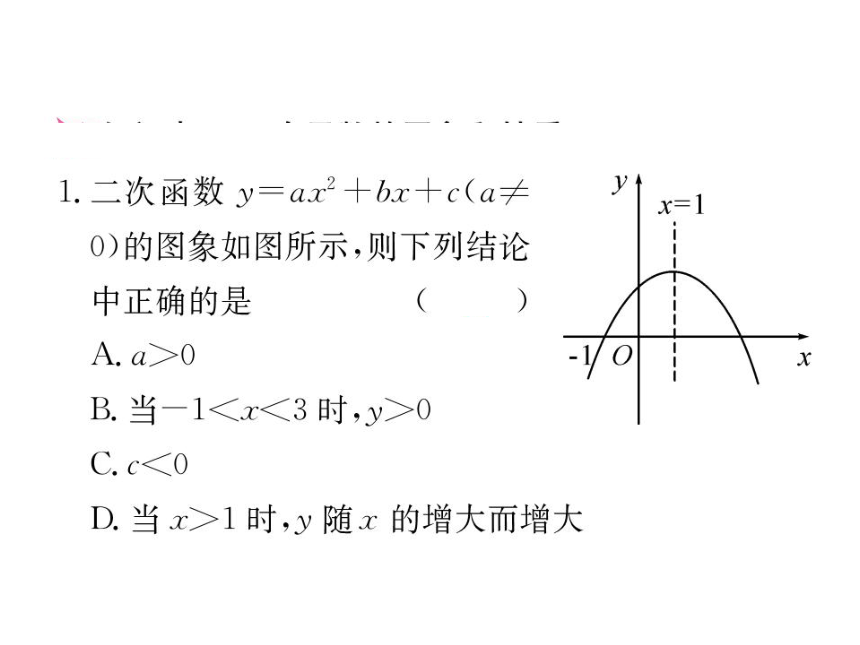
3.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m= ,此时抛物线 y=x2-2x+m与x轴有 个交点.4.已知抛物线 y=x2–8x+c的顶点在 x轴上,则c= .1116 5.已知抛物线y = ax2+bx+c的图象如图,则关于x的方程ax2 + bx + c-3 = 0根的情况是( )
A. 有两个不相等的实数根
B. 有两个异号的实数根
C. 有两个相等的实数根
D. 没有实数根xA1.3.变式训练: 已知抛物线y=ax2+bx+c的图象如图所示,则关于x的方程 ax2+bx+c-8=0的根的情况是( )
A.有两个不相等的正实数根
B.有两个异号实数根
C.有两个相等的实数根
D.没有实数根C
2 .如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,
点P从点A开始沿AB边向点B以2厘米/秒的速度移动,
点Q从点B开始沿BC边向点C以1厘米/秒的速度
移动,如果P,Q分别从A,B同时出发,
几秒后ΔPBQ的面积最大?
最大面积是多少?PQ解:根据题意,设经过x秒后ΔPBQ的面积y最大AP=2x cm PB=(8-2x ) cm QB=x cm则 y= x(8-2x)=-x2 +4x=-(x2 -4x +4 -4)= -(x - 2)2 + 4所以,当P、Q同时运动2秒后ΔPBQ的面积y最大
最大面积是 4 cm2(0(500-10x) 个
(2)一个商品所获利润可以表示为(50+x-40)元(4)共获利润可以表示为(50+x-40)(500-10x)元3:某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?分析:利润=(每件商品所获利润)× (销售件数) 设每个涨价x元, 那么(3)销售量可以表示为(1)销售价可以表示为(50+x)元(x≥ 0)
(500-10x) 个
(2)一个商品所获利润可以表示为(50+x-40)元(4)共获利润可以表示为(50+x-40)(500-10x)元214、a,b,c符号的确定抛物线y=ax2+bx+c的符号问题:(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)C的符号:由抛物线与y轴的交点位置确定.交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0(3)b的符号:由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<01、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c的符号为( )
A、a<0,b>0,c>0 B、a<0,b>0,c<0
C、a<0,b<0,c>0 D、a<0,b<0,c<0 2、二次函数y=ax2+bx+c(a≠0)的图象
如图所示,则a、b、c的符号为( )
A、a>0,b>0,c=0 B、a<0,b>0,c=0
C、a<0,b<0,c<0 D、a>0,b<0,c=0 3、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c 、 △的符号为( )
A、a>0,b=0,c>0,△>0 B、a<0,b>0,c<0,△=0
C、a>0,b=0,c<0,△>0 D、a<0,b=0,c<0,△<0 BACooo练习:熟练掌握a,b, c,△与抛物线图象的关系(上正、下负)(左同、右异) ·c4.抛物线y=ax2+bx+c(a≠0)的图象经过原点和
二、三、四象限,判断a、b、c的符号情况:
a 0,b 0,c 0.
<=<5.抛物线y=ax2+bx+c(a≠0)的图象经过原点,
且它的顶点在第三象限,则a、b、c满足
的条件是:a 0,b 0,c 0. >=6.二次函数y=ax2+bx+c中,如果a>0,b<0,c<0,
那么这个二次函数图象的顶点必在第 象限 先根据题目的要求画出函数的草图,再根据
图象以及性质确定结果(数形结合的思想)四>
抛物线开口向上
a<0
抛物线开口向下一般式:y=ax2+bx+c(a≠0)
顶点式:y=a(x-h)2+k(a≠0)
交点式:y=a(x-x1)(x-x2)(a≠0)当b2-4ac=0时,抛物线与X轴有一个交点,方程有两个相等实根当b2-4ac<0时,抛物线与X轴有两个交点,方程无实根对实际问题进行观察和分析,并抽象出数量关系、建立二次函数关系,利用的二次函数的图像及性质它解决实际问题当b2-4ac>0时,抛物线与X轴有两个交点,方程有两个不等实根练习:
1、y=-x2, ,y=100-5x2,y=3x2-2x3+5,其中是二次函数的有____个。2.函数 (其中a、b、c为常数),当a、b、c满足什么条件时,
(1)它是二次函数;
(2)它是一次函数;
(3)它是正比例函数;3.当m=______时,函数
是二次函数?考考你 2.二次函数y=ax2+bx+c的图象如图所示,则在下列结论中成立的是____________②③④⑤3. 二次函数y=ax2+bx+c的图像如图所示,若点A(1,y1),B(2,y2)是该图像上的两个点,则y1与y2的大小关系是( )
A.y1
? a=1或-1
又 顶点在直线x=1上,且顶点到x轴的距离为5,
? 顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
展开成一般式即可.
小结:一般地,抛物线 y = ax2与y = ±a(x-h)2+k形状相同,
位置不同。与x轴有两个不
同的交点
(x1,0)
(x2,0)有两个不同的解x=x1,x=x2b2-4ac>0与x轴有唯一个
交点有两个相等的解
x1=x2=b2-4ac=0与x轴没有
交点没有实数根b2-4ac<01.一元二次方程 3x2+x-10=0的两个根是
x1=2 ,x2= , 那么二次函数y=3x2+x-10与
x轴的交点坐标是 .
2.结合二次函数y=ax2+bx+c图象,解答下列问题:
①写出方程ax2+bx+c=0的根;
②写出不等式ax2+bx+c>0的解集;
③写出y随x的增大而减小的自变量x的取值范围;
3.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m= ,此时抛物线 y=x2-2x+m与x轴有 个交点.4.已知抛物线 y=x2–8x+c的顶点在 x轴上,则c= .1116 5.已知抛物线y = ax2+bx+c的图象如图,则关于x的方程ax2 + bx + c-3 = 0根的情况是( )
A. 有两个不相等的实数根
B. 有两个异号的实数根
C. 有两个相等的实数根
D. 没有实数根xA1.3.变式训练: 已知抛物线y=ax2+bx+c的图象如图所示,则关于x的方程 ax2+bx+c-8=0的根的情况是( )
A.有两个不相等的正实数根
B.有两个异号实数根
C.有两个相等的实数根
D.没有实数根C
2 .如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,
点P从点A开始沿AB边向点B以2厘米/秒的速度移动,
点Q从点B开始沿BC边向点C以1厘米/秒的速度
移动,如果P,Q分别从A,B同时出发,
几秒后ΔPBQ的面积最大?
最大面积是多少?PQ解:根据题意,设经过x秒后ΔPBQ的面积y最大AP=2x cm PB=(8-2x ) cm QB=x cm则 y= x(8-2x)=-x2 +4x=-(x2 -4x +4 -4)= -(x - 2)2 + 4所以,当P、Q同时运动2秒后ΔPBQ的面积y最大
最大面积是 4 cm2(0
(2)一个商品所获利润可以表示为(50+x-40)元(4)共获利润可以表示为(50+x-40)(500-10x)元3:某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?分析:利润=(每件商品所获利润)× (销售件数) 设每个涨价x元, 那么(3)销售量可以表示为(1)销售价可以表示为(50+x)元(x≥ 0)
(500-10x) 个
(2)一个商品所获利润可以表示为(50+x-40)元(4)共获利润可以表示为(50+x-40)(500-10x)元214、a,b,c符号的确定抛物线y=ax2+bx+c的符号问题:(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)C的符号:由抛物线与y轴的交点位置确定.交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0(3)b的符号:由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<01、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c的符号为( )
A、a<0,b>0,c>0 B、a<0,b>0,c<0
C、a<0,b<0,c>0 D、a<0,b<0,c<0 2、二次函数y=ax2+bx+c(a≠0)的图象
如图所示,则a、b、c的符号为( )
A、a>0,b>0,c=0 B、a<0,b>0,c=0
C、a<0,b<0,c<0 D、a>0,b<0,c=0 3、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c 、 △的符号为( )
A、a>0,b=0,c>0,△>0 B、a<0,b>0,c<0,△=0
C、a>0,b=0,c<0,△>0 D、a<0,b=0,c<0,△<0 BACooo练习:熟练掌握a,b, c,△与抛物线图象的关系(上正、下负)(左同、右异) ·c4.抛物线y=ax2+bx+c(a≠0)的图象经过原点和
二、三、四象限,判断a、b、c的符号情况:
a 0,b 0,c 0.
<=<5.抛物线y=ax2+bx+c(a≠0)的图象经过原点,
且它的顶点在第三象限,则a、b、c满足
的条件是:a 0,b 0,c 0. >=6.二次函数y=ax2+bx+c中,如果a>0,b<0,c<0,
那么这个二次函数图象的顶点必在第 象限 先根据题目的要求画出函数的草图,再根据
图象以及性质确定结果(数形结合的思想)四>
同课章节目录
