第10章 相交线、平行线和平移单元检测试卷(含解析)
文档属性
| 名称 | 第10章 相交线、平行线和平移单元检测试卷(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-13 00:00:00 | ||
图片预览




文档简介
沪科版七年级下第10相交线、平行线和平移单元检测试卷
班级_____________考号______________姓名_______________总分_________________
一、选择题(12小题,每题3分,共36分)
1.如图各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
2.如图,直线AB和CD相交于O,那么图中 ∠DOE与∠COA 的关系是( )
A.对顶角 B.相等 C.互余 D.互补
3.如图,在△ABC中,∠C=90°,AC=4,点P是边BC上的动点,则AP的长不可能( )
A.3 B.4 C.5 D.6
4.下列说法正确的是( )
A.同旁内角互补
B.相等的角是对顶角
C.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
D.经过直线外一点,有且只有一条直线与已知直线平行
5.如图,已知直线AD、BE、CF相交于点O,OG⊥AD,且∠BOC=35°,∠FOG=30°,则∠DOE的度数为( )
A. B. C. D.
6.如图,下列条件中,不能判断直线的是( )
A. B. C. D.
7.一学员在广场上练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )
A.第一次向左拐30°,第二次向右拐30°
B.第一次向右拐50°,第二次向左拐130°
C.第一次向左拐50°,第二次向右拐130°
D.第一次向左拐50°,第二次向左拐130
8.如图,AB∥CD,直线EF分别交AB,CD于E,F,EG平分∠BEF.若∠1=72°,则∠2是( )度.
A.54 B.72 C.36 D.144.
9.如图,直线,,,则的度数是( )
A. B. C. D.
10.将一副三角板按如图的所示放置,下列结论中不正确的是( )
A.若,则有;
B.;
C.若,则有;
D.如果,必有.
11.如图,AB∥EF∥CD,点G在AB上,GE∥BC,GE的延长线交DC的延长线于点H,则图中与∠AGE相等的角共有( )
A.6个 B.5个 C.4个 D.3个
12.如图,在直角三角形ABC中,∠BAC=90°,AB=3,AC=4,将三角形ABC沿直线BC向右平移2.5个单位长度得到三角形DEF,连接AD,AE.有下列结论:①AC∥DF;②AD∥BE,AD=BE;③∠ABE=∠DEF;④ED⊥AC.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(6小题,每题3分,共18分)
13.如图,∠PQR=138°.SQ⊥QR于Q,QT⊥PQ于Q,则∠SQT等于______.
14.如图,AB∥CD,FB平分∠EFD,若∠B=32°,则∠1的度数是________.
15.如图,给出如下推理:①∠1=∠3.∴AD∥BC;②∠A+∠1+∠2=180°,∴AB∥CD;③∠A+∠3+∠4=180°,∴AB∥CD;④∠2=∠4,∴AD∥BC.其中正确的推理有_____.(填序号)
16.如图,直线 a∥b,直线 l 与 a,b 分别交于A、B 两点,过点B 作 BC⊥AB 交直线 a 于点 C,若∠1=65°,则∠2=_________
17.如图,已知,,点C在BO上,点E在OD的延长线上,若,,则的度数是______
18.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,,平移距离为6,则阴影部分面积为________.
三、解答题(8小题,共66分)
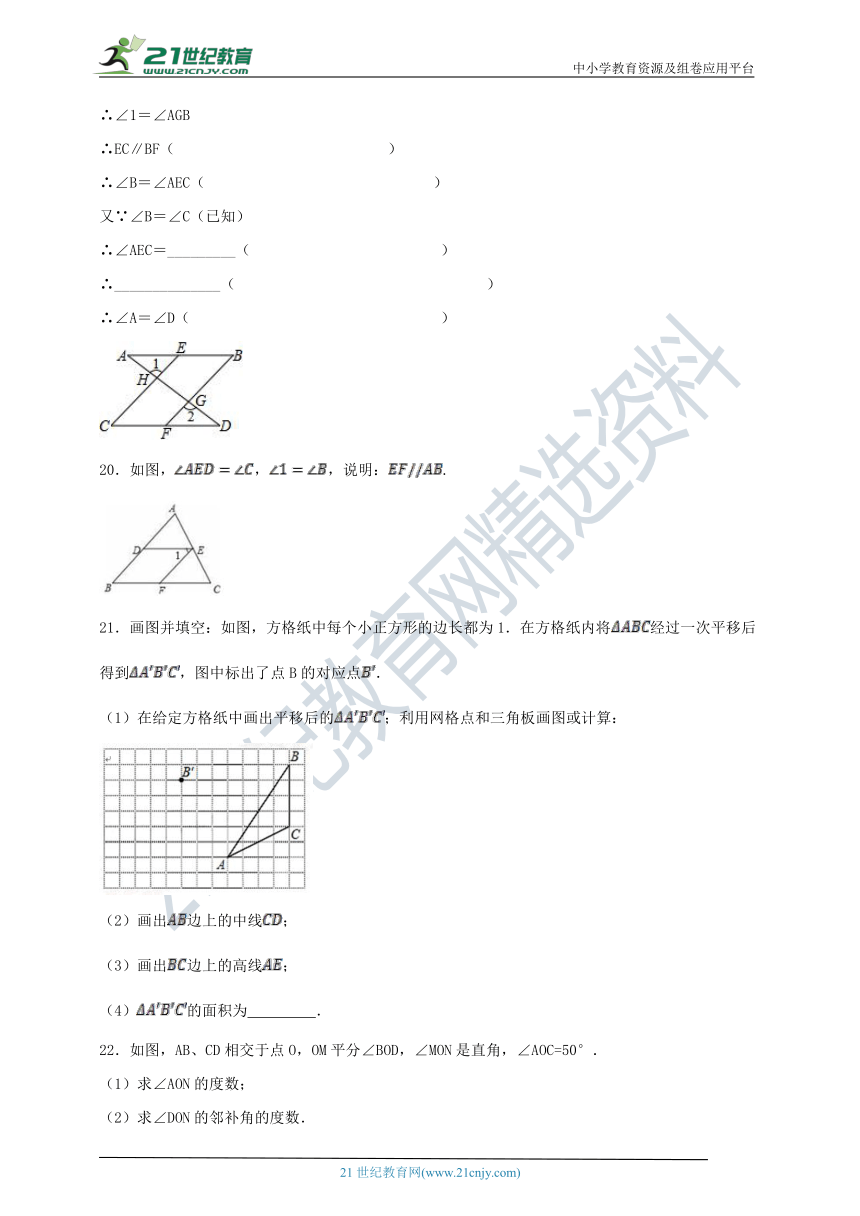
19.完成下面的证明过程:如图所示,直线AD与AB、CD分别相交于点A、D,与EC、BF分别相交于点H、G,已知∠1=∠2,∠B=∠C
求证:∠A=∠D
证明:∵∠1=∠2(已知),∠2=∠AGB( )
∴∠1=∠AGB
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC=_________( )
∴______________( )
∴∠A=∠D( )
20.如图,,,说明:.
21.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将经过一次平移后得到,图中标出了点B的对应点.
(1)在给定方格纸中画出平移后的;利用网格点和三角板画图或计算:
(2)画出边上的中线;
(3)画出边上的高线;
(4)的面积为 .
22.如图,AB、CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°.
(1)求∠AON的度数;
(2)求∠DON的邻补角的度数.
23.如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于E.
(1)求证:AD∥BC;
(2)若∠ADB=36°,求∠EFC的度数.
24.如图,AB∥CD,直线EF与AB,CD交于点G,H,GM⊥GE,∠BGM=20°,HN平分∠CHE,求∠NHD的度数.
25.如图,,,,,
(1)若设,则 °, °(用含的代数式表示);
(2)求的度数.
26.如图,已知,,点是射线上一动点(与点不重合),、分别平分和,分别交射线于点、.
(1)求的度数;
(2)当点运动时,与之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点运动到使时,求的度数.
参考答案
1.【考点】对顶角的定义
【分析】根据对顶角的定义判断即可.
解:根据两条直线相交,才能构成对顶角进行判断,
A、C、D都不是由两条直线相交构成的图形,错误,
B是由两条直线相交构成的图形,正确,
故选:B.
【点睛】本题主要考查了对顶角的定义,有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
2.【考点】垂线
【分析】先由垂直的定义得到∠AOE=∠BOE=90°,则∠DOE+∠BOD=90°,再根据对顶角相等得到∠BOD=∠AOC,所以∠DOE+∠AOC=90°,然后根据互余的定义进行判断.
解:∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∴∠DOE+∠BOD=90°,
∵∠BOD=∠AOC,
∴∠DOE+∠AOC=90°,
即∠DOE与∠COA互余.
故选:C.
【点睛】本题考查了垂线:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.垂线的性质过一点有且只有一条直线与已知直线垂直.也考查了对顶角和两角互余.
3.【考点】垂线段最短
【分析】根据垂线段最短分析即可.
解:已知,在△ABC中,∠C=90°,AC=4, 根据垂线段最短,可知AP的长不可小于4,当P和C重合时,AP=4, 故选:A.
【点睛】本题考查垂线段最短的性质,解题的关键是正确理解垂线段最短的性质.
4.【考点】平行线的性质,点到直线的距离,对顶角
【分析】依据平行线的性质、点到直线的距离以及对顶角的概念进行判断即可.
解:A、两直线平行,同旁内角才互补,故本选项错误;
B、相等的角位置关系不固定,对顶角是其中一种,故本选项错误;
C、距离是一段长度,用具体数值表示,从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离,故本选项错误;
D、经过直线外一点,有且只有一条直线与已知直线平行,故本选项正确.
故选:D.
【点睛】本题主要考查了平行线的性质、点到直线的距离以及对顶角的概念,解题时注意:点到直线的距离是一个长度,而不是一个图形,也就是垂线段的长度,而不是垂线段.
5.【考点】垂线,对顶角、邻补角
【分析】根据对顶角相等,以及垂直的定义求出所求角度数即可.
解:∵∠BOC=35°,∠FOG=30°,
∴∠EOF=∠BOC=35°,
∴∠GOE=∠GOF+∠FOE=65°,
∵OG⊥AD,
∴∠GOD=90°,
∴∠DOE=25°,
故选:D.
【点睛】此题考查了垂线,以及对顶角、邻补角,熟练掌握各自的性质是解本题的关键.
6.【考点】平行线的判定
【分析】根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行对各选项进行判断.
解:当∠1=∠3时,a∥b;
当∠4=∠5时,a∥b;
当∠2+∠4=180°时,a∥b.
故选:B.
【点睛】本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
7.【考点】平行线的判定
【分析】首先根据题意对各选项画出示意图,观察图形,根据同位角相等,两直线平行,即可得出答案.
解:如图:
故选A.
【点睛】此题考查了平行线的判定.注意数形结合法的应用,注意掌握同位角相等,两直线平行.
8.【考点】平行线的性质,角平分线的性质
【分析】根据两直线平行,同旁内角互补,内错角相等,可求出∠BEF=108°,∠2=∠BEG,然后再根据角平分线的性质可求出∠BEG,继而可求出∠2.
解:∵AB∥CD,
∴∠BEF=180°-∠1=180°-72°=108°,∠2=∠BEG,
又∵EG平分∠BEF,
∴∠2=∠BEG=∠BEF=×108°=54°,
故本题答案应为:A.
【点睛】平行线的性质和角平分线的性质是本题的考点,熟练掌握并正确运用其性质是解题的关键.
9.【考点】平行线性质
【分析】先根据平行线的性质,由l1∥l2得∠3=∠1=40°,再根据平行线的判定,由∠α=∠β得AB∥CD,然后根据平行线的性质得∠2+∠3=180°,再把∠1=40°代入计算即可.
解:如图,
∵l1∥l2,
∴∠3=∠1=40°,
∵∠α=∠β,
∴AB∥CD,
∴∠2+∠3=180°,
∴∠2=180°-∠3=180°-40°=140°.
故选:D.
【点睛】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.
10.【考点】平行线的判定与性质、余角和补角
【分析】根据两种三角板的各角的度数,利用平行线的判定与性质结合已知条件对各个结论逐一验证,即可得出答案.
解: ∵∠2=30°,
∴∠1=90°-30°=60°,
∵∠E=60°,
∴∠1=∠E,
∴AC∥DE.
∴A项正确;
∵∠1+∠2=90°,∠3+∠2=90°,
∴∠1+∠2+∠3+∠2=∠CAD+∠BAE=180°,
∴B项正确;
∵BC∥AD,
∴∠C+∠CAD=180°,
∵∠C=45°,
∴∠CAD =135°,
又∵∠CAD+∠BAE=180°,
∴∠2=∠BAE=180°-135°=45°,
∴C项错误;
∵∠CAD =150°,∠CAD+∠BAE=180°,
∴∠2=∠BAE=180°-150°=30°,
∴AC∥DE,
∴∠4=∠C,
∴D项正确;
故本题答案应为:C.
【点睛】此题主要考查了平行线的判定与性质、余角和补角的相关知识,熟练掌握两种三角板各角的度数是解题的关键.
11.【考点】平行线的性质
【分析】先由AB∥EF∥CD,根据两直线平行,内错角相等得到∠AGE=∠GEF,∠AGE=∠GHC;再由GE∥BC,根据平行线的性质,找出其它相等的角,注意做到不重不漏.
解:∵AB∥EF∥CD,
∴∠AGE=∠GEF,∠AGE=∠GHC.
∵GE∥BC,
∴∠AGE=∠ABP,∠GEF=∠BPF,∠GHC=∠BCD.
由对顶角相等,得∠BPF=∠EPC.
则与∠AGE相等的角有∠GEF,∠GHC,∠ABP,∠BPF,∠BCD,∠EPC共6个.
故选:A.
【点睛】本题考查平行线的性质,解题关键是熟练掌握:两直线平行,同位角相等,内错角相等.
12.【考点】平移的性质
【分析】根据平移的性质得到AC∥DF,AB∥DE,AD∥CF,AD=CF=2.5,∠EDF=∠BAC=90°,则利用平行线的性质得∠ABE=∠DEF,利用垂直的定义得DE⊥DF,于是根据平行线的性质可判断DE⊥AC.
解:∵将△ABC沿直线向右平移2.5个单位得到△DEF, ∴AC∥DF,AB∥DE,AD∥CF,AD=CF=2.5,∠EDF=∠BAC=90°, ∴∠ABE=∠DEF,DE⊥DF, ∴DE⊥AC, ∴①②③④都正确. 故选:A.
【点睛】考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行(或共线)且相等.
13.【考点】角的计算和垂线的定义
【分析】利用垂直的概念和互余的性质计算.
解:∵∠PQR等于138°,SQ⊥QR,
∴∠PQS=138°-90°=48°,
又∵QT⊥PQ,
∴∠PQT=90°,
∴∠SQT=42°.
故答案是42°.
【点睛】此题主要考查了角的计算和垂线的定义的知识,解题关键点是熟练掌握有公共部分的两个直角的计算.
14.【考点】平行线的性质
【分析】先根据AB∥CD得到∠BFD=∠B=32°,再根据角平分线的性质得到∠EFD=2∠BFD,再根据平行线的性质得到∠1=∠EFD即可.
解:∵AB∥CD
∴∠BFD=∠B=32°,
∵FB平分∠EFD
∴∠EFD=2∠BFD=64°,
∴∠1=∠EFD=64°.
【点睛】此题主要考查平行线的性质,解题的关键是熟知平行线的性质定理.
15.【考点】平行线的判定
【分析】根据平行线的判定方法去解答.
解:①∠1=∠3.∴DC∥AB;③∠A+∠3+∠4=180°,∴AD∥BC;正确的有②④.
故答案为:②④.
【点睛】此题重点考查学生对平行线的判定方法的理解,熟练掌握平行线的判定方法是解题的关键.
16.【考点】平行线的性质
【分析】根据两直线平行的性质去解答.
解:
故答案为:
【点睛】此题重点考察学生对两直线平行的性质的应用,熟练掌握两直线平行的性质是解题的关键.
17.【考点】平行线的性质
【分析】根据平行线的性质,利用角的和差关系直接作答即可.
解:∵AB∥DC,
∴∠DCO=∠B=76°.
∵AD∥BC,
∴∠ADC=∠DCO=76°.
又∵∠EDA=48°,
∴∠CDO=180°﹣∠EDA﹣∠ADC=56°.
故答案为:56.
【点睛】本题考查了平行线的性质,解决问题的关键是由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.
18.【考点】平移的性质
【分析】根据平移的性质得S△ABC=S△DEF,BE=6,DE=AB=10,则可计算出OE=DE-DO=6,再利用S阴影部分+S△OEC=S梯形ABEO+S△OEC得到S阴影部分=S梯形ABEO,然后根据梯形的面积公式求解.
解:∵△ABC沿着点B到C的方向平移到△DEF的位置,平移距离为6,
∴S△ABC=S△DEF,BE=6,DE=AB=10,
∴OE=DE-DO=6,
∵S阴影部分+S△OEC=S梯形ABEO+S△OEC,
∴S阴影部分=S梯形ABEO=×(6+10)×6=48.
故答案为:48.
【点睛】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.
19.【考点】平行线的性质与判定
【分析】根据平行线的性质与判定即可写出.
证明:∵∠1=∠2(已知),∠2=∠AGB(对顶角相等)
∴∠1=∠AGB
∴EC∥BF(同位角相等,两直线平行)
∴∠B=∠AEC(两直线平行,同位角相等)
又∵∠B=∠C(已知)
∴∠AEC= ∠C (等量替换)
∴AB∥CD(内错角相等,两直线平行)
∴∠A=∠D(两直线平行,内错角相等)
【点睛】此题主要考查平行线的性质与判定,解题的关键是熟知平行线判定的方法.
20.【考点】平行线的性质与判定
【分析】先由同位角相等,得出两直线平行,再根据两直线平行,得出内错角相等,最后根据同位角相等,得出两直线平行即可.
解:∵(已知)
∴(同位角相等,两直线平行)
又∵(两直线平行,内错角相等)
∴(等量代换)
∴(同位角相等,两直线平行)
【点睛】本题主要考查了平行线的判定与性质,解题时注意:两直线平行,内错角相等;同位角相等,两直线平行.
21.【考点】平移变换作图
【分析】(1)连接BB′,过A、C分别做BB′的平行线,并且在平行线上截取AA′=CC′=BB′,顺次连接平移后各点,得到的三角形即为平移后的三角形;
(2)作AB的垂直平分线找到中点D,连接CD,CD就是所求的中线.
(3)从A点向BC的延长线作垂线,垂足为点E,AE即为BC边上的高;
(4)根据三角形面积公式即可求出△A′B′C′的面积.
解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:CD就是所求的中线;
(3)如图所示:AE即为BC边上的高;
(4)S△A′B′C′=4×4÷2=16÷2=8.
故△A′B′C′的面积为8.
【点睛】考查了根据平移变换作图,其中平移作图的一般步骤为:①确定平移的方向和距离,先确定一组对应点;②确定图形中的关键点;③利用第一组对应点和平移的性质确定图中所有关键点的对应点;④按原图形顺序依次连接对应点,所得到的图形即为平移后的图形.同时考查了三角形的中线,高的一些基本画图方法.
22.【考点】邻补角,角平分线的定义
【分析】(1)根据角平分线的定义求出∠MOB的度数,根据邻补角的性质计算即可.
(2)根据题意得到:∠DOM为∠CON的邻补角.
解:(1)∵∠AOC+∠AOD=∠AOD+∠BOD=180°,
∴∠BOD=∠AOC=50°,
∵OM平分∠BOD,
∴∠BOM=∠DOM=25°,
又由∠MON=90°,
∴∠AON=180°-(∠MON+∠BOM)=180°-(90°+25°)=65°;
(2)∵∠AON=65°,∠AOC=50°,
∴∠CON=∠AON+∠AOC=115°,即∠DON的邻补角的度数为115°.
【点睛】本题考查的是邻补角的概念以及角平分线的定义,掌握邻补角的性质是邻补角互补是解题的关键.
23.【考点】平行线的性质和判定
【分析】(1)求出∠ABC+∠A=180°,根据平行线的判定推出即可;
(2)根据平行线的性质求出∠DBC,根据垂直推出BD∥EF,根据平行线的性质即可求出∠EFC.
(1)证明:∵∠ABC=180°-∠A,
∴∠ABC+∠A=180°,
∴AD∥BC;
(2)∵AD∥BC,∠ADB=36°,
∴∠DBC=∠ADB=36°,
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠DBC=∠EFC=36°
【点睛】本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.
24.【考点】平行线的性质
【分析】先由GM⊥GE得出∠EGM=90°,求出∠EGB =70°,利用对顶角得到∠AGH=70°,由AB∥CD得∠CHG=110°,由HN平分∠CHE得∠NHC=∠CHG=55°
再利用平角的性质即可求出∠NHD的度数.
解:∵GM⊥GE
∴∠EGM=90°
∵∠BGM=20°
∴∠EGB=∠EGM-∠BGM=70°
∴∠AGH=∠EGB=70°
∵AB∥CD
∴∠AGH+∠CHG=180°
∴∠CHG=110°
∵HN平分∠CHE
∴∠NHC=∠CHG=×110°=55°
∴∠NHD=180°-∠CHN=180°-55°=125°
【点睛】此题主要考查平行线的性质,解题的关键是熟知平行线的性质与垂直,平角的性质.
25.【考点】平行线的性质
【分析】(1)先根据平行线的性质得出∠BCD的度数,再由∠ABE=2∠ABC即可得出∠BCD的度数;
(2)先用x表示出∠ABE与∠BCE的度数,再根据三角形内角和定理求出x的值,进而可得出结论.
解:(1)∵CD∥AB,∠ABC=x°,
∴∠BCD=∠ABC=x°,∠D=∠ABE,
∵∠ABE=2∠ABC,
∴∠D=2∠ABC=2x°.
故答案为:x,2x;
(2)∵∠ABE=2∠ABC,∠BCE=4∠ABC,∠ABC=x°,
∴∠ABE=2x°,∠BCE=4x°.
在△BCE中,
∵∠ABE+∠ABC+∠BCE+∠E=180°,即2x+x+4x+40=180,解得x=20.
∴∠D=2x°=40°.
【点睛】本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等,内错角相等.
26.【考点】平行线的性质,角平分线的性质
【分析】(1)先根据平行线的性质,得出∠ABN=120°,再根据BC、BD分别平分∠ABP和∠PBN,即可得出∠CBD的度数;
(2)根据平行线的性质得出∠APB=∠PBN,∠ADB=∠DBN,再根据BD平分∠PBN,即可得到∠PBN=2∠DBN进而得出∠APB=2∠ADB;
(3)根据∠ACB=∠CBN,∠ACB=∠ABD,得出∠CBN=∠ABD,进而得到∠ABC=∠DBN,根据∠CBD=60°,∠ABN=120°,可求得∠ABC的度数.
解:(1),
,
,
,
平分,平分,
,
,
,
;
(2)不变,.
,
,,
平分,
,
;
(3),
,
当时,则有,
,
,
由(1)可知,,
,
.
【点睛】本题主要考查了平行线的性质,角平分线的性质的运用,解决问题的关键是掌握:两直线平行,内错角相等.
班级_____________考号______________姓名_______________总分_________________
一、选择题(12小题,每题3分,共36分)
1.如图各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
2.如图,直线AB和CD相交于O,那么图中 ∠DOE与∠COA 的关系是( )
A.对顶角 B.相等 C.互余 D.互补
3.如图,在△ABC中,∠C=90°,AC=4,点P是边BC上的动点,则AP的长不可能( )
A.3 B.4 C.5 D.6
4.下列说法正确的是( )
A.同旁内角互补
B.相等的角是对顶角
C.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
D.经过直线外一点,有且只有一条直线与已知直线平行
5.如图,已知直线AD、BE、CF相交于点O,OG⊥AD,且∠BOC=35°,∠FOG=30°,则∠DOE的度数为( )
A. B. C. D.
6.如图,下列条件中,不能判断直线的是( )
A. B. C. D.
7.一学员在广场上练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )
A.第一次向左拐30°,第二次向右拐30°
B.第一次向右拐50°,第二次向左拐130°
C.第一次向左拐50°,第二次向右拐130°
D.第一次向左拐50°,第二次向左拐130
8.如图,AB∥CD,直线EF分别交AB,CD于E,F,EG平分∠BEF.若∠1=72°,则∠2是( )度.
A.54 B.72 C.36 D.144.
9.如图,直线,,,则的度数是( )
A. B. C. D.
10.将一副三角板按如图的所示放置,下列结论中不正确的是( )
A.若,则有;
B.;
C.若,则有;
D.如果,必有.
11.如图,AB∥EF∥CD,点G在AB上,GE∥BC,GE的延长线交DC的延长线于点H,则图中与∠AGE相等的角共有( )
A.6个 B.5个 C.4个 D.3个
12.如图,在直角三角形ABC中,∠BAC=90°,AB=3,AC=4,将三角形ABC沿直线BC向右平移2.5个单位长度得到三角形DEF,连接AD,AE.有下列结论:①AC∥DF;②AD∥BE,AD=BE;③∠ABE=∠DEF;④ED⊥AC.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(6小题,每题3分,共18分)
13.如图,∠PQR=138°.SQ⊥QR于Q,QT⊥PQ于Q,则∠SQT等于______.
14.如图,AB∥CD,FB平分∠EFD,若∠B=32°,则∠1的度数是________.
15.如图,给出如下推理:①∠1=∠3.∴AD∥BC;②∠A+∠1+∠2=180°,∴AB∥CD;③∠A+∠3+∠4=180°,∴AB∥CD;④∠2=∠4,∴AD∥BC.其中正确的推理有_____.(填序号)
16.如图,直线 a∥b,直线 l 与 a,b 分别交于A、B 两点,过点B 作 BC⊥AB 交直线 a 于点 C,若∠1=65°,则∠2=_________
17.如图,已知,,点C在BO上,点E在OD的延长线上,若,,则的度数是______
18.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,,平移距离为6,则阴影部分面积为________.
三、解答题(8小题,共66分)
19.完成下面的证明过程:如图所示,直线AD与AB、CD分别相交于点A、D,与EC、BF分别相交于点H、G,已知∠1=∠2,∠B=∠C
求证:∠A=∠D
证明:∵∠1=∠2(已知),∠2=∠AGB( )
∴∠1=∠AGB
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC=_________( )
∴______________( )
∴∠A=∠D( )
20.如图,,,说明:.
21.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将经过一次平移后得到,图中标出了点B的对应点.
(1)在给定方格纸中画出平移后的;利用网格点和三角板画图或计算:
(2)画出边上的中线;
(3)画出边上的高线;
(4)的面积为 .
22.如图,AB、CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°.
(1)求∠AON的度数;
(2)求∠DON的邻补角的度数.
23.如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于E.
(1)求证:AD∥BC;
(2)若∠ADB=36°,求∠EFC的度数.
24.如图,AB∥CD,直线EF与AB,CD交于点G,H,GM⊥GE,∠BGM=20°,HN平分∠CHE,求∠NHD的度数.
25.如图,,,,,
(1)若设,则 °, °(用含的代数式表示);
(2)求的度数.
26.如图,已知,,点是射线上一动点(与点不重合),、分别平分和,分别交射线于点、.
(1)求的度数;
(2)当点运动时,与之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点运动到使时,求的度数.
参考答案
1.【考点】对顶角的定义
【分析】根据对顶角的定义判断即可.
解:根据两条直线相交,才能构成对顶角进行判断,
A、C、D都不是由两条直线相交构成的图形,错误,
B是由两条直线相交构成的图形,正确,
故选:B.
【点睛】本题主要考查了对顶角的定义,有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
2.【考点】垂线
【分析】先由垂直的定义得到∠AOE=∠BOE=90°,则∠DOE+∠BOD=90°,再根据对顶角相等得到∠BOD=∠AOC,所以∠DOE+∠AOC=90°,然后根据互余的定义进行判断.
解:∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∴∠DOE+∠BOD=90°,
∵∠BOD=∠AOC,
∴∠DOE+∠AOC=90°,
即∠DOE与∠COA互余.
故选:C.
【点睛】本题考查了垂线:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.垂线的性质过一点有且只有一条直线与已知直线垂直.也考查了对顶角和两角互余.
3.【考点】垂线段最短
【分析】根据垂线段最短分析即可.
解:已知,在△ABC中,∠C=90°,AC=4, 根据垂线段最短,可知AP的长不可小于4,当P和C重合时,AP=4, 故选:A.
【点睛】本题考查垂线段最短的性质,解题的关键是正确理解垂线段最短的性质.
4.【考点】平行线的性质,点到直线的距离,对顶角
【分析】依据平行线的性质、点到直线的距离以及对顶角的概念进行判断即可.
解:A、两直线平行,同旁内角才互补,故本选项错误;
B、相等的角位置关系不固定,对顶角是其中一种,故本选项错误;
C、距离是一段长度,用具体数值表示,从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离,故本选项错误;
D、经过直线外一点,有且只有一条直线与已知直线平行,故本选项正确.
故选:D.
【点睛】本题主要考查了平行线的性质、点到直线的距离以及对顶角的概念,解题时注意:点到直线的距离是一个长度,而不是一个图形,也就是垂线段的长度,而不是垂线段.
5.【考点】垂线,对顶角、邻补角
【分析】根据对顶角相等,以及垂直的定义求出所求角度数即可.
解:∵∠BOC=35°,∠FOG=30°,
∴∠EOF=∠BOC=35°,
∴∠GOE=∠GOF+∠FOE=65°,
∵OG⊥AD,
∴∠GOD=90°,
∴∠DOE=25°,
故选:D.
【点睛】此题考查了垂线,以及对顶角、邻补角,熟练掌握各自的性质是解本题的关键.
6.【考点】平行线的判定
【分析】根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行对各选项进行判断.
解:当∠1=∠3时,a∥b;
当∠4=∠5时,a∥b;
当∠2+∠4=180°时,a∥b.
故选:B.
【点睛】本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
7.【考点】平行线的判定
【分析】首先根据题意对各选项画出示意图,观察图形,根据同位角相等,两直线平行,即可得出答案.
解:如图:
故选A.
【点睛】此题考查了平行线的判定.注意数形结合法的应用,注意掌握同位角相等,两直线平行.
8.【考点】平行线的性质,角平分线的性质
【分析】根据两直线平行,同旁内角互补,内错角相等,可求出∠BEF=108°,∠2=∠BEG,然后再根据角平分线的性质可求出∠BEG,继而可求出∠2.
解:∵AB∥CD,
∴∠BEF=180°-∠1=180°-72°=108°,∠2=∠BEG,
又∵EG平分∠BEF,
∴∠2=∠BEG=∠BEF=×108°=54°,
故本题答案应为:A.
【点睛】平行线的性质和角平分线的性质是本题的考点,熟练掌握并正确运用其性质是解题的关键.
9.【考点】平行线性质
【分析】先根据平行线的性质,由l1∥l2得∠3=∠1=40°,再根据平行线的判定,由∠α=∠β得AB∥CD,然后根据平行线的性质得∠2+∠3=180°,再把∠1=40°代入计算即可.
解:如图,
∵l1∥l2,
∴∠3=∠1=40°,
∵∠α=∠β,
∴AB∥CD,
∴∠2+∠3=180°,
∴∠2=180°-∠3=180°-40°=140°.
故选:D.
【点睛】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.
10.【考点】平行线的判定与性质、余角和补角
【分析】根据两种三角板的各角的度数,利用平行线的判定与性质结合已知条件对各个结论逐一验证,即可得出答案.
解: ∵∠2=30°,
∴∠1=90°-30°=60°,
∵∠E=60°,
∴∠1=∠E,
∴AC∥DE.
∴A项正确;
∵∠1+∠2=90°,∠3+∠2=90°,
∴∠1+∠2+∠3+∠2=∠CAD+∠BAE=180°,
∴B项正确;
∵BC∥AD,
∴∠C+∠CAD=180°,
∵∠C=45°,
∴∠CAD =135°,
又∵∠CAD+∠BAE=180°,
∴∠2=∠BAE=180°-135°=45°,
∴C项错误;
∵∠CAD =150°,∠CAD+∠BAE=180°,
∴∠2=∠BAE=180°-150°=30°,
∴AC∥DE,
∴∠4=∠C,
∴D项正确;
故本题答案应为:C.
【点睛】此题主要考查了平行线的判定与性质、余角和补角的相关知识,熟练掌握两种三角板各角的度数是解题的关键.
11.【考点】平行线的性质
【分析】先由AB∥EF∥CD,根据两直线平行,内错角相等得到∠AGE=∠GEF,∠AGE=∠GHC;再由GE∥BC,根据平行线的性质,找出其它相等的角,注意做到不重不漏.
解:∵AB∥EF∥CD,
∴∠AGE=∠GEF,∠AGE=∠GHC.
∵GE∥BC,
∴∠AGE=∠ABP,∠GEF=∠BPF,∠GHC=∠BCD.
由对顶角相等,得∠BPF=∠EPC.
则与∠AGE相等的角有∠GEF,∠GHC,∠ABP,∠BPF,∠BCD,∠EPC共6个.
故选:A.
【点睛】本题考查平行线的性质,解题关键是熟练掌握:两直线平行,同位角相等,内错角相等.
12.【考点】平移的性质
【分析】根据平移的性质得到AC∥DF,AB∥DE,AD∥CF,AD=CF=2.5,∠EDF=∠BAC=90°,则利用平行线的性质得∠ABE=∠DEF,利用垂直的定义得DE⊥DF,于是根据平行线的性质可判断DE⊥AC.
解:∵将△ABC沿直线向右平移2.5个单位得到△DEF, ∴AC∥DF,AB∥DE,AD∥CF,AD=CF=2.5,∠EDF=∠BAC=90°, ∴∠ABE=∠DEF,DE⊥DF, ∴DE⊥AC, ∴①②③④都正确. 故选:A.
【点睛】考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行(或共线)且相等.
13.【考点】角的计算和垂线的定义
【分析】利用垂直的概念和互余的性质计算.
解:∵∠PQR等于138°,SQ⊥QR,
∴∠PQS=138°-90°=48°,
又∵QT⊥PQ,
∴∠PQT=90°,
∴∠SQT=42°.
故答案是42°.
【点睛】此题主要考查了角的计算和垂线的定义的知识,解题关键点是熟练掌握有公共部分的两个直角的计算.
14.【考点】平行线的性质
【分析】先根据AB∥CD得到∠BFD=∠B=32°,再根据角平分线的性质得到∠EFD=2∠BFD,再根据平行线的性质得到∠1=∠EFD即可.
解:∵AB∥CD
∴∠BFD=∠B=32°,
∵FB平分∠EFD
∴∠EFD=2∠BFD=64°,
∴∠1=∠EFD=64°.
【点睛】此题主要考查平行线的性质,解题的关键是熟知平行线的性质定理.
15.【考点】平行线的判定
【分析】根据平行线的判定方法去解答.
解:①∠1=∠3.∴DC∥AB;③∠A+∠3+∠4=180°,∴AD∥BC;正确的有②④.
故答案为:②④.
【点睛】此题重点考查学生对平行线的判定方法的理解,熟练掌握平行线的判定方法是解题的关键.
16.【考点】平行线的性质
【分析】根据两直线平行的性质去解答.
解:
故答案为:
【点睛】此题重点考察学生对两直线平行的性质的应用,熟练掌握两直线平行的性质是解题的关键.
17.【考点】平行线的性质
【分析】根据平行线的性质,利用角的和差关系直接作答即可.
解:∵AB∥DC,
∴∠DCO=∠B=76°.
∵AD∥BC,
∴∠ADC=∠DCO=76°.
又∵∠EDA=48°,
∴∠CDO=180°﹣∠EDA﹣∠ADC=56°.
故答案为:56.
【点睛】本题考查了平行线的性质,解决问题的关键是由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.
18.【考点】平移的性质
【分析】根据平移的性质得S△ABC=S△DEF,BE=6,DE=AB=10,则可计算出OE=DE-DO=6,再利用S阴影部分+S△OEC=S梯形ABEO+S△OEC得到S阴影部分=S梯形ABEO,然后根据梯形的面积公式求解.
解:∵△ABC沿着点B到C的方向平移到△DEF的位置,平移距离为6,
∴S△ABC=S△DEF,BE=6,DE=AB=10,
∴OE=DE-DO=6,
∵S阴影部分+S△OEC=S梯形ABEO+S△OEC,
∴S阴影部分=S梯形ABEO=×(6+10)×6=48.
故答案为:48.
【点睛】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.
19.【考点】平行线的性质与判定
【分析】根据平行线的性质与判定即可写出.
证明:∵∠1=∠2(已知),∠2=∠AGB(对顶角相等)
∴∠1=∠AGB
∴EC∥BF(同位角相等,两直线平行)
∴∠B=∠AEC(两直线平行,同位角相等)
又∵∠B=∠C(已知)
∴∠AEC= ∠C (等量替换)
∴AB∥CD(内错角相等,两直线平行)
∴∠A=∠D(两直线平行,内错角相等)
【点睛】此题主要考查平行线的性质与判定,解题的关键是熟知平行线判定的方法.
20.【考点】平行线的性质与判定
【分析】先由同位角相等,得出两直线平行,再根据两直线平行,得出内错角相等,最后根据同位角相等,得出两直线平行即可.
解:∵(已知)
∴(同位角相等,两直线平行)
又∵(两直线平行,内错角相等)
∴(等量代换)
∴(同位角相等,两直线平行)
【点睛】本题主要考查了平行线的判定与性质,解题时注意:两直线平行,内错角相等;同位角相等,两直线平行.
21.【考点】平移变换作图
【分析】(1)连接BB′,过A、C分别做BB′的平行线,并且在平行线上截取AA′=CC′=BB′,顺次连接平移后各点,得到的三角形即为平移后的三角形;
(2)作AB的垂直平分线找到中点D,连接CD,CD就是所求的中线.
(3)从A点向BC的延长线作垂线,垂足为点E,AE即为BC边上的高;
(4)根据三角形面积公式即可求出△A′B′C′的面积.
解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:CD就是所求的中线;
(3)如图所示:AE即为BC边上的高;
(4)S△A′B′C′=4×4÷2=16÷2=8.
故△A′B′C′的面积为8.
【点睛】考查了根据平移变换作图,其中平移作图的一般步骤为:①确定平移的方向和距离,先确定一组对应点;②确定图形中的关键点;③利用第一组对应点和平移的性质确定图中所有关键点的对应点;④按原图形顺序依次连接对应点,所得到的图形即为平移后的图形.同时考查了三角形的中线,高的一些基本画图方法.
22.【考点】邻补角,角平分线的定义
【分析】(1)根据角平分线的定义求出∠MOB的度数,根据邻补角的性质计算即可.
(2)根据题意得到:∠DOM为∠CON的邻补角.
解:(1)∵∠AOC+∠AOD=∠AOD+∠BOD=180°,
∴∠BOD=∠AOC=50°,
∵OM平分∠BOD,
∴∠BOM=∠DOM=25°,
又由∠MON=90°,
∴∠AON=180°-(∠MON+∠BOM)=180°-(90°+25°)=65°;
(2)∵∠AON=65°,∠AOC=50°,
∴∠CON=∠AON+∠AOC=115°,即∠DON的邻补角的度数为115°.
【点睛】本题考查的是邻补角的概念以及角平分线的定义,掌握邻补角的性质是邻补角互补是解题的关键.
23.【考点】平行线的性质和判定
【分析】(1)求出∠ABC+∠A=180°,根据平行线的判定推出即可;
(2)根据平行线的性质求出∠DBC,根据垂直推出BD∥EF,根据平行线的性质即可求出∠EFC.
(1)证明:∵∠ABC=180°-∠A,
∴∠ABC+∠A=180°,
∴AD∥BC;
(2)∵AD∥BC,∠ADB=36°,
∴∠DBC=∠ADB=36°,
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠DBC=∠EFC=36°
【点睛】本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.
24.【考点】平行线的性质
【分析】先由GM⊥GE得出∠EGM=90°,求出∠EGB =70°,利用对顶角得到∠AGH=70°,由AB∥CD得∠CHG=110°,由HN平分∠CHE得∠NHC=∠CHG=55°
再利用平角的性质即可求出∠NHD的度数.
解:∵GM⊥GE
∴∠EGM=90°
∵∠BGM=20°
∴∠EGB=∠EGM-∠BGM=70°
∴∠AGH=∠EGB=70°
∵AB∥CD
∴∠AGH+∠CHG=180°
∴∠CHG=110°
∵HN平分∠CHE
∴∠NHC=∠CHG=×110°=55°
∴∠NHD=180°-∠CHN=180°-55°=125°
【点睛】此题主要考查平行线的性质,解题的关键是熟知平行线的性质与垂直,平角的性质.
25.【考点】平行线的性质
【分析】(1)先根据平行线的性质得出∠BCD的度数,再由∠ABE=2∠ABC即可得出∠BCD的度数;
(2)先用x表示出∠ABE与∠BCE的度数,再根据三角形内角和定理求出x的值,进而可得出结论.
解:(1)∵CD∥AB,∠ABC=x°,
∴∠BCD=∠ABC=x°,∠D=∠ABE,
∵∠ABE=2∠ABC,
∴∠D=2∠ABC=2x°.
故答案为:x,2x;
(2)∵∠ABE=2∠ABC,∠BCE=4∠ABC,∠ABC=x°,
∴∠ABE=2x°,∠BCE=4x°.
在△BCE中,
∵∠ABE+∠ABC+∠BCE+∠E=180°,即2x+x+4x+40=180,解得x=20.
∴∠D=2x°=40°.
【点睛】本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等,内错角相等.
26.【考点】平行线的性质,角平分线的性质
【分析】(1)先根据平行线的性质,得出∠ABN=120°,再根据BC、BD分别平分∠ABP和∠PBN,即可得出∠CBD的度数;
(2)根据平行线的性质得出∠APB=∠PBN,∠ADB=∠DBN,再根据BD平分∠PBN,即可得到∠PBN=2∠DBN进而得出∠APB=2∠ADB;
(3)根据∠ACB=∠CBN,∠ACB=∠ABD,得出∠CBN=∠ABD,进而得到∠ABC=∠DBN,根据∠CBD=60°,∠ABN=120°,可求得∠ABC的度数.
解:(1),
,
,
,
平分,平分,
,
,
,
;
(2)不变,.
,
,,
平分,
,
;
(3),
,
当时,则有,
,
,
由(1)可知,,
,
.
【点睛】本题主要考查了平行线的性质,角平分线的性质的运用,解决问题的关键是掌握:两直线平行,内错角相等.
