沪科版八年级下册数学 17.5 一元二次方程的应用 课件 共54张PPT
文档属性
| 名称 | 沪科版八年级下册数学 17.5 一元二次方程的应用 课件 共54张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-13 12:25:59 | ||
图片预览






文档简介
课件54张PPT。17.5 一元二次方程的应用几何与方程5xx xx (8-2x)(5-2x)8
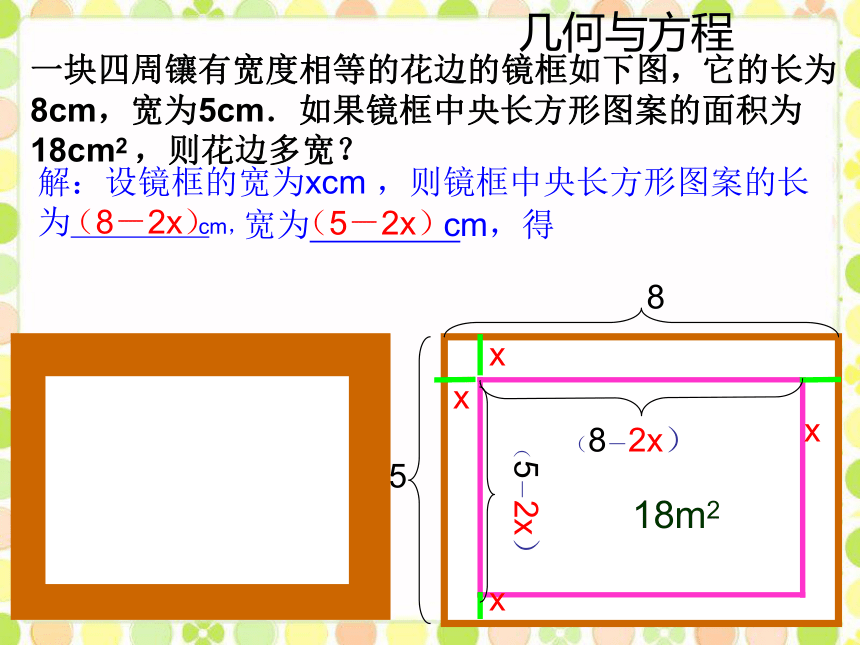
一块四周镶有宽度相等的花边的镜框如下图,它的长为8cm,宽为5cm.如果镜框中央长方形图案的面积为18cm2 ,则花边多宽?解:设镜框的宽为xcm ,则镜框中央长方形图案的长为 cm,
宽为 cm,得 (8-2x)(5-2x)18m2解:设镜框的宽为xcm ,则镜框中央长方形
图案的长为 cm,
宽为 cm,得(8 - 2x) (5 - 2x) = 18 (8-2x)(5-2x)即2X2 - 13 X + 11=0解得X1=1,
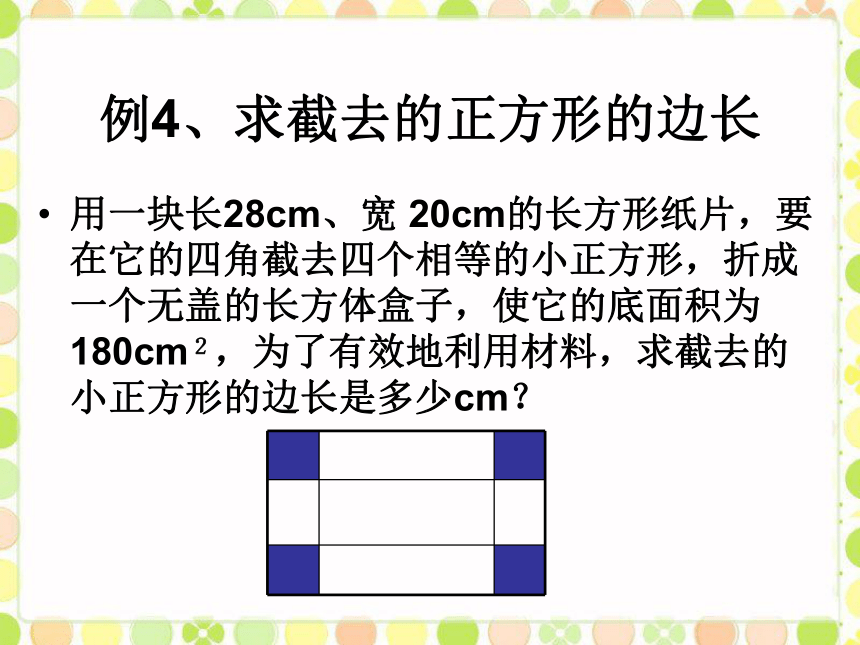
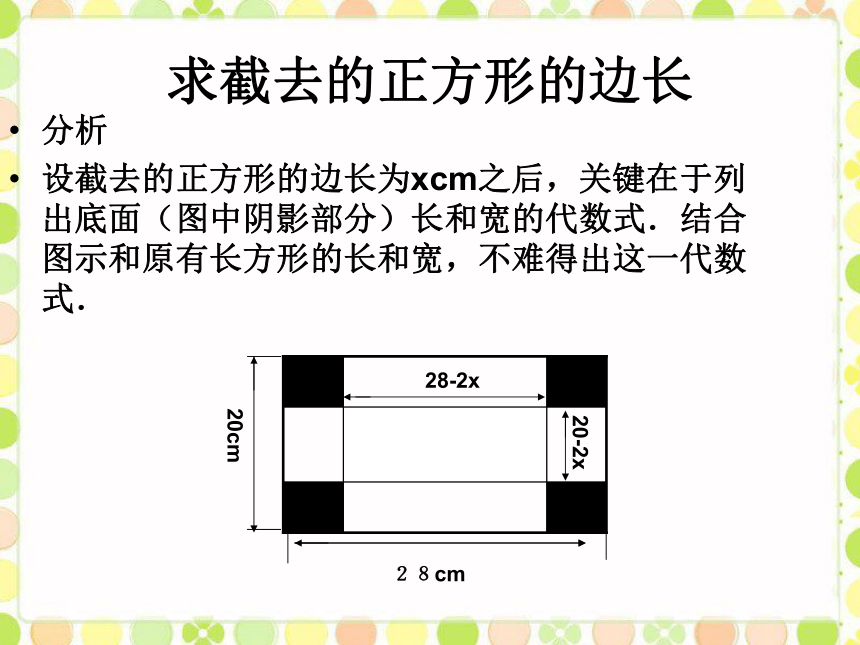
X2=5.5(不合题意)答:镜框的宽为1m.审设答解列4、建造一个池底为正方形,深度为2.5m的长方体无盖蓄水池,建造池壁的单价是120元/m2,建造池底的单价是240元/m2,总造价是8640元,求池底的边长.分析:池底的造价+池壁的造价=总造价解:设池底的边长是xm.根据题意得:解方程得:∵池底的边长不能为负数,∴取x=4答:池底的边长是4m.小结:解决这类问题的关键是掌握常见几何图形的面积体积公式,并能熟练计算由基本图形构成的组合图形的面积.例2:如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长. 答:截去正方形的边长为10厘米. 例4、求截去的正方形的边长用一块长28cm、宽 20cm的长方形纸片,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体盒子,使它的底面积为180cm2,为了有效地利用材料,求截去的小正方形的边长是多少cm?求截去的正方形的边长分析
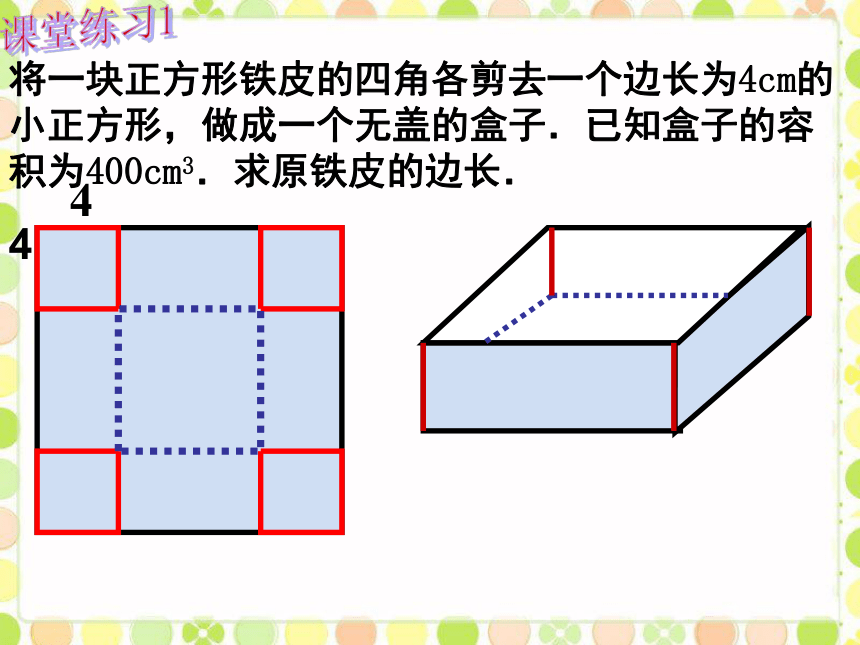
设截去的正方形的边长为xcm之后,关键在于列出底面(图中阴影部分)长和宽的代数式.结合图示和原有长方形的长和宽,不难得出这一代数式.将一块正方形铁皮的四角各剪去一个边长为4cm的小正方形,做成一个无盖的盒子.已知盒子的容积为400cm3.求原铁皮的边长. 课堂练习1 4 4有一块面积为75米2的长方形鸡场,它的一边靠墙(墙长18米)另三边用 木栏围成,如果 木栏长35
米,鸡场的长与宽各是多少?18m(1)题目中哪些话体现了等量关系?
(2)你能用等式描述这些等量关系吗?
(3)设墙所对的木栏长为x米,
鸡场的宽是 ,
(4)列出方程,只列不解. (5)此方程的解为30或5,你怎么处理?为什么?x列一元二次方程解应题补充练习:(98年北京市崇文区中考题)如图,有一面
积是150平方米的长方形鸡场,鸡场的一边靠墙
(墙长18米),墙对面有一个2米宽的门,另三边
(门除外)用竹篱笆围成,篱笆总长33米.求鸡
场的长和宽各多少米?我是最棒的设计师 在一块长16m,宽12m的长方形土地上,要建造一个花园,使花园所占面积为长方形面积的一半. 你能设计出美观的图案吗?方案一:如图所示,花园四周小路的宽都相等.小路的宽是多少?(2)方程的解为2或12,因此,小路的宽为2m或12m.这样对吗?为什么?
在一块长16m,宽12m的长方形土地上,要建造一个花园,使花园所占面积为长方形面积的一半.(1)设小路的宽为xm,你能列出方程吗?方案二:如图所示.花园每个角上的扇形都相同,
你能通过解方程,得到扇形的半径x是多少吗?
(1)请列出方程. (2)方程的根为5.5或-5.5,
你怎么处理?1612x方案三:如图所示. 花园互相垂直,并且它的
宽都相等.你能通过解方程得到花园宽是多少
吗?如图,要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形.如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(精确到0.1cm)?分析:封面的长宽之比为_____________,中央的长方形的长宽之比也应是_____,由此判断上下边衬与左右边衬的宽度之比也是_____.
设上、下边衬的宽均为9x cm,左、右边衬的宽均为7x cm,则中央矩形的长为 (27-18x)cm,宽__________cm.
要使四周的彩色边衬所占面积是封面面积的四分之一,则中央矩形的面积是封面面积的四分之三.27:21=9:79:7(21-14x)9:7整理,得解方程,得上、下边衬的宽均为_____cm,
左、右边衬的宽均为_____cm.方程的哪个根合乎实际意义?为什么?1.81.4x2更合乎实际意义,如果取x1约等于2.799,那么上边衬宽为9×2.799=25.191,不合实际.于是可列出方程有关面积问题:常见的图形有下列几种:例2、用22cm长的铁丝,折成一个面积为30cm2的矩形.求这个矩形的长与宽.整理后,得x2-11x+30=0
解这个方程,得x1=5,x2=6(与题设不符,舍去)答:这个矩形的长是6cm,宽是5cm.解:设这个矩形的长为xcm,则宽为 (cm).
根据题意,得则横向的路面面积为 ,在长32米,宽20米的矩形空地上修两条等宽且互相垂直的小路,余下的耕地面积等于540米2.求小路的宽?解法一:
如图,设道路的宽为x米,32x 米2纵向的路面面积为 .20x 米2注意:这两个面积的重叠部分是 x2 米2其中的 x=50超出了原矩形的长和宽,应舍去.
取x=2时,道路总面积为:答:所求道路的宽为2米.解法二:
我们利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路)数字与方程例5:一个两位数,它的十位数字比个位数字小3,而它的个位数字的平方恰好等于这个两位数.求这个两位数.数字与方程3.有一个两位数,它的十位数字与个位数字的和是5.把这个两位数的十位数字与个位数字互换后得到另一个两位数,两个两位数的积为736.求原来的两位数.数字与方程5、两个数的差等于4,积等于45,求这两个数. 增长率与方程:二中小明学习非常认真,学习成绩直线
上升,第一次月考数学成绩是a分,第二次月考增长了10%,
第三次月考又增长了10%,问他第三次数学成绩是多少?分析:第三次第二次第一次aaX10%a+aX10%=a(1+10%)X10%a(1+10%)+ a(1+10%) X10% =a(1+10%)2a(1+10%)3、某电冰箱厂每个月的产量都比上个月增长的百分数相同.已知该厂今年4月份的电冰箱产量为5万台,6月份比5月份多生产了12000台,求该厂今年产量的月平均增长率为多少?增长率与方程?1、市第四中学初三年级初一开学时就参加课程改革试验,重视学生能力培养.初一阶段就有48人在市级以上各项活动中得奖,之后逐年增加,到三年级结束共有183人次在市级以上得奖.求这两年中得奖人次的平均年增长率.
1.甲公司前年缴税40万元,今年缴税48.4万元.该公司缴税的年平均增长率为多少?增长率与方程课前热身2:某经济开发区今年一月份工业产值达50亿元,三月份产值为72亿元,问二月、三月平均每月的增长率是多少? 解:设平均每月增长的百分率为 x,
根据题意得方程为50(1+x)2=72 可化为:解得:答:二月、三月平均每月的增长率是20%例1、平阳按“九五”国民经济发展规划要求,2003年的社会总产值要比2001年增长21%,求平均每年增长的百分率.(提示:基数为2001年的社会总产值,可视为a)设每年增长率为x,2001年的总产值为a,则2001年
a2002年
a(1+x)2003年
a(1+x) 2a(1+x) 2 =a+21%a分析:a (1+x) 2 =1.21 a
(1+x) 2 =1.21
1+x =1.1
x =0.1解:设每年增长率为x,2001年的总产值为a,则a(1+x) 2 =a+21%a答:平均每年增长的百分率为10% .2.某公司计划经过两年把某种商品的生产成本降低19%,那么平均每年需降低百分之几?增长率与方程 两年前生产 1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产 1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,哪种药品成本的年平均下降率较大? 分析:甲种药品成本的年平均下降额为
(5000-3000)÷2=1000(元)
乙种药品成本的年平均下降额为
(6000-3600)÷2=1200(元)
乙种药品成本的年平均下降额较大.但是,年平均下降额(元)不等同于年平均下降率(百分数).
解方程,得答:甲种药品成本的年平均下降率约为22.5%.解:设甲种药品成本的年平均下降率为x,则一年后甲种药品成本为 元,两年后甲种药品成本为 元,于是有根据问题的实际意义,成本的年下降率应是小于1的正数,所以应选取0.225.算一算:
乙种药品成本的年平均下降率是多少?比较:两种药品成本的年平均下降率.相同,都是22.5 %.设乙种药品的下降率为y.解方程,得答:甲种药品成本的年平均下降率约为22.5%.销售问题4.某商场销售一批名牌衬衫,现在平均每天能售出20件,每件盈利40元.为了尽快减少库存,商场决定采取降价措施.经调查发现:如果这种衬衫的售价每降低1元时,平均每天能多售出2件.商场要想平均每天盈利1200元,每件衬衫应降价多少元?源于生活,服务于生活5.某商店从厂家以每件21元的价格购进一批商品,若每件商品售价为x元,则每天可卖出(350-10x)件,但物价局限定每件商品加价不能超过进价的20%.商店要想每天赚400元,需要卖出多少件商
品?每件商品的售价应为多少元?销售问题6、某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量.试验发现,每多种一棵桃树,每棵棵桃树的产量就会减少2个.如果要使产量增加15.2%,那么应种多少棵桃树?经济效益与方程有关“动点”的运动问题”1)关键—— 以静代动
把动的点进行转换,变为线段的长度, 2)方法—— 时间变路程
求“动点的运动时间”可以转化为求“动点的运动路程”,也是求线段的长度;由此,学会把动点的问题转化为静点的问题,
是解这类问题的关键.3)常找的数量关系——
面积,勾股定理等;例1: 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B同时出发,几秒后⊿ PBQ的面积等于8cm2?例2:等腰直角⊿ ABC中,AB=BC=8cm,动点P从A点出发,沿AB向B移动,通过点P引平行于BC,AC的直线与AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm2?练习2:在直角三角形ABC中,AB=BC=12cm,点D从点A开始以2cm/s的速度沿AB边向点B移动,过点D做DE平行于BC,DF平行于AC,点E.F分别在AC,BC上,问:点D出发几秒后四边形DFCE的面积为20cm2?练习1: 在△ABC中, AC=50cm, CB=40cm, ∠C=90°,点P从点A开始沿AC边向点C以2cm/s的速度移动, 同时另一点Q由C点以3cm/s的速度沿着CB边移动,几秒钟后,△PCQ的面积等于450cm2?QBACP6. 某汽车在公路上行驶,它的路程s(m)和时间t(s)之间的关系为:s=10t+3t2,那么行驶 200m需要多长时间?运动与方程8、小明将勤工助学挣得的500元钱按一年定期存入银行,到期后取出50元用来购买学习用品 剩下的450元连同应得的税后利息又全部按一年定期存入银行如果存款的年利率保持不变,且到期后可得税后本息约461元,那么这种存款的年利率大约是多少? (精确到0.01%) .美满生活与方程??9、小红的妈妈前年存了5000元一年期的定期储蓄,到期后自动转存.今年到期扣除利息税(利息税为利息的20%),共取得5145元.求这种储蓄的年利率.(精确到0.1%)
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?开始有一人患了流感,第一轮的传染源就是这个人,他传染了x个人,用代数式表示,第一轮后共有_____人患了流感;第二轮传染中,这些人中的每个人又传染了x个人,用代数式表示,第二轮后共有_________人患了流感.1+x1+x+x(1+x)1+x+x(1+x)=121.解方程,得答:平均一个人传染了_____个人.10-12(不合题意,舍去)10列方程如果按照这样的传染速度,
三轮传染后有多少人患流感?121+121×10=1331人1.(P58-6)要组织一场篮球联赛,赛制为单循环形式,即每两队之间都赛一场,计划安排15场比赛,应邀请多少个球队参加比赛?2.要组织一场篮球联赛, 每两队之间都赛2场,计划安排90场比赛,应邀请多少个球队参加比赛?3.(P34-7)参加一次聚会的每两人都握了一次手,所有人共握手10次,有多少人参加聚会?4.一次会议上,每两个参加会议的人都互相握了一次手,有人统计一共握了66次手.这次会议到会的人数是多少?美满生活与方程典型练习题1、一个两位数个位数字比十位数字大1,个位数字与十位数字对调后所得的两位数比原数大9,求:这个两位数
2、一件商品原价200元经过两次降价后162元,求:平均降价的百分比
3、某班同学在圣诞节期间互赠礼物182件,求:这个班级的人数
4、某校进行乒乓球单循环比赛,共比赛55场,问:共有多少名同学参加
5、 一名同学进行登山训练,上山速度为2千米/小时,下山速度为6千米/小时,求:往返一次的平均速度
一块四周镶有宽度相等的花边的镜框如下图,它的长为8cm,宽为5cm.如果镜框中央长方形图案的面积为18cm2 ,则花边多宽?解:设镜框的宽为xcm ,则镜框中央长方形图案的长为 cm,
宽为 cm,得 (8-2x)(5-2x)18m2解:设镜框的宽为xcm ,则镜框中央长方形
图案的长为 cm,
宽为 cm,得(8 - 2x) (5 - 2x) = 18 (8-2x)(5-2x)即2X2 - 13 X + 11=0解得X1=1,
X2=5.5(不合题意)答:镜框的宽为1m.审设答解列4、建造一个池底为正方形,深度为2.5m的长方体无盖蓄水池,建造池壁的单价是120元/m2,建造池底的单价是240元/m2,总造价是8640元,求池底的边长.分析:池底的造价+池壁的造价=总造价解:设池底的边长是xm.根据题意得:解方程得:∵池底的边长不能为负数,∴取x=4答:池底的边长是4m.小结:解决这类问题的关键是掌握常见几何图形的面积体积公式,并能熟练计算由基本图形构成的组合图形的面积.例2:如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长. 答:截去正方形的边长为10厘米. 例4、求截去的正方形的边长用一块长28cm、宽 20cm的长方形纸片,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体盒子,使它的底面积为180cm2,为了有效地利用材料,求截去的小正方形的边长是多少cm?求截去的正方形的边长分析
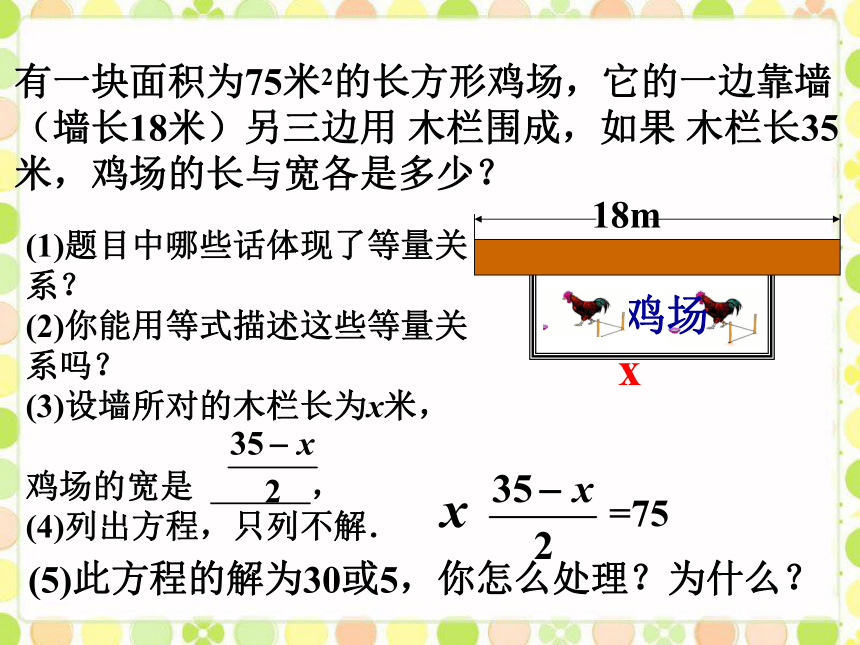
设截去的正方形的边长为xcm之后,关键在于列出底面(图中阴影部分)长和宽的代数式.结合图示和原有长方形的长和宽,不难得出这一代数式.将一块正方形铁皮的四角各剪去一个边长为4cm的小正方形,做成一个无盖的盒子.已知盒子的容积为400cm3.求原铁皮的边长. 课堂练习1 4 4有一块面积为75米2的长方形鸡场,它的一边靠墙(墙长18米)另三边用 木栏围成,如果 木栏长35
米,鸡场的长与宽各是多少?18m(1)题目中哪些话体现了等量关系?
(2)你能用等式描述这些等量关系吗?
(3)设墙所对的木栏长为x米,
鸡场的宽是 ,
(4)列出方程,只列不解. (5)此方程的解为30或5,你怎么处理?为什么?x列一元二次方程解应题补充练习:(98年北京市崇文区中考题)如图,有一面
积是150平方米的长方形鸡场,鸡场的一边靠墙
(墙长18米),墙对面有一个2米宽的门,另三边
(门除外)用竹篱笆围成,篱笆总长33米.求鸡
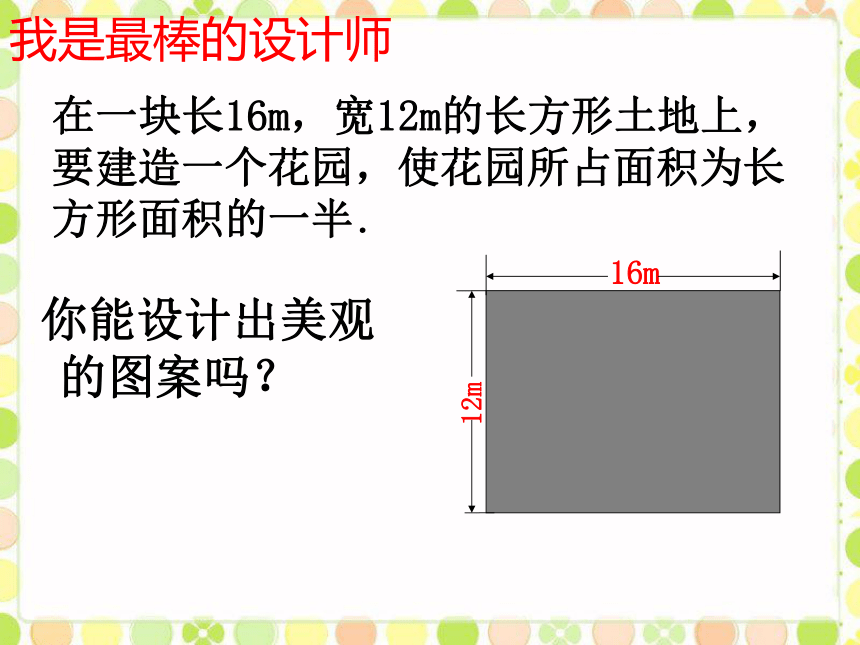
场的长和宽各多少米?我是最棒的设计师 在一块长16m,宽12m的长方形土地上,要建造一个花园,使花园所占面积为长方形面积的一半. 你能设计出美观的图案吗?方案一:如图所示,花园四周小路的宽都相等.小路的宽是多少?(2)方程的解为2或12,因此,小路的宽为2m或12m.这样对吗?为什么?
在一块长16m,宽12m的长方形土地上,要建造一个花园,使花园所占面积为长方形面积的一半.(1)设小路的宽为xm,你能列出方程吗?方案二:如图所示.花园每个角上的扇形都相同,
你能通过解方程,得到扇形的半径x是多少吗?
(1)请列出方程. (2)方程的根为5.5或-5.5,
你怎么处理?1612x方案三:如图所示. 花园互相垂直,并且它的
宽都相等.你能通过解方程得到花园宽是多少
吗?如图,要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形.如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(精确到0.1cm)?分析:封面的长宽之比为_____________,中央的长方形的长宽之比也应是_____,由此判断上下边衬与左右边衬的宽度之比也是_____.
设上、下边衬的宽均为9x cm,左、右边衬的宽均为7x cm,则中央矩形的长为 (27-18x)cm,宽__________cm.
要使四周的彩色边衬所占面积是封面面积的四分之一,则中央矩形的面积是封面面积的四分之三.27:21=9:79:7(21-14x)9:7整理,得解方程,得上、下边衬的宽均为_____cm,
左、右边衬的宽均为_____cm.方程的哪个根合乎实际意义?为什么?1.81.4x2更合乎实际意义,如果取x1约等于2.799,那么上边衬宽为9×2.799=25.191,不合实际.于是可列出方程有关面积问题:常见的图形有下列几种:例2、用22cm长的铁丝,折成一个面积为30cm2的矩形.求这个矩形的长与宽.整理后,得x2-11x+30=0
解这个方程,得x1=5,x2=6(与题设不符,舍去)答:这个矩形的长是6cm,宽是5cm.解:设这个矩形的长为xcm,则宽为 (cm).
根据题意,得则横向的路面面积为 ,在长32米,宽20米的矩形空地上修两条等宽且互相垂直的小路,余下的耕地面积等于540米2.求小路的宽?解法一:
如图,设道路的宽为x米,32x 米2纵向的路面面积为 .20x 米2注意:这两个面积的重叠部分是 x2 米2其中的 x=50超出了原矩形的长和宽,应舍去.
取x=2时,道路总面积为:答:所求道路的宽为2米.解法二:
我们利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路)数字与方程例5:一个两位数,它的十位数字比个位数字小3,而它的个位数字的平方恰好等于这个两位数.求这个两位数.数字与方程3.有一个两位数,它的十位数字与个位数字的和是5.把这个两位数的十位数字与个位数字互换后得到另一个两位数,两个两位数的积为736.求原来的两位数.数字与方程5、两个数的差等于4,积等于45,求这两个数. 增长率与方程:二中小明学习非常认真,学习成绩直线
上升,第一次月考数学成绩是a分,第二次月考增长了10%,
第三次月考又增长了10%,问他第三次数学成绩是多少?分析:第三次第二次第一次aaX10%a+aX10%=a(1+10%)X10%a(1+10%)+ a(1+10%) X10% =a(1+10%)2a(1+10%)3、某电冰箱厂每个月的产量都比上个月增长的百分数相同.已知该厂今年4月份的电冰箱产量为5万台,6月份比5月份多生产了12000台,求该厂今年产量的月平均增长率为多少?增长率与方程?1、市第四中学初三年级初一开学时就参加课程改革试验,重视学生能力培养.初一阶段就有48人在市级以上各项活动中得奖,之后逐年增加,到三年级结束共有183人次在市级以上得奖.求这两年中得奖人次的平均年增长率.
1.甲公司前年缴税40万元,今年缴税48.4万元.该公司缴税的年平均增长率为多少?增长率与方程课前热身2:某经济开发区今年一月份工业产值达50亿元,三月份产值为72亿元,问二月、三月平均每月的增长率是多少? 解:设平均每月增长的百分率为 x,
根据题意得方程为50(1+x)2=72 可化为:解得:答:二月、三月平均每月的增长率是20%例1、平阳按“九五”国民经济发展规划要求,2003年的社会总产值要比2001年增长21%,求平均每年增长的百分率.(提示:基数为2001年的社会总产值,可视为a)设每年增长率为x,2001年的总产值为a,则2001年
a2002年
a(1+x)2003年
a(1+x) 2a(1+x) 2 =a+21%a分析:a (1+x) 2 =1.21 a
(1+x) 2 =1.21
1+x =1.1
x =0.1解:设每年增长率为x,2001年的总产值为a,则a(1+x) 2 =a+21%a答:平均每年增长的百分率为10% .2.某公司计划经过两年把某种商品的生产成本降低19%,那么平均每年需降低百分之几?增长率与方程 两年前生产 1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产 1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,哪种药品成本的年平均下降率较大? 分析:甲种药品成本的年平均下降额为
(5000-3000)÷2=1000(元)
乙种药品成本的年平均下降额为
(6000-3600)÷2=1200(元)
乙种药品成本的年平均下降额较大.但是,年平均下降额(元)不等同于年平均下降率(百分数).
解方程,得答:甲种药品成本的年平均下降率约为22.5%.解:设甲种药品成本的年平均下降率为x,则一年后甲种药品成本为 元,两年后甲种药品成本为 元,于是有根据问题的实际意义,成本的年下降率应是小于1的正数,所以应选取0.225.算一算:
乙种药品成本的年平均下降率是多少?比较:两种药品成本的年平均下降率.相同,都是22.5 %.设乙种药品的下降率为y.解方程,得答:甲种药品成本的年平均下降率约为22.5%.销售问题4.某商场销售一批名牌衬衫,现在平均每天能售出20件,每件盈利40元.为了尽快减少库存,商场决定采取降价措施.经调查发现:如果这种衬衫的售价每降低1元时,平均每天能多售出2件.商场要想平均每天盈利1200元,每件衬衫应降价多少元?源于生活,服务于生活5.某商店从厂家以每件21元的价格购进一批商品,若每件商品售价为x元,则每天可卖出(350-10x)件,但物价局限定每件商品加价不能超过进价的20%.商店要想每天赚400元,需要卖出多少件商
品?每件商品的售价应为多少元?销售问题6、某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量.试验发现,每多种一棵桃树,每棵棵桃树的产量就会减少2个.如果要使产量增加15.2%,那么应种多少棵桃树?经济效益与方程有关“动点”的运动问题”1)关键—— 以静代动
把动的点进行转换,变为线段的长度, 2)方法—— 时间变路程
求“动点的运动时间”可以转化为求“动点的运动路程”,也是求线段的长度;由此,学会把动点的问题转化为静点的问题,
是解这类问题的关键.3)常找的数量关系——
面积,勾股定理等;例1: 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B同时出发,几秒后⊿ PBQ的面积等于8cm2?例2:等腰直角⊿ ABC中,AB=BC=8cm,动点P从A点出发,沿AB向B移动,通过点P引平行于BC,AC的直线与AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm2?练习2:在直角三角形ABC中,AB=BC=12cm,点D从点A开始以2cm/s的速度沿AB边向点B移动,过点D做DE平行于BC,DF平行于AC,点E.F分别在AC,BC上,问:点D出发几秒后四边形DFCE的面积为20cm2?练习1: 在△ABC中, AC=50cm, CB=40cm, ∠C=90°,点P从点A开始沿AC边向点C以2cm/s的速度移动, 同时另一点Q由C点以3cm/s的速度沿着CB边移动,几秒钟后,△PCQ的面积等于450cm2?QBACP6. 某汽车在公路上行驶,它的路程s(m)和时间t(s)之间的关系为:s=10t+3t2,那么行驶 200m需要多长时间?运动与方程8、小明将勤工助学挣得的500元钱按一年定期存入银行,到期后取出50元用来购买学习用品 剩下的450元连同应得的税后利息又全部按一年定期存入银行如果存款的年利率保持不变,且到期后可得税后本息约461元,那么这种存款的年利率大约是多少? (精确到0.01%) .美满生活与方程??9、小红的妈妈前年存了5000元一年期的定期储蓄,到期后自动转存.今年到期扣除利息税(利息税为利息的20%),共取得5145元.求这种储蓄的年利率.(精确到0.1%)
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?开始有一人患了流感,第一轮的传染源就是这个人,他传染了x个人,用代数式表示,第一轮后共有_____人患了流感;第二轮传染中,这些人中的每个人又传染了x个人,用代数式表示,第二轮后共有_________人患了流感.1+x1+x+x(1+x)1+x+x(1+x)=121.解方程,得答:平均一个人传染了_____个人.10-12(不合题意,舍去)10列方程如果按照这样的传染速度,
三轮传染后有多少人患流感?121+121×10=1331人1.(P58-6)要组织一场篮球联赛,赛制为单循环形式,即每两队之间都赛一场,计划安排15场比赛,应邀请多少个球队参加比赛?2.要组织一场篮球联赛, 每两队之间都赛2场,计划安排90场比赛,应邀请多少个球队参加比赛?3.(P34-7)参加一次聚会的每两人都握了一次手,所有人共握手10次,有多少人参加聚会?4.一次会议上,每两个参加会议的人都互相握了一次手,有人统计一共握了66次手.这次会议到会的人数是多少?美满生活与方程典型练习题1、一个两位数个位数字比十位数字大1,个位数字与十位数字对调后所得的两位数比原数大9,求:这个两位数
2、一件商品原价200元经过两次降价后162元,求:平均降价的百分比
3、某班同学在圣诞节期间互赠礼物182件,求:这个班级的人数
4、某校进行乒乓球单循环比赛,共比赛55场,问:共有多少名同学参加
5、 一名同学进行登山训练,上山速度为2千米/小时,下山速度为6千米/小时,求:往返一次的平均速度
