沪科版八年级下册数学 17.4 一元二次方程的根与系数的关系 课件 共28张PPT
文档属性
| 名称 | 沪科版八年级下册数学 17.4 一元二次方程的根与系数的关系 课件 共28张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 285.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-13 17:08:38 | ||
图片预览


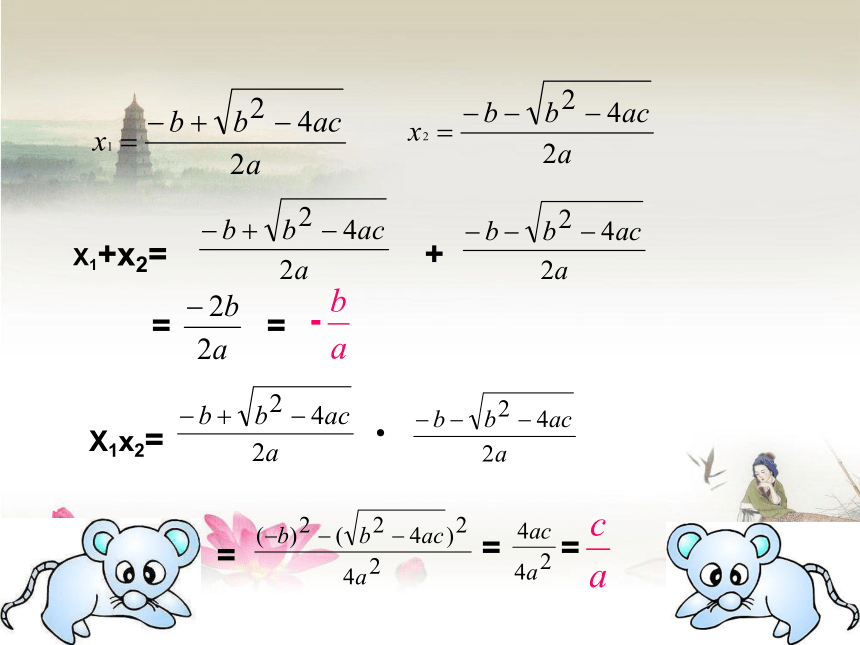





文档简介
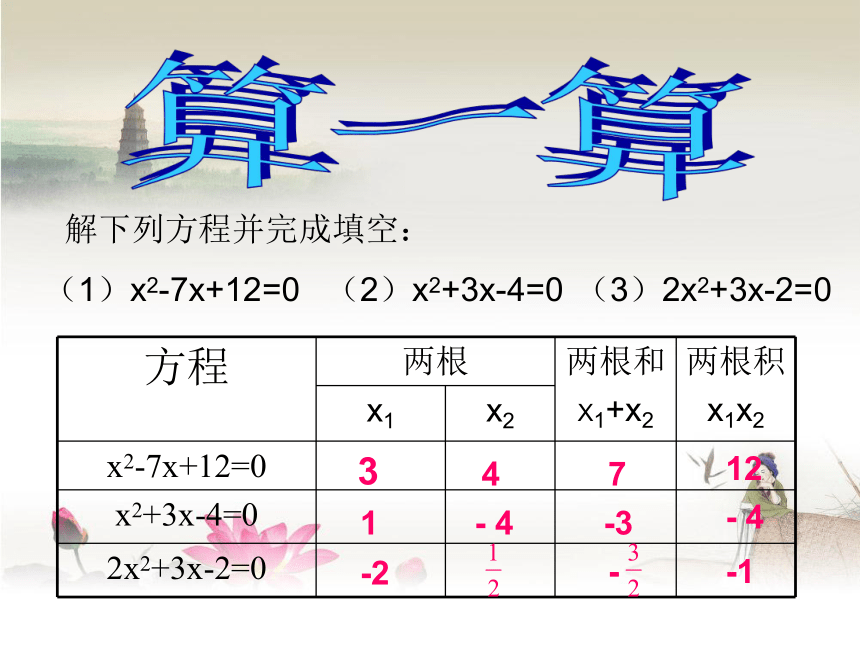
课件28张PPT。17.4 一元二次方程的根与系数的关系算一算(1)x2-7x+12=0(2)x2+3x-4=0(3)2x2+3x-2=0解下列方程并完成填空:341271-3- 4- 4-1--2X1+x2=+==-X1x2=●===一元二次方程的根与系数的关系:如果方程ax2+bx+c=0(a≠0)的两个根是X1,X2 ,那么X1+x2= , X1x2= -注:能用公式的前提条件为b2-4ac≥0 如果一元二次方程
的两个根分别是 、 ,那么:这就是一元二次方程根与系数的关系,也叫韦达定理.说一说:说出下列各方程的两根之和与两根之积:1、 x2 - 2x - 1=02、 2x2 - 3x + =03、 2x2 - 6x =04、 3x2 = 4x1+x2=2x1x2=-1x1+x2=x1+x2=3x1+x2=0x1x2=x1x2=0x1x2= -3、巩固练习:口答下列方程的两根只和与两根之积.1)x2-3x+1=02) x2-2x=23) 2x2-3x=04) 3x2=11.3.2.4.5.口答下列方程的两根之和与两根之积.判断对错,如果错了,说明理由.
1)2x2-11x+4=0两根之和11,两根之积4. 3) x2+2=0两根之和0,两根之积2. 4) x2+x+1=0两根之和-1,两根之积1. 2)4x2+3x=5两根之和 两根之积典型题讲解:例1、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值.解法一:设方程的另一个根为x1.由根与系数的关系,得x1 +2= k+1x1 ●2= 3k解这方程组,得x1 =-3 k =-2答:方程的另一个根是-3 , k的值是-2.典型题讲解:例、已知方程x2-(k+1)x+3k=0的一个根是2,
求它的另一个根及k的值.解法二:设方程的另一个根为x1.把x=2代入方程,得 4-2(k+1)+3k=0解这方程,得 k= - 2由根与系数的关系,得x1●2=3k即2 x1 =-6∴ x1 =-3答:方程的另一个根是-3 ,k的值是-2.例1:已知方程 2x2+kx-4=0的一个根是-4,求它的另一个根及k的值.答:方程的另一个根是 ,k的值是7.解:设方程的另一根为 ,则另外几种常见的求值设 x1、x2是方程x2-4x+1=0的两个根,则
x1+x2 = ___ x1x2 = ___,
x12+x22 = ;
( x1-x2)2 = ;
基础练习已知一元二次方程 的一个根为1 ,则方程的另一根为___,m=___:巩固提高补充规律:两根均为负的条件: x1+x2 且x1x2 . 两根均为正的条件: x1+x2 且x1x2 . 两根一正一负的条件: x1+x2 且x1x2 .
当然,以上还必须满足一元二次方程有根的条件:b2-4ac≥0 . 例1.
不解方程,求方程 的
两根的平方和、倒数和.运用根与系数的关系解题2、设x1.x2是方程2x2+4x-3=0的两个根,利用根与系数的关系,求下列各式的值.
(1)( x1+1)(x2+1)(2)— + —x1x2x1x23、
(1)若关于x的方程2x2+5x+n=0的一个根是-2,求它的另一个根及n的值.
(2)若关于x的方程x2+kx-6=0的一个根是-2,求它的另一个根及k的值.二、典型例题例题2:已知方程 x2=2x+1的两根为x1,x2,不解方程,求下列各式的值.
(1)(x1-x2)2 (2)x13x2+x1x23
(3)例题3:
设x1,x2是方程2x2-3x+m=0的两个根,且8x1-2x2=7,求m的值.例题4:
已知关于x的一元二次方程x2+(2k-1)x+k2=0有两个不相等的实数根,且方程的两根之和比两根之积7,求k的值.试一试1、已知方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值.2、设x1,x2是方程2x2+4x-3=0的两个根,求(x1+1)(x2+1)的值.解:设方程的另一个根为x1,则x1+1= ,∴ x1= ,又x1●1= ,∴ m= 3x1 = 16 解:由根与系数的关系,得x1+x2= - 2 , x1 · x2=∴ (x1+1)(x2+1) = x1 x2 + (x1+x2)+1 =-2+( )+1=2、已知关于X的方程mx2-(2m-1)x+m-2=0(m﹥0)
(1)此方程有实数根吗?
(2)如果这个方程的两个实数根分别为x1,x2,且 (x1-3)(x2-3)=5m,求m的值.拓广探索引申:若ax2?bx?c?0 (a?0 ??0)
(1)若两根互为相反数,则b?0;
(2)若两根互为倒数,则a?c;
(3)若一根为0,则c?0 ;
(4)若一根为1,则a?b?c?0 ;
(5)若一根为?1,则a?b?c?0;
(6)若a、c异号,方程一定有两个实数根.一正根,
一负根△>0
X1X2<0两个正根△≥0
X1X2>0
X1+X2>0两个负根△≥0
X1X2>0
X1+X2<0{{{小结
的两个根分别是 、 ,那么:这就是一元二次方程根与系数的关系,也叫韦达定理.说一说:说出下列各方程的两根之和与两根之积:1、 x2 - 2x - 1=02、 2x2 - 3x + =03、 2x2 - 6x =04、 3x2 = 4x1+x2=2x1x2=-1x1+x2=x1+x2=3x1+x2=0x1x2=x1x2=0x1x2= -3、巩固练习:口答下列方程的两根只和与两根之积.1)x2-3x+1=02) x2-2x=23) 2x2-3x=04) 3x2=11.3.2.4.5.口答下列方程的两根之和与两根之积.判断对错,如果错了,说明理由.
1)2x2-11x+4=0两根之和11,两根之积4. 3) x2+2=0两根之和0,两根之积2. 4) x2+x+1=0两根之和-1,两根之积1. 2)4x2+3x=5两根之和 两根之积典型题讲解:例1、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值.解法一:设方程的另一个根为x1.由根与系数的关系,得x1 +2= k+1x1 ●2= 3k解这方程组,得x1 =-3 k =-2答:方程的另一个根是-3 , k的值是-2.典型题讲解:例、已知方程x2-(k+1)x+3k=0的一个根是2,
求它的另一个根及k的值.解法二:设方程的另一个根为x1.把x=2代入方程,得 4-2(k+1)+3k=0解这方程,得 k= - 2由根与系数的关系,得x1●2=3k即2 x1 =-6∴ x1 =-3答:方程的另一个根是-3 ,k的值是-2.例1:已知方程 2x2+kx-4=0的一个根是-4,求它的另一个根及k的值.答:方程的另一个根是 ,k的值是7.解:设方程的另一根为 ,则另外几种常见的求值设 x1、x2是方程x2-4x+1=0的两个根,则
x1+x2 = ___ x1x2 = ___,
x12+x22 = ;
( x1-x2)2 = ;
基础练习已知一元二次方程 的一个根为1 ,则方程的另一根为___,m=___:巩固提高补充规律:两根均为负的条件: x1+x2 且x1x2 . 两根均为正的条件: x1+x2 且x1x2 . 两根一正一负的条件: x1+x2 且x1x2 .
当然,以上还必须满足一元二次方程有根的条件:b2-4ac≥0 . 例1.
不解方程,求方程 的
两根的平方和、倒数和.运用根与系数的关系解题2、设x1.x2是方程2x2+4x-3=0的两个根,利用根与系数的关系,求下列各式的值.
(1)( x1+1)(x2+1)(2)— + —x1x2x1x23、
(1)若关于x的方程2x2+5x+n=0的一个根是-2,求它的另一个根及n的值.
(2)若关于x的方程x2+kx-6=0的一个根是-2,求它的另一个根及k的值.二、典型例题例题2:已知方程 x2=2x+1的两根为x1,x2,不解方程,求下列各式的值.
(1)(x1-x2)2 (2)x13x2+x1x23
(3)例题3:
设x1,x2是方程2x2-3x+m=0的两个根,且8x1-2x2=7,求m的值.例题4:
已知关于x的一元二次方程x2+(2k-1)x+k2=0有两个不相等的实数根,且方程的两根之和比两根之积7,求k的值.试一试1、已知方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值.2、设x1,x2是方程2x2+4x-3=0的两个根,求(x1+1)(x2+1)的值.解:设方程的另一个根为x1,则x1+1= ,∴ x1= ,又x1●1= ,∴ m= 3x1 = 16 解:由根与系数的关系,得x1+x2= - 2 , x1 · x2=∴ (x1+1)(x2+1) = x1 x2 + (x1+x2)+1 =-2+( )+1=2、已知关于X的方程mx2-(2m-1)x+m-2=0(m﹥0)
(1)此方程有实数根吗?
(2)如果这个方程的两个实数根分别为x1,x2,且 (x1-3)(x2-3)=5m,求m的值.拓广探索引申:若ax2?bx?c?0 (a?0 ??0)
(1)若两根互为相反数,则b?0;
(2)若两根互为倒数,则a?c;
(3)若一根为0,则c?0 ;
(4)若一根为1,则a?b?c?0 ;
(5)若一根为?1,则a?b?c?0;
(6)若a、c异号,方程一定有两个实数根.一正根,
一负根△>0
X1X2<0两个正根△≥0
X1X2>0
X1+X2>0两个负根△≥0
X1X2>0
X1+X2<0{{{小结
