人教版八年级数学下册第16章二次根式的综合化简讲义(含解析)
文档属性
| 名称 | 人教版八年级数学下册第16章二次根式的综合化简讲义(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-22 00:00:00 | ||
图片预览



文档简介
考试后记
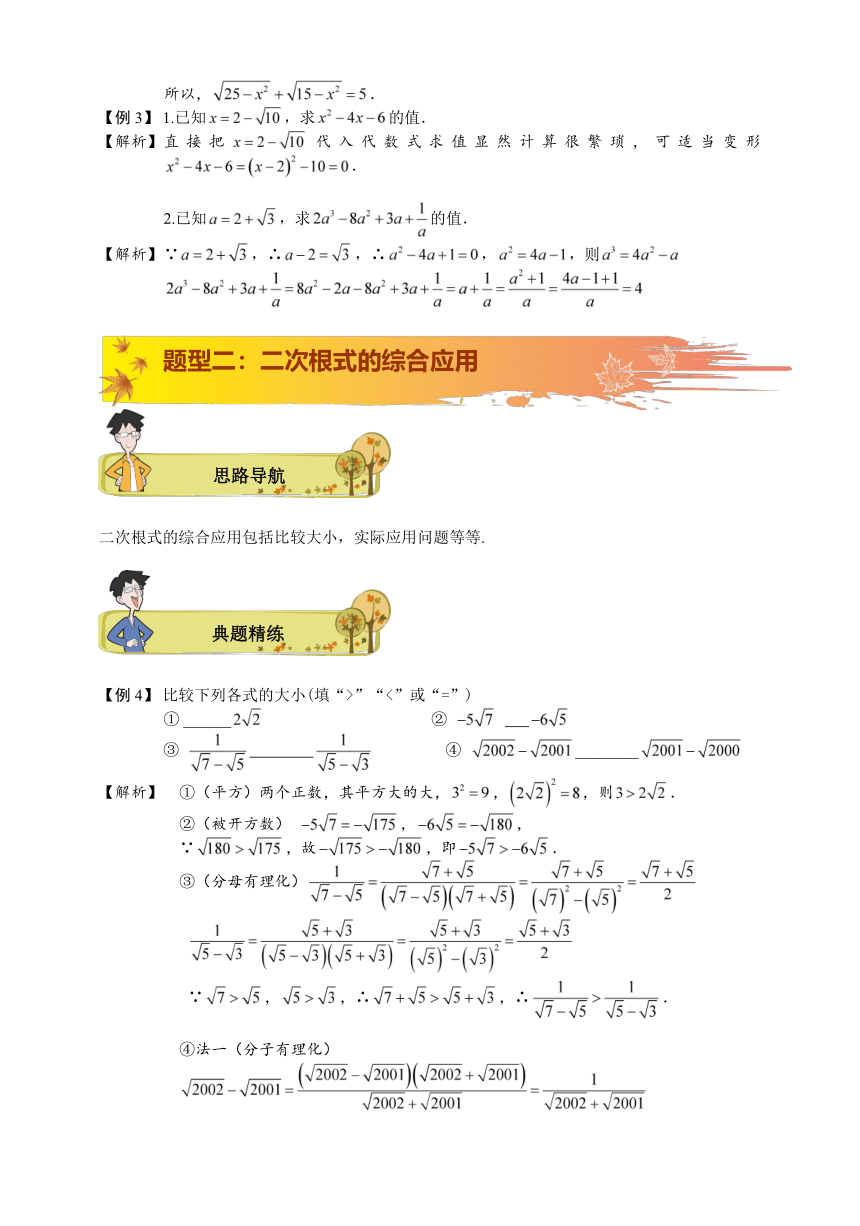
二次根式的化简求值,是中考以及各级各类竞赛中的常见题目,其常用的方法有约分法,裂项法,取倒法等等.
化简下列二次根式
1..
.
说明和互为倒数,故.
原式
2.
3.
此题是复合二次根式的化简,在初三的锐角三角函数中会涉及,老师还可练习,
此类题型的步骤为:⑴将二次根式化简为的形式
⑵将a拆成x+y,b拆成xy的形式
⑶
1. 已知,,求和.
;
2.已知,求的值.
,
,,
3.已知且,求的值.
∵
∴
原式=
4.其中,,求 的值.
原式.
例2精讲:、或、的应用
共轭根式:形如,的两个根式互称为共轭根式.
如果和互为共轭根式,那么和都是有理式.(其中为有理数)
通常情况下,将含有一个二次根式的代数式有理化的方法是乘以它的共轭根式.
解决根式问题,应当视情况将分母或分子进行有理化.
推广:、虽然不是共轭二次根式,但是同样是有理式,因此也可以用来帮助分母或分子有理化.
探究1、分母有理化
【变式1】计算:
【解析】原式;
探究2、分子有理化
【变式2】已知,,,,比较,,的大小.
【解析】分子有理化可直接得到答案,易得.
探究3、利用共轭根式和来化简求值
【变式3】已知,,求下列各式的值.⑴; ⑵.
【解析】∵,,∴,.
⑴.
⑵.
探究4、构造共轭根式进行配对
【变式4】已知,则的值是 .
【解析】设,;则,,
,
原式.
探究5、共轭根式求值
【变式5】已知.则的值为__________.
【解析】注意到,
所以,.
1.已知,求的值.
直接把代入代数式求值显然计算很繁琐,可适当变形.
2.已知,求的值.
∵,∴,∴,,则
二次根式的综合应用包括比较大小,实际应用问题等等.
比较下列各式的大小(填“>”“<”或“=”)
① ______ ②
③ ④ ________
①(平方)两个正数,其平方大的大,,,则.
②(被开方数) ,,
∵,故,即.
③(分母有理化)
∵,,∴,∴.
④法一(分子有理化)
∵,∴.
法二(倒数法),,
已知、均为有理数,并满足等式,求、的值.
【解析】由已知条件可得,所以,即,.
若,,,求证:.
待证不等式左边的根式,让人联想起直角三角形中斜边的表达式;而其右边为的倍,又与正方形的对角线有关.我们借助几何图形给予证明.
作出以为边长的正方形,分别在两边上截取线段、、,如图,则,,,
而,显然,由,可得原不等式成立.
已知,,求的值.
∵,
,
∴
∴.
已知,求的值.
直接代入肯定麻烦,先对已知条件进行变形.
,,,即.
下面采用降幂(次):
.
已知,求及的值.
,∵ ∴
∵ ∴
又∵
∴
设三所学校、、分别位于一个等边三角形的三个顶点处,现是网络时代,要在三个学校之间铺设通讯电缆,小张同学设计了三种连接方案,如图所示,方案甲:;方案乙:(为中点);方案丙:(为三角形三条高的交点),请你帮助计算一下哪种方案线路最短?
设,则,,在中,,.
方案甲:;方案乙:;
方案丙:
所以,.
题型一 二次根式的化简与求值 巩固练习
已知,求的值. (四中期中)
当时,
原式
.
若求的值
由得即两边平方,得
∴原式=
题型二 二次根式的综合应用 巩固练习
已知n是一个正整数,是整数,则n的最小值是( )
A.3 B.5 C.15 D.25
C
某电力公司为了改善农村用电电费过高的问题,准备在各地农村进行电网改造,富康乡有四个村庄,,,正好位于一个正方形的四个顶点,现计划在四个村庄联合架设一条线路,有四种架设方案,如图中的实线部分,请你帮助计算一下,哪种架设方案最省电线.
(以下数据可供参考:,,)
方案4最省钱.
若表示不超过的最大整数(如等),则
_________________.
2000
已知,求 ⑴; ⑵. (宣武期末)
由题意得
⑴ 原式 ⑵ 原式
先化简,再求值:,其中,.
.
当,时,
原式
试比较与的大小.
,.
显然,.
