人教版数学八年级下册 18.2.1 矩形的性质 课件 共24张PPT
文档属性
| 名称 | 人教版数学八年级下册 18.2.1 矩形的性质 课件 共24张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 621.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-14 07:27:39 | ||
图片预览





文档简介
课件24张PPT。18.2.1矩形(1)一个角是
直角两组对边
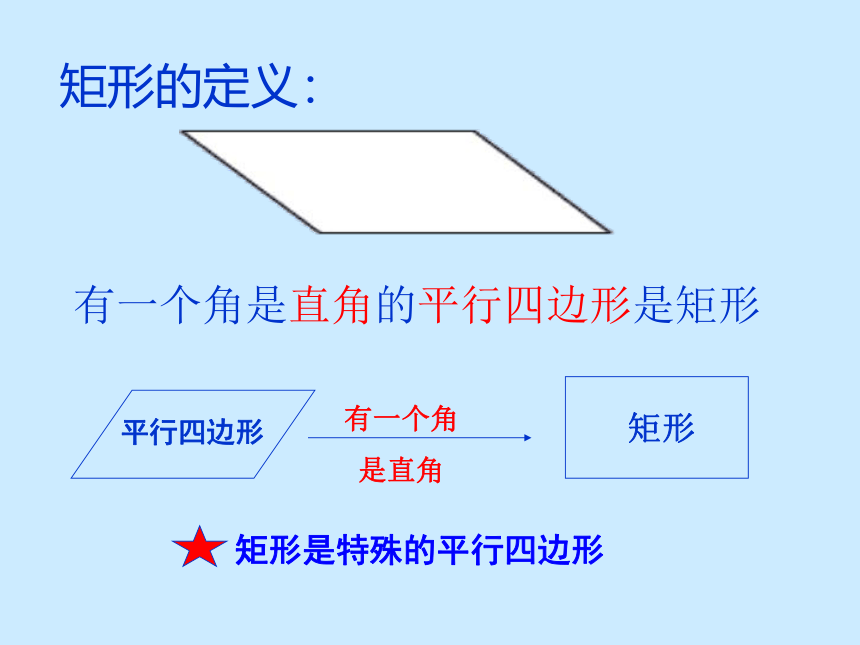
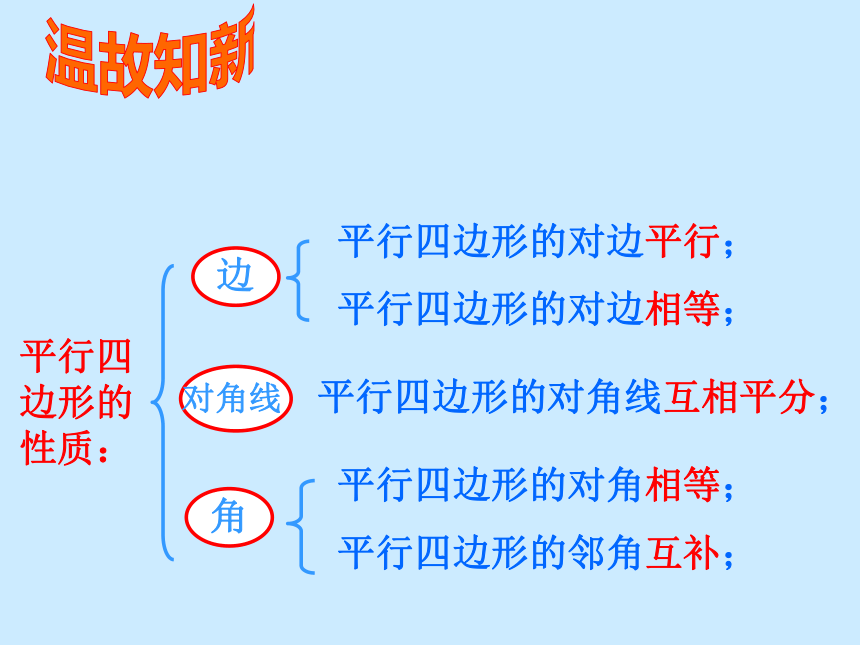
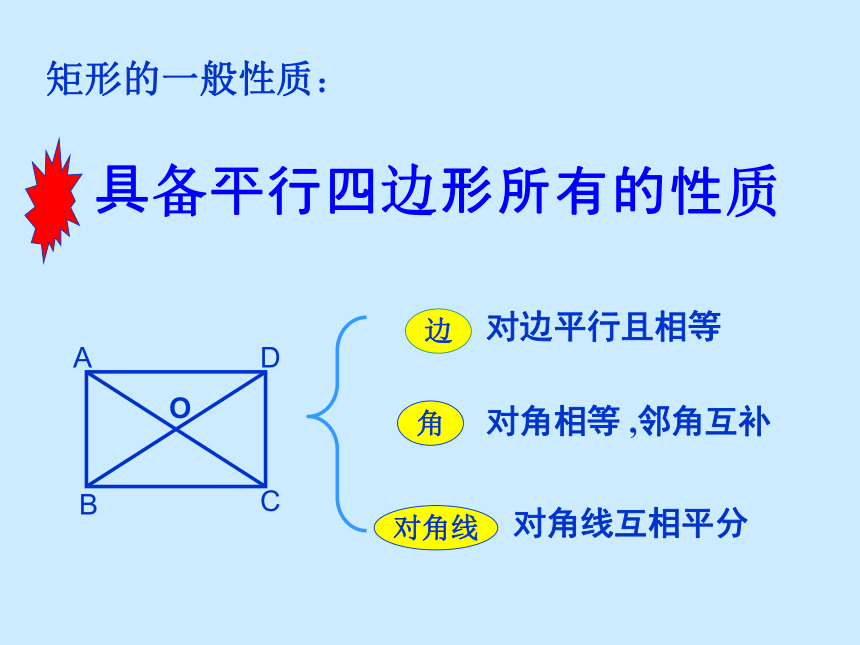
分别平行矩形情景创设我们知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况,这堂课我们就来研究一种恃殊的平行四边形—— 矩形有一个角是直角的平行四边形是矩形矩形的定义:生活中的实例讨论一下矩形是平行四边形吗?平行四边形有什么性质?矩形有什么性质?平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分; 温故知新对边平行且相等对角相等 ,邻角互补对角线互相平分矩形的一般性质:探索新知:
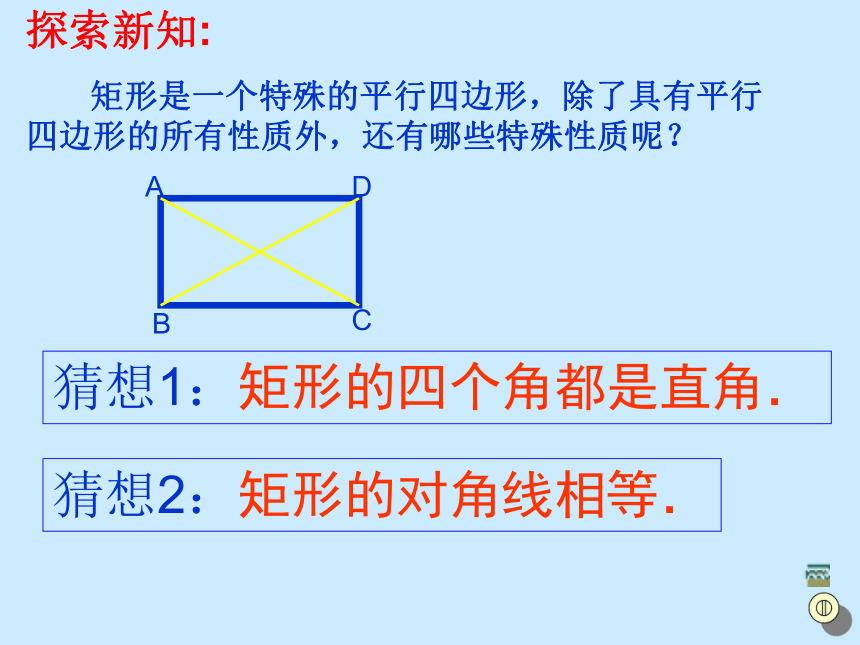
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD 1:矩形的四个角都是直角已知:四边形ABCD是矩形,
∠B=90°
求证:∠A=∠B=∠C=∠D=90°DCBA性质命题证明:∵四边形ABCD是平行四边形, ∠B=90°
∴∠B=∠D=90° ∠B+∠C=180 °
∴∠B+ ∠ A=180°
∴∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形,求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 2:矩形的对角线相等.性质命题矩形的 两条对角线互相平分矩形的两组对边分别相等矩形的两组对边分别平行矩形的四个角都是直角矩形 的两条对角线相等边对角线角数学语言∵四边形ABCD是矩形∴AD = BC ,CD = AB∴AD ∥BC ,CD ∥AB∴AC= BD ∴AO= CO ,OD = OB矩形的性质OABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏如图,在任意的矩形ABCD中,AC,BD相交于O,那么BO与AC有怎样的数量关关系?Rt⊿ABC中,BO是Rt⊿ABC的什么线?
由此你能得到什么结论?
ABCDO还能得到什么结论?直角三角形的性质: 直角三角形斜边上的中线等于斜边的一半。 数学语言:
在Rt三角形ABC中
∵∠ABC=90°
BO是AC边的中线
ABCO
回忆一下,之前学过的,在直角三角形中什么情况下还有什么边是等于斜边的一半?例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)O 矩形具有而一般平行四边形不
具有的性质是 ( ) A.对角相等B.对边相等C.对角线相等 D.对角线互相平分C小试身手四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知AC=10㎝,BC=6㎝,则矩形的周长=____ cm
矩形的面积=_______ ㎝2
3. 若已知 ∠DOC=120°,AD=6㎝,则AC= _____cm510124828小试身手(1)如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD面积的( ).
A. B. C . D.
. .4.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线若BD=3㎝则AC= ㎝
2 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝,6510小试身手能力提高:如图,矩形的一条对角线长为8cm,两条对角线的一个交角为120°,求矩形的边长.解:∵∠AOB=120°,
∴∠AOD=180°-∠AOB=60° ∵AC=BD=8 又∵AC,BD互相平分,∴AO=BO. ∴△AOD是等边三角形。 ∴AD=AO=1/2AC=4 ∵四边形ABCD是矩形,∴∠BAD=90° 在△ABD中,由勾股定理,得 AB=√(BD2-AD2)=√48=4 √3邻边:互相垂直四个角都是直角 互相平分
相 等
(1)边:(2)角:(3)对角线:(共性)(共性)(个性)(个性)(个性)(共性)O矩形特征有一个内角
是直角1.矩形的定义:2.矩形的性质:我的成果展①边:
②角
③对角线
④对称性对边平行且相等
四个角都是直角
对角线平分且相等
既是轴对称图形和又是中心对称图形
3.直角三角形的一个性质 直角三角形斜边上的中线等于斜边的一半。
直角两组对边
分别平行矩形情景创设我们知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况,这堂课我们就来研究一种恃殊的平行四边形—— 矩形有一个角是直角的平行四边形是矩形矩形的定义:生活中的实例讨论一下矩形是平行四边形吗?平行四边形有什么性质?矩形有什么性质?平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分; 温故知新对边平行且相等对角相等 ,邻角互补对角线互相平分矩形的一般性质:探索新知:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD 1:矩形的四个角都是直角已知:四边形ABCD是矩形,
∠B=90°
求证:∠A=∠B=∠C=∠D=90°DCBA性质命题证明:∵四边形ABCD是平行四边形, ∠B=90°
∴∠B=∠D=90° ∠B+∠C=180 °
∴∠B+ ∠ A=180°
∴∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形,求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 2:矩形的对角线相等.性质命题矩形的 两条对角线互相平分矩形的两组对边分别相等矩形的两组对边分别平行矩形的四个角都是直角矩形 的两条对角线相等边对角线角数学语言∵四边形ABCD是矩形∴AD = BC ,CD = AB∴AD ∥BC ,CD ∥AB∴AC= BD ∴AO= CO ,OD = OB矩形的性质OABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏如图,在任意的矩形ABCD中,AC,BD相交于O,那么BO与AC有怎样的数量关关系?Rt⊿ABC中,BO是Rt⊿ABC的什么线?
由此你能得到什么结论?
ABCDO还能得到什么结论?直角三角形的性质: 直角三角形斜边上的中线等于斜边的一半。 数学语言:
在Rt三角形ABC中
∵∠ABC=90°
BO是AC边的中线
ABCO
回忆一下,之前学过的,在直角三角形中什么情况下还有什么边是等于斜边的一半?例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)O 矩形具有而一般平行四边形不
具有的性质是 ( ) A.对角相等B.对边相等C.对角线相等 D.对角线互相平分C小试身手四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知AC=10㎝,BC=6㎝,则矩形的周长=____ cm
矩形的面积=_______ ㎝2
3. 若已知 ∠DOC=120°,AD=6㎝,则AC= _____cm510124828小试身手(1)如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD面积的( ).
A. B. C . D.
. .4.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线若BD=3㎝则AC= ㎝
2 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝,6510小试身手能力提高:如图,矩形的一条对角线长为8cm,两条对角线的一个交角为120°,求矩形的边长.解:∵∠AOB=120°,
∴∠AOD=180°-∠AOB=60° ∵AC=BD=8 又∵AC,BD互相平分,∴AO=BO. ∴△AOD是等边三角形。 ∴AD=AO=1/2AC=4 ∵四边形ABCD是矩形,∴∠BAD=90° 在△ABD中,由勾股定理,得 AB=√(BD2-AD2)=√48=4 √3邻边:互相垂直四个角都是直角 互相平分
相 等
(1)边:(2)角:(3)对角线:(共性)(共性)(个性)(个性)(个性)(共性)O矩形特征有一个内角
是直角1.矩形的定义:2.矩形的性质:我的成果展①边:
②角
③对角线
④对称性对边平行且相等
四个角都是直角
对角线平分且相等
既是轴对称图形和又是中心对称图形
3.直角三角形的一个性质 直角三角形斜边上的中线等于斜边的一半。
