第5章 数据的频率分布单元检测试卷(含解析)
文档属性
| 名称 | 第5章 数据的频率分布单元检测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-14 17:10:30 | ||
图片预览



文档简介
湘教版八年级下第5章数据的频率分布单元检测试卷
班级_____________考号______________姓名_______________总分_________________
一、选择题(12小题,每题3分,共36分)
1.如图是某班一次数学测试成绩的频数直方图,则成绩在分范围内的学生共有
A.24人 B.10人 C.14人 D.29人
2.将“我爱北京天安门”用拼音可写成“WOAIBEIJINGTIANANMEN”,其中字母“I”出现的频率是( )
A.0.5 B.0.4 C.0.3 D.0.2
3.小敏统计了全班50名同学最喜欢的学科(每个同学只选一门学科).统计结果显示:最喜欢数学和科学的频数分别是13和10.最喜欢语文和英语的人数的频率分别是0.3和0.2,其余的同学最喜欢社会,则下列叙述错误的是( )
A.最喜欢语文的人数最多
B.最喜欢社会的人数最少
C.最喜欢数学的人数和最喜欢语文的人数之和超过总人数的一半
D.最喜欢科学的人数比最喜欢英语的人数要少
4.某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如图所示的统计图. 甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数的比为4∶17∶15,则本次测试共抽调的人数为( )
A.120 B.150 C.180 D.无法确定
5.已知20个数据如下:
25 21 29 30 24 25 29 28 27 23
27 26 22 24 28 26 25 23 25 27
对这些数据进行分析,其中24.5~26.5这一组的频率是( )
A.0.40 B.0.30 C.0.55 D.0.25
6.下表为某公司200名职员年龄的人数分配表,其中36~42岁及50~56岁的人数因污损而无法看出.若36~42岁及50~56岁职员人数的相对次数分别为a%、b%,则a+b之值为何?( )
年龄
22~28
29~35
36~42
43~49
50~56
57~63
次数
6
40
42
2
A.10 B.45 C.55 D.99
7.某次数学测验,抽取部分同学的成绩(得分为整数)整理制成频数分布直方图,如图所示.根据图示信息,下列描述不正确的是( )
A.共抽取了50人
B.90分以上的有12人
C.80分以上的所占的百分比是60%
D.60.5~70.5分这一分数段的频数是12
8.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:则通话时间不超过15min的频率为( )
通话时间x/min
0<x≤5
5<x≤10
10<x≤15
15<x≤20
频数(通话次数)
20
16
9
5
A.0.1 B.0.4 C.0.5 D.0.9
9.在某次人才交流会上,应聘人数和招聘人数分别居前5位的行业列表如下:
如果用同一行业应聘人数与招聘人数比值的大小来衡量该行业的就业情况,那么根据表中数据,对上述行业的就业情况判断正确的是( )
A.计算机行业好于其它行业 B.贸易行业好于化工行业
C.机械行业好于营销行业 D.建筑行业好于物流行业
10.列频数分布表考查50名学生年龄时,这些学生的年龄落在5个小组中,第一、二、三、五组的数据个数分别是1,9,15,5,则第四组的频数是( ).
A.10 B.9 C.15 D.20
11.某班学生在颁奖大会上得知该班获得奖励的情况如下表:
三好学生
优秀学生干部
优秀团员
市级
3
2
3
校级
18
6
12
已知该班共有28人获得奖励,其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
A.3项 B.4项 C.5项 D.6项
12.为了了解某地区八年级男生的身高情况,从其中一个学校选取容量为50的样本,50名男生的身高(单位:cm)分组情况如下表所示,则表中a,b的值分别是( )
分组
147.5~155.5
155.5~163.5
163.5~171.5
171.5~179.5
频数
10
18
a
频率
0.3
b
A.15,7 B.15,0.14 C.0.14,15 D.7,15
二、填空题(6小题,每题3分,共18分)
13.在一块试验田里抽取1000个小麦穗,考察它们的长度(单位:cm),从频率分布表中看到,样本数据落5.75cm~6.05cm之间的频率是0.36,于是可以估计,在这块土地里,长度在5.75cm~6.05cm之间的麦穗约占________
14.一次数学测试后,某班50名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、8,则第5组的频率是_____________.
15.有一个样本共有50个数据,分成若干组后,其中有一小组的频率是0.4,则该组的频数是_____.
16.一组数据,最大值与最小值的差为16,取组距为4,则组数为_____.
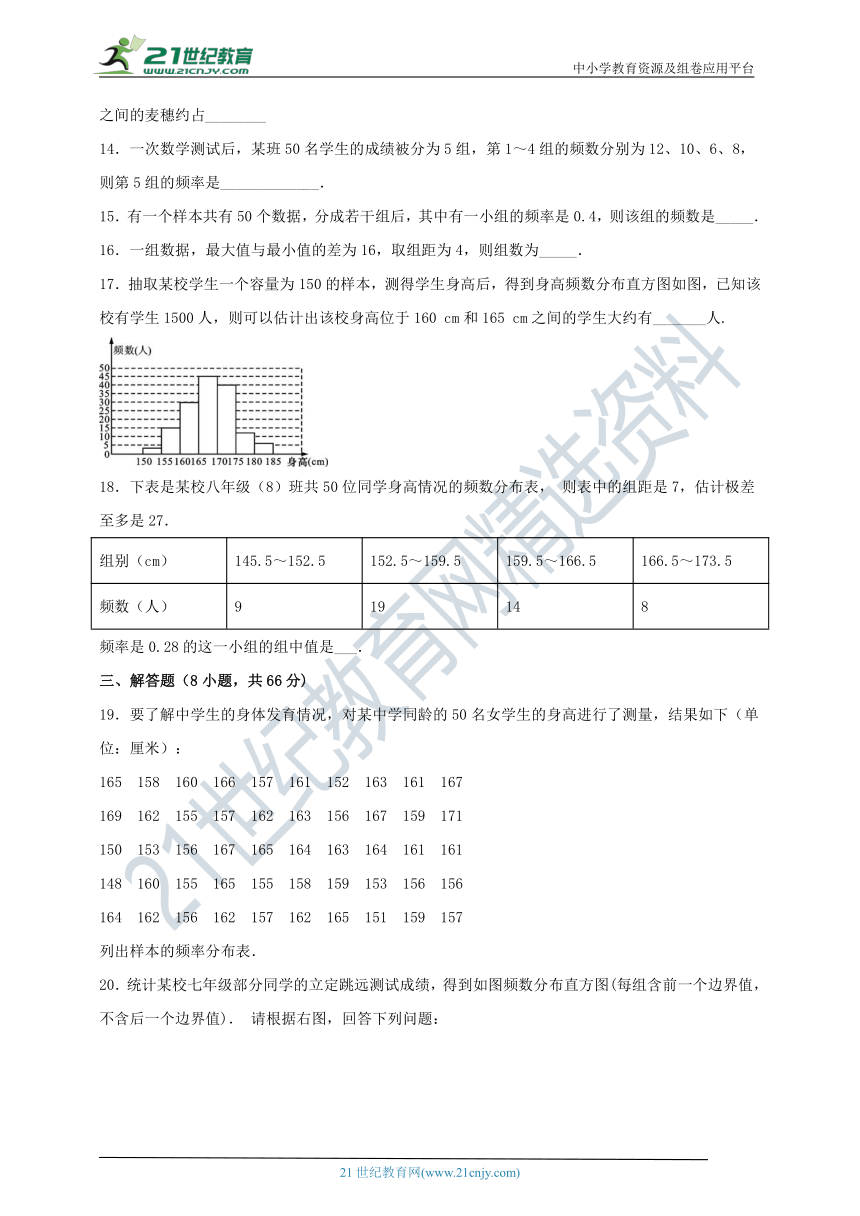
17.抽取某校学生一个容量为150的样本,测得学生身高后,得到身高频数分布直方图如图,已知该校有学生1500人,则可以估计出该校身高位于160 cm和165 cm之间的学生大约有_______人.
18.下表是某校八年级(8)班共50位同学身高情况的频数分布表,则表中的组距是7,估计极差至多是27.
组别(cm)
145.5~152.5
152.5~159.5
159.5~166.5
166.5~173.5
频数(人)
9
19
14
8
频率是0.28的这一小组的组中值是___.
三、解答题(8小题,共66分)
19.要了解中学生的身体发育情况,对某中学同龄的50名女学生的身高进行了测量,结果如下(单位:厘米):
165 158 160 166 157 161 152 163 161 167
169 162 155 157 162 163 156 167 159 171
150 153 156 167 165 164 163 164 161 161
148 160 155 165 155 158 159 153 156 156
164 162 156 162 157 162 165 151 159 157
列出样本的频率分布表.
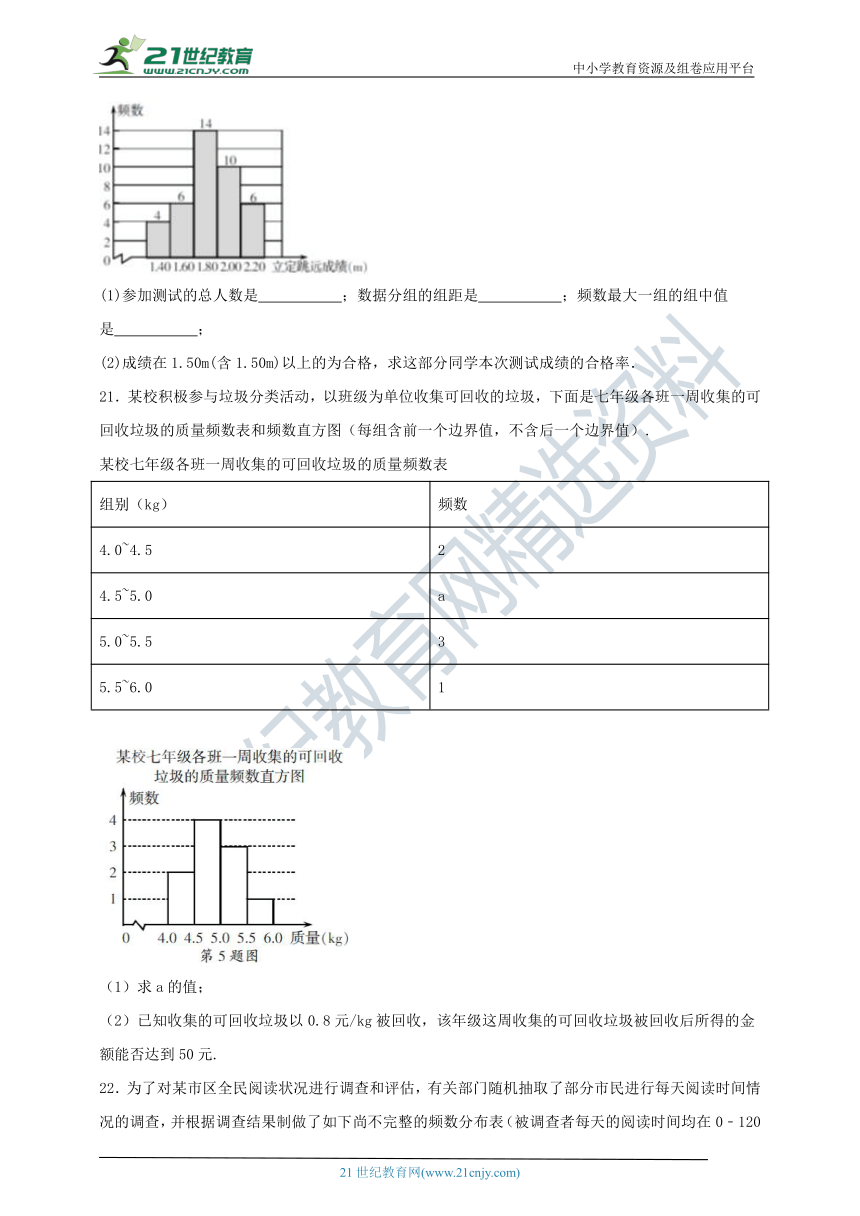
20.统计某校七年级部分同学的立定跳远测试成绩,得到如图频数分布直方图(每组含前一个边界值,不含后一个边界值). 请根据右图,回答下列问题:
(1)参加测试的总人数是 ;数据分组的组距是 ;频数最大一组的组中值是 ;
(2)成绩在1.50m(含1.50m)以上的为合格,求这部分同学本次测试成绩的合格率.
21.某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg)
频数
4.0~4.5
2
4.5~5.0
a
5.0~5.5
3
5.5~6.0
1
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.
22.为了对某市区全民阅读状况进行调查和评估,有关部门随机抽取了部分市民进行每天阅读时间情况的调查,并根据调查结果制做了如下尚不完整的频数分布表(被调查者每天的阅读时间均在0﹣120分钟之内)
阅读时间x(分钟)
0≤x<30
30≤x<60
60≤x<90
90≤x≤120
频数
450
400
m
50
频率
0.45
0.4
0.1
n
(1)被调查的市民人数为多少,表格中,m,n为多少;
(2)补全频数分布直方图;
(3)某市区目前的常住人口约有118万人,请估计该市区每天阅读时间在60~120分钟的市民大约有多少万人?
23.某地区为了增强市民的法制观念,抽调了一部分市民进行了一次知识竞赛,竞赛成绩(得分数取整数)进行整理后分成五组,并绘制成频数分布直方图,请结合图提供的信息,解答下列问题:
(1)抽取了多少人参加竞赛?
(2)61~71这一分数段的频数和频率分别是多少?
(3)根据统计图,请你提出一个问题,并回答你所提出的问题.
24.南京某中学为了迎接世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:
请结合图表完成下列各题:
(1)求表中a的值:
(2)请把频数分布直方图补充完整:
(3)若测试成绩不低于90分的同学可以获得世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”?
25.某市第三中学组织学生参加生命安全知识网络测试.小明对七年级二班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图:
根据图表中的信息解答下列问题:
(1)七年级二班学生的人数为________,频数分布表中的值为________;
(2)已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上(含80分)为优秀,佔计该市本次测试成绩达到优秀的人数;
(3)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因。
26.某校九年级学生共900人,为了解这个年级学生的体能,从中随机抽取部分学生进行1min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理.下面是这四名同学提供的部分信息:甲:将全体测试数据分成6组绘成直方图(如图);乙:跳绳次数不少于105次的同学占96%;丙:第①、②两组频率之和为0.12,且第②组与第⑥组频数都是12;丁:第②、③、④组的频数之比为4∶17∶15.
根据这四名同学提供的材料,请解答如下问题:
(1)这次跳绳测试共抽取多少名学生?各组有多少人?
(2)如果跳绳次数不少于135次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为多少?
(3)以每组的组中值(每组的中点对应的数据)作为这组跳绳次数的代表,估计这批学生1min跳绳次数的平均值.
参考答案
1.【考点】频数分布直方图
【分析】根据直方图给出的数据,把成绩在分范围内的学生人数相加即可得出答案.
解:成绩在分范围内的学生共有:人, 故选:A.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
2.【考点】频率的计算
【分析】数出共20个字母,I出现了4次,用4÷20即可求出频率.
解:依题意4÷20=0.2,故选D.
【点睛】此题主要考察频率的计算.
3.【考点】频数和频
【分析】依据,可求出最喜欢语文和英语的人数,进而求出最喜欢社会的人数,然后逐个判断即可.
解:∵最喜欢语文和英语的人数的频率分别是0.3和0.2,总体为50,
∴喜欢语文的人数为0.3×50=15人,喜欢英语的人数为0.2×50=10人,则最喜欢社会的人数为50?13?10?15?10=2人,则最喜欢数学的人数和最喜欢语文的人数之和为13+15=28人,超过总人数的一半,故A、B、C正确.
故选D.
【点睛】这是一道考查频数和频率的题目,解题关键在于掌握频数和频率与总体的关系:,.
4.【考点】频数直方图
【分析】各小组频数之和等于数据总和,各小组的频率之和等于1;易知第二组的频率0.08;再由频数为12,得出总人数.
解:∵跳绳次数不少于100次的同学占96%,
∴第一组的频率为1-0.96=0.04,
∴第二组的频率为0.12-0.04=0.08,
故总人数为120.08=150(人),
故选B.
【点睛】此题主要考察频数直方图.
5.【考点】频率、频数
【分析】首先正确数出在24.5-26.5这组的数据的频数;再根据进行计算.
解:其中在24.5-26.5组的共有6个,
则24.5-26.5这组的频率是6÷20=0.30.
故选B.
【点睛】本题考查频率、频数的关系,难度不大,注意正确查出相关数据的人数及名单频数,根据的关系解答.
6.【考点】表格数据的读取
【分析】先求出36~42岁及50~56岁的职员人数和,再求出他们的占比.
解:由表知36~42岁及50~56岁的职员人数共有,
200﹣6﹣40﹣42﹣2=110人,
所以,a%+b%=×100%=55%,
所以a+b=55.
故选:C.
【点睛】此题主要考查表格数据的读取,解题的关键是先求出人数之和.
7.【考点】读频数分布直方图
【分析】根据表中提供的数据分别进行计算,即可找出描述不正确的选项.
解:A、抽样的学生共有:4+10+18+12+6=50人,故本选项正确,不符合题意;
B. 90分以上的有12人,故本选项正确,不符合题意;
C. 80分以上的所占的百分比是=60%;故本选项正确,不符合题意;
D. 60.5~70.5分这一分数段的频数是10,故本选项错误,符合题意;
故选D.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
8.【考点】频数分布表
【分析】用不超过15分钟的通话次数除以所有的通话次数即可求得通话时间不超过15分钟的频率.
解:∵不超过15分钟的通话次数为20+16+9=45次,通话总次数为20+16+9+5=50次, ∴通话时间不超过15min的频率为 =0.9, 故选:D.
【点睛】本题考查频数分布表的知识,解题关键是了解频率=频数÷样本容量,难度不大.
9.【考点】统计表
【分析】通过统计表可以得到应聘人数与招聘人数,进而通过计算应聘人数与招聘人数的比值大小来衡量该行业的就业情况,比值越小越容易就业,比值越大越不容易就业,通过计算即可求解.
解:计算机行业比值为1.84;机械行业比值为2.29;营销行业比值为1.50;建筑行业比值<≈0.86;化工行业比值<≈0.91;而物流行业比值>≈1.23,贸易行业的比值<≈0.90,
∴计算机行业比值不是最小的,因此不是最优的,故A错误;贸易行业与化工行业不确定大小,故B错误;机械行业比值大于营销行业比值,故营销行业优于机械行业,故C错误;建筑行业比值小于物流行业比值,故D正确. 故选:D.
【点睛】本题考查了统计部分的有关知识,解题关键是通过计算应聘人数与招聘人数的比值大小来衡量该行业的就业情况.
10.【考点】频数
【分析】由五个小组的频数总和等于50即可算出第四组的频数.
解:∵第一、二、三、五组的数据个数分别是1,9,15,5,
∴第四小组的频数是50﹣(1+9+15+5)=20.
故选:D.
【点睛】本题是对频数的考查,各小组频数之和等于数据总和.
11.【考点】频数分布表
【分析】求得除获两项奖励的人数,以及这些人获得的奖的项数即可作出判断.
解:各项频数的和是:2+3+3+15+9+12=44; 获得两项奖励的有13人,则奖数是2×13=26; 44-26=18, 28-13=15, 则获奖最多的一名学生的获奖项数是:1+(18-15)=4. 故答案是:4.
【点睛】本题考查了频数分布表,分清各项数据的关系是本题的解题关键.
12.【考点】频率分布表
【分析】根据样本容量为50,由频率与频数的关系可求出a=15,根据前两组的频数求出学生身高为171.5~179.5的频数,再利用频率与频数的关系即可求出b=0.14.
解:∵样本容量为50,
∴a=50×0.3=15;
∴学生身高为171.5~179.5的频数为:50-10-18-15=7,
∴b=7÷50=0.14.
故选B.
【点睛】本题考点是频率分布表,考查对频率分布表结构的认识,以及其中数据的意义.是统计中的基本题型.
13.【考点】频率可以估计事件
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近.
解:∵抽取1000个麦穗考查它的长度落在5.75~6.05之间的频率为0.36,
∴这块田里长度为5.75~6.05cm之间的麦约占36%.
故本题答案为:36%.
【点睛】本题考查了样本估计总体,利用了用大量试验得到的频率可以估计事件的概率.
14.【考点】频率,频数之间的关系
【分析】根据第1~4组的频数,求出第5组的频数,即可确定出其频率.
解:根据题意得:50?(12+10+6+8)=50?36=14,
则第5组的频率为14÷50=0.28,
故答案为:0.28.
【点睛】考查频率,频数之间的关系,掌握它们之间的关系式是解题的关键.
15.【考点】频数与频率
【分析】由公式:频率=,得:频数=总数据×频率,即可求出答案.
解:由题意得:
该组的频数为:50×0.4=20.
故答案为:20.
【点睛】本题考查了频数与频率,难度一般,能够灵活运用频率=这一公式是解决本题的关键.
16.【考点】组数
【分析】在样本数据中最大值与最小值的差为16,已知组距为4,那么由于16÷4=4,且要求包含两个端点在内;故可以分成5组.
解:∵16÷4=4,
∴组数为5,
故答案为:5.
【点睛】本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
17.【考点】频数分布直方图
【分析】根据频率直方图的意义,由用样本估计总体的方法可得样本中160~165的人数,进而可得其频率;计算可得1500名学生中身高位于160cm至165cm之间的人数
解:由题意可知:150名样本中160~165的人数为30人,则其频率为,
则1500名学生中身高位于160cm至165cm之间大约有1500×=300人.
故答案为:300.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;同时本题很好的考查了用样本来估计总体的数学思想.
18.【考点】频率与频数
【分析】先求出频率是0.28的一组的频数,再求出其组中值即可.
解:频率是0.28的一组的频数=50×0.28=14人,
∴这一组是159.5﹣166.5组,
∴组中值为=163.
故本题答案为:163.
【点睛】此题主要考查频率与频数的关系,解题的关键是根据频率求出频数.
19.【考点】列频率分布表
【分析】据题意,计算极差,确定组距与组数,列频率分布表,
解:①计算极差为:171-148=23, ②确定组距与组数:以4为组距,23≈6,可以分为6组; ③列频率分布表,如下;
小组
频数
频率
(147.5,151.5)
3
0.06
(151.5,155.5)
6
0.12
(155.5,159.5)
14
0.28
(159.5,163.5)
14
0.28
(163.5,167.5)
11
0.22
(167.5,171.5)
2
0.04
总计
50
1.00
【点睛】本题考查了列频率分布表,是基础题目.熟练掌握画频率分布直方图的基本步骤是解题的关键。
20.【考点】条形统计图运用
【分析】根据条形统计图即可得到每一组的人数,根据每组的组中值即可确定组距,据此即可作出判断.
解:(1)4+6+14+10+6=40人 1.60-1.40=0.2m 1.80m ;
(2)(6+14+10+6)÷40=90%.
【点睛】本题考查的是条形统计图运用,解题关键是读懂统计图,从统计图中得到必要的信息.
21.【考点】条形统计图运用
【分析】根据条形统计图的应用来解答即可.
解:(1)观察频数分布直方图可得出a=4;
(2)每组含前一个边界值,不含后一个边界值,
∵2×4.5+4×5+3×5.5+1×6=51.5kg,
∴总质量小于51.5kg,∵51.5×0.8=41.2元<50元,
∴该年级这周的可回收垃圾被回收后所得金额不能达到50元.
【点睛】此题主要考察条形统计图的应用.
22.【考点】频数分布直方图
【分析】(1)根据0≤x<30的频数和频率先求出总人数,用总人数乘以60≤x<90的频率求出m,用90≤x≤120的频数除以总人数求出n;
(2)根据(1)求出的总人数,补全统计图即可;
(3)用常住人口数乘以阅读时间在60~120 分钟的人数的频率即可得出答案.
解:(1)根据题意得:被调查的市民人数为=1000(人),
m=1000×0.1=100,
n==0.05;
(2)根据(1)补图如下:
(3)根据题意得:118×(0.1+0.05)=17.7(万人)
估计该市区每天阅读时间在 60~120分钟的市民大约有17.7万人.
故答案为:(1)1000,100,0.05;(2)根据(1)补图见解析;(3)估计该市区每天阅读时间在 60~120分钟的市民大约有17.7万人.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
23.【考点】频数直方图的应用
【分析】(1)在直方图中找到各组的人数再相加即得总人数;(2)根据直方图找到61~71这一分数段的频数为12,再求出频率即可.(3)根据直方图得出成绩在80.5分以上有15人,若成绩在80.5分以上的同学获奖,则可求出获奖率.
解:(1)3+6+9+12+18=48(人),即抽取了48人参加竞赛.
(2)61~71这一分数段的频数为12,频率为=.
(3)答案不唯一.如果成绩在80.5分以上的同学获奖,那么此知识竞赛活动参赛市民的获奖率是多少?解答:≈0.31=31%.
【点睛】此题主要考察频数直方图的应用.
24.【考点】频数分布直方图
【分析】(1)用随机抽查的总数减去第1组、第2组、第4组、第5组的频数即可求出a的值;
(2)根据(1)求出的a的值和第4组的人数即可补全统计图;
(3)用全年级的总人数乘以成绩不低于90分的同学所占的百分比即可得出答案.
解:(1)a=100﹣(8+16+32+20)=24;
(2)根据题意补图如下:
(3)根据题意得:
600× 20% =120(人),
答:该校九年级有 120 人可以获得“乒宝”.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
25.【考点】频数分布表和扇形统计图
【分析】(1)根据数据总数=代入计算,求出七年级2班学生的人数; (2)先计算优秀的百分比,再与80000相乘即可; (3)取的样本不足以代表全市总中学的总体情况.
解:(1)17÷34%=50(人),a=24%×50=12, 答:九年级2班学生的人数为50人;
(2)E:14÷50=28%, (28%+24%)×80000=52×800=41600(人), 答:估计该市本次测试成绩达到优秀的人数为41600人; (3)全市参加本次测试的中学生中,成绩达到优秀有56?320人;而样本中估计该市本次测试成绩达到优秀的人数为41600人,原因是:小明对第三中学九年2班全体学生的测试成绩取的样本不足以代表全市总中学的总体情况,所以会出现较大偏差.
【点睛】本题考查了数据的收集与整理,根据频数分布表和扇形统计图可以将大量数据分类,结果清晰,一目了然地表达出来,熟练掌握公式是做好本题的关键:数据总数=,各组频数和=总数据.
26.【考点】频率、频数的概念,频数直方图
【分析】(1)由直方图中,各组频率之和为1,可求出②③组的频率,再根据②③组的频数结合频数与频率的关系可求得总数;
(2)从图中可以看出,第⑤⑥组的频数在135以上,故这两组优秀,所以用它们的频率乘总数;可估计总体;
(3)直接根据平均数的计算公式计算即可.
解:(1)∵跳绳次数不少于105次的同学占96%,即②③④⑤⑥组人数占96%,第①组频率为:1﹣96%=0.04.
∵第①、②两组频率之和为0.12,∴第②组频率为:0.12﹣0.04=0.08.
又∵第②组频数是12,∴这次跳绳测试共抽取学生人数为:12÷0.08=150(人).
∵②、③、④组的频数之比为4:17:15,∴12÷4=3(人),∴可算得第①~⑥组的人数分别为:①150×0.04=6(人),②4×3=12(人),③17×3=51(人),④15×3=45(人),⑥与②相同,为12人,⑤为150﹣6﹣12﹣51﹣45﹣12=24(人).
答:这次跳绳测试共抽取150名学生,各组的人数分别为6、12、51、45、24、12;
(2)第⑤、⑥两组的频率之和为=0.16+0.08=0.24,由于样本是随机抽取的,估计全年级有900×0.24=216人达到跳绳优秀.
答:估计全年级达到跳绳优秀的有216人.
(3)127(次).
答:这批学生1min跳绳次数的平均值为127次.
【点睛】本题考查了频率、频数的概念和对频数直方图的认识.要理解各组频率之和为1,各组频数之和等于总数.
班级_____________考号______________姓名_______________总分_________________
一、选择题(12小题,每题3分,共36分)
1.如图是某班一次数学测试成绩的频数直方图,则成绩在分范围内的学生共有
A.24人 B.10人 C.14人 D.29人
2.将“我爱北京天安门”用拼音可写成“WOAIBEIJINGTIANANMEN”,其中字母“I”出现的频率是( )
A.0.5 B.0.4 C.0.3 D.0.2
3.小敏统计了全班50名同学最喜欢的学科(每个同学只选一门学科).统计结果显示:最喜欢数学和科学的频数分别是13和10.最喜欢语文和英语的人数的频率分别是0.3和0.2,其余的同学最喜欢社会,则下列叙述错误的是( )
A.最喜欢语文的人数最多
B.最喜欢社会的人数最少
C.最喜欢数学的人数和最喜欢语文的人数之和超过总人数的一半
D.最喜欢科学的人数比最喜欢英语的人数要少
4.某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如图所示的统计图. 甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数的比为4∶17∶15,则本次测试共抽调的人数为( )
A.120 B.150 C.180 D.无法确定
5.已知20个数据如下:
25 21 29 30 24 25 29 28 27 23
27 26 22 24 28 26 25 23 25 27
对这些数据进行分析,其中24.5~26.5这一组的频率是( )
A.0.40 B.0.30 C.0.55 D.0.25
6.下表为某公司200名职员年龄的人数分配表,其中36~42岁及50~56岁的人数因污损而无法看出.若36~42岁及50~56岁职员人数的相对次数分别为a%、b%,则a+b之值为何?( )
年龄
22~28
29~35
36~42
43~49
50~56
57~63
次数
6
40
42
2
A.10 B.45 C.55 D.99
7.某次数学测验,抽取部分同学的成绩(得分为整数)整理制成频数分布直方图,如图所示.根据图示信息,下列描述不正确的是( )
A.共抽取了50人
B.90分以上的有12人
C.80分以上的所占的百分比是60%
D.60.5~70.5分这一分数段的频数是12
8.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:则通话时间不超过15min的频率为( )
通话时间x/min
0<x≤5
5<x≤10
10<x≤15
15<x≤20
频数(通话次数)
20
16
9
5
A.0.1 B.0.4 C.0.5 D.0.9
9.在某次人才交流会上,应聘人数和招聘人数分别居前5位的行业列表如下:
如果用同一行业应聘人数与招聘人数比值的大小来衡量该行业的就业情况,那么根据表中数据,对上述行业的就业情况判断正确的是( )
A.计算机行业好于其它行业 B.贸易行业好于化工行业
C.机械行业好于营销行业 D.建筑行业好于物流行业
10.列频数分布表考查50名学生年龄时,这些学生的年龄落在5个小组中,第一、二、三、五组的数据个数分别是1,9,15,5,则第四组的频数是( ).
A.10 B.9 C.15 D.20
11.某班学生在颁奖大会上得知该班获得奖励的情况如下表:
三好学生
优秀学生干部
优秀团员
市级
3
2
3
校级
18
6
12
已知该班共有28人获得奖励,其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
A.3项 B.4项 C.5项 D.6项
12.为了了解某地区八年级男生的身高情况,从其中一个学校选取容量为50的样本,50名男生的身高(单位:cm)分组情况如下表所示,则表中a,b的值分别是( )
分组
147.5~155.5
155.5~163.5
163.5~171.5
171.5~179.5
频数
10
18
a
频率
0.3
b
A.15,7 B.15,0.14 C.0.14,15 D.7,15
二、填空题(6小题,每题3分,共18分)
13.在一块试验田里抽取1000个小麦穗,考察它们的长度(单位:cm),从频率分布表中看到,样本数据落5.75cm~6.05cm之间的频率是0.36,于是可以估计,在这块土地里,长度在5.75cm~6.05cm之间的麦穗约占________
14.一次数学测试后,某班50名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、8,则第5组的频率是_____________.
15.有一个样本共有50个数据,分成若干组后,其中有一小组的频率是0.4,则该组的频数是_____.
16.一组数据,最大值与最小值的差为16,取组距为4,则组数为_____.
17.抽取某校学生一个容量为150的样本,测得学生身高后,得到身高频数分布直方图如图,已知该校有学生1500人,则可以估计出该校身高位于160 cm和165 cm之间的学生大约有_______人.
18.下表是某校八年级(8)班共50位同学身高情况的频数分布表,则表中的组距是7,估计极差至多是27.
组别(cm)
145.5~152.5
152.5~159.5
159.5~166.5
166.5~173.5
频数(人)
9
19
14
8
频率是0.28的这一小组的组中值是___.
三、解答题(8小题,共66分)
19.要了解中学生的身体发育情况,对某中学同龄的50名女学生的身高进行了测量,结果如下(单位:厘米):
165 158 160 166 157 161 152 163 161 167
169 162 155 157 162 163 156 167 159 171
150 153 156 167 165 164 163 164 161 161
148 160 155 165 155 158 159 153 156 156
164 162 156 162 157 162 165 151 159 157
列出样本的频率分布表.
20.统计某校七年级部分同学的立定跳远测试成绩,得到如图频数分布直方图(每组含前一个边界值,不含后一个边界值). 请根据右图,回答下列问题:
(1)参加测试的总人数是 ;数据分组的组距是 ;频数最大一组的组中值是 ;
(2)成绩在1.50m(含1.50m)以上的为合格,求这部分同学本次测试成绩的合格率.
21.某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg)
频数
4.0~4.5
2
4.5~5.0
a
5.0~5.5
3
5.5~6.0
1
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.
22.为了对某市区全民阅读状况进行调查和评估,有关部门随机抽取了部分市民进行每天阅读时间情况的调查,并根据调查结果制做了如下尚不完整的频数分布表(被调查者每天的阅读时间均在0﹣120分钟之内)
阅读时间x(分钟)
0≤x<30
30≤x<60
60≤x<90
90≤x≤120
频数
450
400
m
50
频率
0.45
0.4
0.1
n
(1)被调查的市民人数为多少,表格中,m,n为多少;
(2)补全频数分布直方图;
(3)某市区目前的常住人口约有118万人,请估计该市区每天阅读时间在60~120分钟的市民大约有多少万人?
23.某地区为了增强市民的法制观念,抽调了一部分市民进行了一次知识竞赛,竞赛成绩(得分数取整数)进行整理后分成五组,并绘制成频数分布直方图,请结合图提供的信息,解答下列问题:
(1)抽取了多少人参加竞赛?
(2)61~71这一分数段的频数和频率分别是多少?
(3)根据统计图,请你提出一个问题,并回答你所提出的问题.
24.南京某中学为了迎接世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:
请结合图表完成下列各题:
(1)求表中a的值:
(2)请把频数分布直方图补充完整:
(3)若测试成绩不低于90分的同学可以获得世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”?
25.某市第三中学组织学生参加生命安全知识网络测试.小明对七年级二班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图:
根据图表中的信息解答下列问题:
(1)七年级二班学生的人数为________,频数分布表中的值为________;
(2)已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上(含80分)为优秀,佔计该市本次测试成绩达到优秀的人数;
(3)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因。
26.某校九年级学生共900人,为了解这个年级学生的体能,从中随机抽取部分学生进行1min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理.下面是这四名同学提供的部分信息:甲:将全体测试数据分成6组绘成直方图(如图);乙:跳绳次数不少于105次的同学占96%;丙:第①、②两组频率之和为0.12,且第②组与第⑥组频数都是12;丁:第②、③、④组的频数之比为4∶17∶15.
根据这四名同学提供的材料,请解答如下问题:
(1)这次跳绳测试共抽取多少名学生?各组有多少人?
(2)如果跳绳次数不少于135次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为多少?
(3)以每组的组中值(每组的中点对应的数据)作为这组跳绳次数的代表,估计这批学生1min跳绳次数的平均值.
参考答案
1.【考点】频数分布直方图
【分析】根据直方图给出的数据,把成绩在分范围内的学生人数相加即可得出答案.
解:成绩在分范围内的学生共有:人, 故选:A.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
2.【考点】频率的计算
【分析】数出共20个字母,I出现了4次,用4÷20即可求出频率.
解:依题意4÷20=0.2,故选D.
【点睛】此题主要考察频率的计算.
3.【考点】频数和频
【分析】依据,可求出最喜欢语文和英语的人数,进而求出最喜欢社会的人数,然后逐个判断即可.
解:∵最喜欢语文和英语的人数的频率分别是0.3和0.2,总体为50,
∴喜欢语文的人数为0.3×50=15人,喜欢英语的人数为0.2×50=10人,则最喜欢社会的人数为50?13?10?15?10=2人,则最喜欢数学的人数和最喜欢语文的人数之和为13+15=28人,超过总人数的一半,故A、B、C正确.
故选D.
【点睛】这是一道考查频数和频率的题目,解题关键在于掌握频数和频率与总体的关系:,.
4.【考点】频数直方图
【分析】各小组频数之和等于数据总和,各小组的频率之和等于1;易知第二组的频率0.08;再由频数为12,得出总人数.
解:∵跳绳次数不少于100次的同学占96%,
∴第一组的频率为1-0.96=0.04,
∴第二组的频率为0.12-0.04=0.08,
故总人数为120.08=150(人),
故选B.
【点睛】此题主要考察频数直方图.
5.【考点】频率、频数
【分析】首先正确数出在24.5-26.5这组的数据的频数;再根据进行计算.
解:其中在24.5-26.5组的共有6个,
则24.5-26.5这组的频率是6÷20=0.30.
故选B.
【点睛】本题考查频率、频数的关系,难度不大,注意正确查出相关数据的人数及名单频数,根据的关系解答.
6.【考点】表格数据的读取
【分析】先求出36~42岁及50~56岁的职员人数和,再求出他们的占比.
解:由表知36~42岁及50~56岁的职员人数共有,
200﹣6﹣40﹣42﹣2=110人,
所以,a%+b%=×100%=55%,
所以a+b=55.
故选:C.
【点睛】此题主要考查表格数据的读取,解题的关键是先求出人数之和.
7.【考点】读频数分布直方图
【分析】根据表中提供的数据分别进行计算,即可找出描述不正确的选项.
解:A、抽样的学生共有:4+10+18+12+6=50人,故本选项正确,不符合题意;
B. 90分以上的有12人,故本选项正确,不符合题意;
C. 80分以上的所占的百分比是=60%;故本选项正确,不符合题意;
D. 60.5~70.5分这一分数段的频数是10,故本选项错误,符合题意;
故选D.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
8.【考点】频数分布表
【分析】用不超过15分钟的通话次数除以所有的通话次数即可求得通话时间不超过15分钟的频率.
解:∵不超过15分钟的通话次数为20+16+9=45次,通话总次数为20+16+9+5=50次, ∴通话时间不超过15min的频率为 =0.9, 故选:D.
【点睛】本题考查频数分布表的知识,解题关键是了解频率=频数÷样本容量,难度不大.
9.【考点】统计表
【分析】通过统计表可以得到应聘人数与招聘人数,进而通过计算应聘人数与招聘人数的比值大小来衡量该行业的就业情况,比值越小越容易就业,比值越大越不容易就业,通过计算即可求解.
解:计算机行业比值为1.84;机械行业比值为2.29;营销行业比值为1.50;建筑行业比值<≈0.86;化工行业比值<≈0.91;而物流行业比值>≈1.23,贸易行业的比值<≈0.90,
∴计算机行业比值不是最小的,因此不是最优的,故A错误;贸易行业与化工行业不确定大小,故B错误;机械行业比值大于营销行业比值,故营销行业优于机械行业,故C错误;建筑行业比值小于物流行业比值,故D正确. 故选:D.
【点睛】本题考查了统计部分的有关知识,解题关键是通过计算应聘人数与招聘人数的比值大小来衡量该行业的就业情况.
10.【考点】频数
【分析】由五个小组的频数总和等于50即可算出第四组的频数.
解:∵第一、二、三、五组的数据个数分别是1,9,15,5,
∴第四小组的频数是50﹣(1+9+15+5)=20.
故选:D.
【点睛】本题是对频数的考查,各小组频数之和等于数据总和.
11.【考点】频数分布表
【分析】求得除获两项奖励的人数,以及这些人获得的奖的项数即可作出判断.
解:各项频数的和是:2+3+3+15+9+12=44; 获得两项奖励的有13人,则奖数是2×13=26; 44-26=18, 28-13=15, 则获奖最多的一名学生的获奖项数是:1+(18-15)=4. 故答案是:4.
【点睛】本题考查了频数分布表,分清各项数据的关系是本题的解题关键.
12.【考点】频率分布表
【分析】根据样本容量为50,由频率与频数的关系可求出a=15,根据前两组的频数求出学生身高为171.5~179.5的频数,再利用频率与频数的关系即可求出b=0.14.
解:∵样本容量为50,
∴a=50×0.3=15;
∴学生身高为171.5~179.5的频数为:50-10-18-15=7,
∴b=7÷50=0.14.
故选B.
【点睛】本题考点是频率分布表,考查对频率分布表结构的认识,以及其中数据的意义.是统计中的基本题型.
13.【考点】频率可以估计事件
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近.
解:∵抽取1000个麦穗考查它的长度落在5.75~6.05之间的频率为0.36,
∴这块田里长度为5.75~6.05cm之间的麦约占36%.
故本题答案为:36%.
【点睛】本题考查了样本估计总体,利用了用大量试验得到的频率可以估计事件的概率.
14.【考点】频率,频数之间的关系
【分析】根据第1~4组的频数,求出第5组的频数,即可确定出其频率.
解:根据题意得:50?(12+10+6+8)=50?36=14,
则第5组的频率为14÷50=0.28,
故答案为:0.28.
【点睛】考查频率,频数之间的关系,掌握它们之间的关系式是解题的关键.
15.【考点】频数与频率
【分析】由公式:频率=,得:频数=总数据×频率,即可求出答案.
解:由题意得:
该组的频数为:50×0.4=20.
故答案为:20.
【点睛】本题考查了频数与频率,难度一般,能够灵活运用频率=这一公式是解决本题的关键.
16.【考点】组数
【分析】在样本数据中最大值与最小值的差为16,已知组距为4,那么由于16÷4=4,且要求包含两个端点在内;故可以分成5组.
解:∵16÷4=4,
∴组数为5,
故答案为:5.
【点睛】本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
17.【考点】频数分布直方图
【分析】根据频率直方图的意义,由用样本估计总体的方法可得样本中160~165的人数,进而可得其频率;计算可得1500名学生中身高位于160cm至165cm之间的人数
解:由题意可知:150名样本中160~165的人数为30人,则其频率为,
则1500名学生中身高位于160cm至165cm之间大约有1500×=300人.
故答案为:300.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;同时本题很好的考查了用样本来估计总体的数学思想.
18.【考点】频率与频数
【分析】先求出频率是0.28的一组的频数,再求出其组中值即可.
解:频率是0.28的一组的频数=50×0.28=14人,
∴这一组是159.5﹣166.5组,
∴组中值为=163.
故本题答案为:163.
【点睛】此题主要考查频率与频数的关系,解题的关键是根据频率求出频数.
19.【考点】列频率分布表
【分析】据题意,计算极差,确定组距与组数,列频率分布表,
解:①计算极差为:171-148=23, ②确定组距与组数:以4为组距,23≈6,可以分为6组; ③列频率分布表,如下;
小组
频数
频率
(147.5,151.5)
3
0.06
(151.5,155.5)
6
0.12
(155.5,159.5)
14
0.28
(159.5,163.5)
14
0.28
(163.5,167.5)
11
0.22
(167.5,171.5)
2
0.04
总计
50
1.00
【点睛】本题考查了列频率分布表,是基础题目.熟练掌握画频率分布直方图的基本步骤是解题的关键。
20.【考点】条形统计图运用
【分析】根据条形统计图即可得到每一组的人数,根据每组的组中值即可确定组距,据此即可作出判断.
解:(1)4+6+14+10+6=40人 1.60-1.40=0.2m 1.80m ;
(2)(6+14+10+6)÷40=90%.
【点睛】本题考查的是条形统计图运用,解题关键是读懂统计图,从统计图中得到必要的信息.
21.【考点】条形统计图运用
【分析】根据条形统计图的应用来解答即可.
解:(1)观察频数分布直方图可得出a=4;
(2)每组含前一个边界值,不含后一个边界值,
∵2×4.5+4×5+3×5.5+1×6=51.5kg,
∴总质量小于51.5kg,∵51.5×0.8=41.2元<50元,
∴该年级这周的可回收垃圾被回收后所得金额不能达到50元.
【点睛】此题主要考察条形统计图的应用.
22.【考点】频数分布直方图
【分析】(1)根据0≤x<30的频数和频率先求出总人数,用总人数乘以60≤x<90的频率求出m,用90≤x≤120的频数除以总人数求出n;
(2)根据(1)求出的总人数,补全统计图即可;
(3)用常住人口数乘以阅读时间在60~120 分钟的人数的频率即可得出答案.
解:(1)根据题意得:被调查的市民人数为=1000(人),
m=1000×0.1=100,
n==0.05;
(2)根据(1)补图如下:
(3)根据题意得:118×(0.1+0.05)=17.7(万人)
估计该市区每天阅读时间在 60~120分钟的市民大约有17.7万人.
故答案为:(1)1000,100,0.05;(2)根据(1)补图见解析;(3)估计该市区每天阅读时间在 60~120分钟的市民大约有17.7万人.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
23.【考点】频数直方图的应用
【分析】(1)在直方图中找到各组的人数再相加即得总人数;(2)根据直方图找到61~71这一分数段的频数为12,再求出频率即可.(3)根据直方图得出成绩在80.5分以上有15人,若成绩在80.5分以上的同学获奖,则可求出获奖率.
解:(1)3+6+9+12+18=48(人),即抽取了48人参加竞赛.
(2)61~71这一分数段的频数为12,频率为=.
(3)答案不唯一.如果成绩在80.5分以上的同学获奖,那么此知识竞赛活动参赛市民的获奖率是多少?解答:≈0.31=31%.
【点睛】此题主要考察频数直方图的应用.
24.【考点】频数分布直方图
【分析】(1)用随机抽查的总数减去第1组、第2组、第4组、第5组的频数即可求出a的值;
(2)根据(1)求出的a的值和第4组的人数即可补全统计图;
(3)用全年级的总人数乘以成绩不低于90分的同学所占的百分比即可得出答案.
解:(1)a=100﹣(8+16+32+20)=24;
(2)根据题意补图如下:
(3)根据题意得:
600× 20% =120(人),
答:该校九年级有 120 人可以获得“乒宝”.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
25.【考点】频数分布表和扇形统计图
【分析】(1)根据数据总数=代入计算,求出七年级2班学生的人数; (2)先计算优秀的百分比,再与80000相乘即可; (3)取的样本不足以代表全市总中学的总体情况.
解:(1)17÷34%=50(人),a=24%×50=12, 答:九年级2班学生的人数为50人;
(2)E:14÷50=28%, (28%+24%)×80000=52×800=41600(人), 答:估计该市本次测试成绩达到优秀的人数为41600人; (3)全市参加本次测试的中学生中,成绩达到优秀有56?320人;而样本中估计该市本次测试成绩达到优秀的人数为41600人,原因是:小明对第三中学九年2班全体学生的测试成绩取的样本不足以代表全市总中学的总体情况,所以会出现较大偏差.
【点睛】本题考查了数据的收集与整理,根据频数分布表和扇形统计图可以将大量数据分类,结果清晰,一目了然地表达出来,熟练掌握公式是做好本题的关键:数据总数=,各组频数和=总数据.
26.【考点】频率、频数的概念,频数直方图
【分析】(1)由直方图中,各组频率之和为1,可求出②③组的频率,再根据②③组的频数结合频数与频率的关系可求得总数;
(2)从图中可以看出,第⑤⑥组的频数在135以上,故这两组优秀,所以用它们的频率乘总数;可估计总体;
(3)直接根据平均数的计算公式计算即可.
解:(1)∵跳绳次数不少于105次的同学占96%,即②③④⑤⑥组人数占96%,第①组频率为:1﹣96%=0.04.
∵第①、②两组频率之和为0.12,∴第②组频率为:0.12﹣0.04=0.08.
又∵第②组频数是12,∴这次跳绳测试共抽取学生人数为:12÷0.08=150(人).
∵②、③、④组的频数之比为4:17:15,∴12÷4=3(人),∴可算得第①~⑥组的人数分别为:①150×0.04=6(人),②4×3=12(人),③17×3=51(人),④15×3=45(人),⑥与②相同,为12人,⑤为150﹣6﹣12﹣51﹣45﹣12=24(人).
答:这次跳绳测试共抽取150名学生,各组的人数分别为6、12、51、45、24、12;
(2)第⑤、⑥两组的频率之和为=0.16+0.08=0.24,由于样本是随机抽取的,估计全年级有900×0.24=216人达到跳绳优秀.
答:估计全年级达到跳绳优秀的有216人.
(3)127(次).
答:这批学生1min跳绳次数的平均值为127次.
【点睛】本题考查了频率、频数的概念和对频数直方图的认识.要理解各组频率之和为1,各组频数之和等于总数.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
