苏科版数学九下6.7《用相似三角形解决问题(第2课时)》课件 共20张PPT
文档属性
| 名称 | 苏科版数学九下6.7《用相似三角形解决问题(第2课时)》课件 共20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 373.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-15 09:06:46 | ||
图片预览



文档简介
课件20张PPT。6.7 相似三角形的应用(2)——虚幻的影子,真实的信息情景创设白天,走在太阳光下,你走,影子也在走,影子的长度会改变吗?为什么?(短时间内时间误差忽略不记)
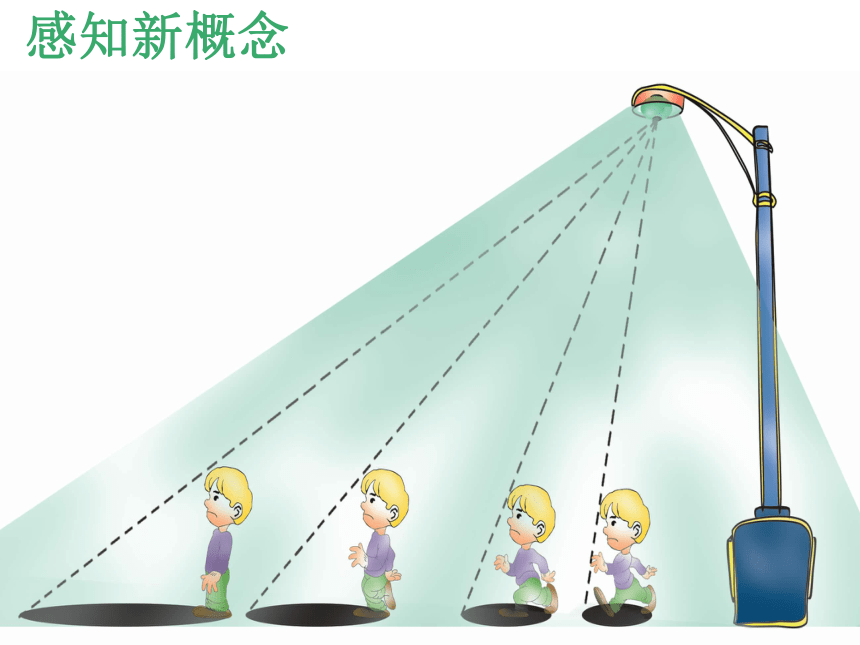
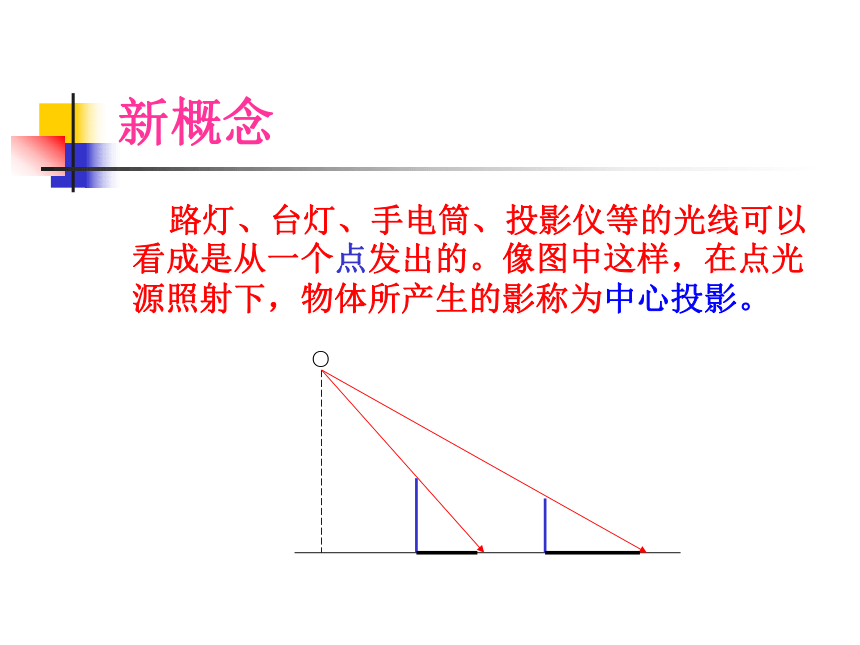
夜晚,走在路灯下,你走,影子也在走,影子的长度会改变吗?感知新概念新概念 路灯、台灯、手电筒、投影仪等的光线可以看成是从一个点发出的。像图中这样,在点光源照射下,物体所产生的影称为中心投影。
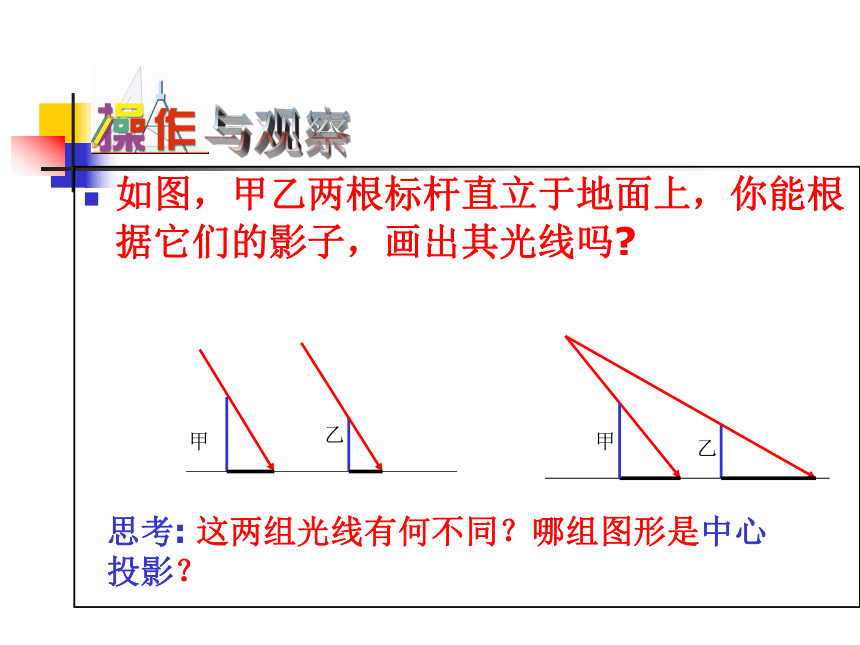
○ 如图,甲乙两根标杆直立于地面上,你能根据它们的影子,画出其光线吗?
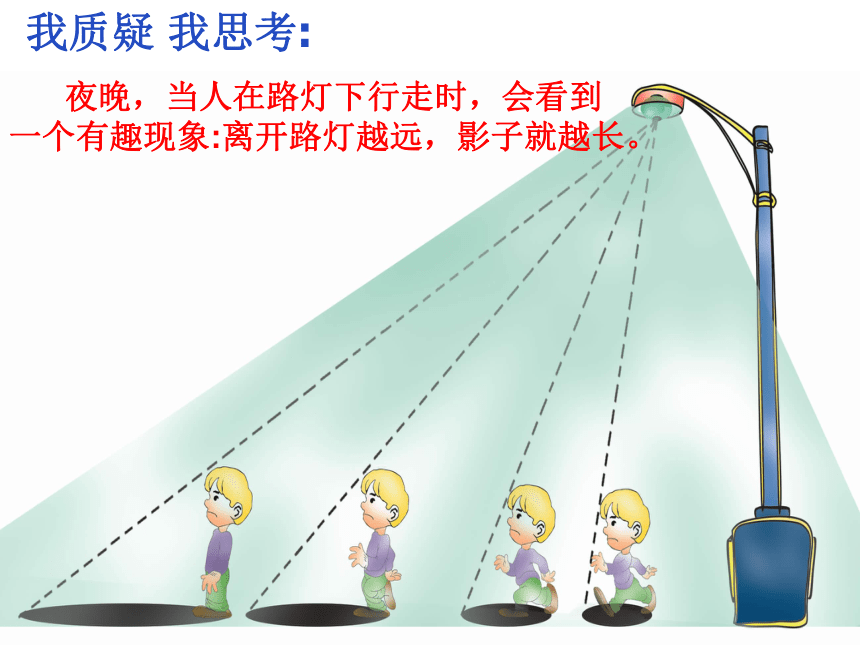
甲乙乙甲 思考: 这两组光线有何不同?哪组图形是中心投影? 与观察 夜晚,当人在路灯下行走时,会看到一个有趣现象:离开路灯越远,影子就越长。我质疑 我思考:探索与发现
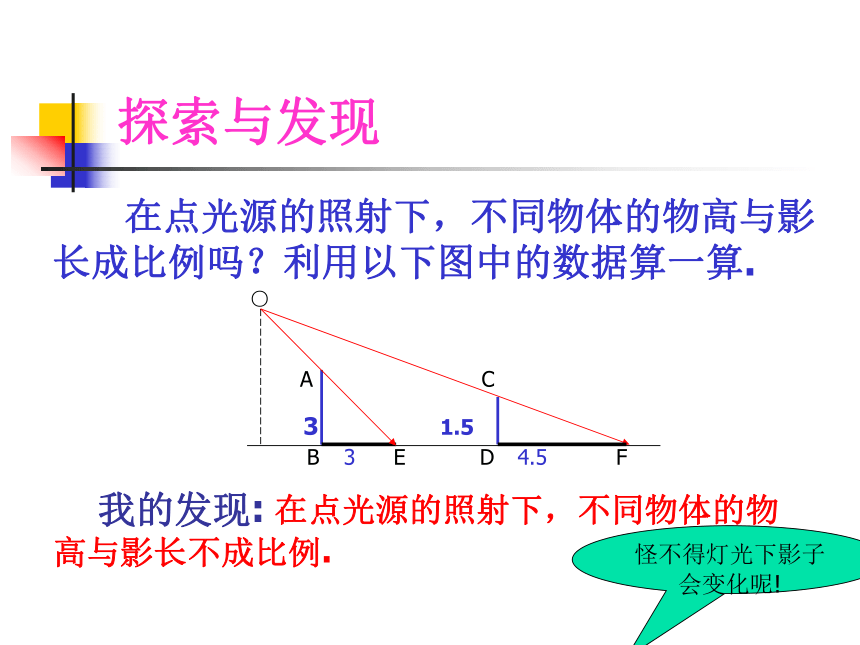
我的发现: 在点光源的照射下,不同物体的物高与影长不成比例.
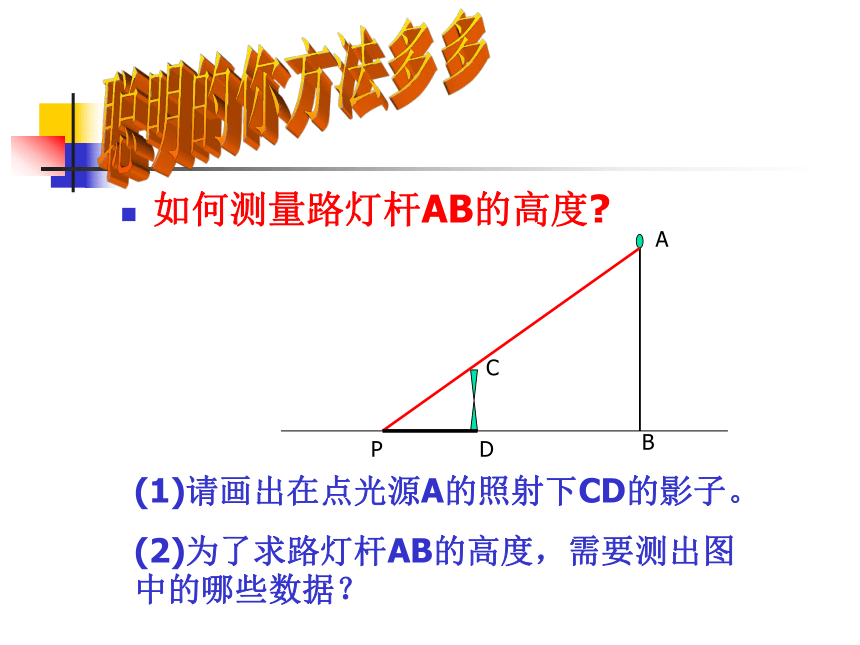
○ 在点光源的照射下,不同物体的物高与影长成比例吗?利用以下图中的数据算一算.怪不得灯光下影子会变化呢!如何测量路灯杆AB的高度?(1)请画出在点光源A的照射下CD的影子。
(2)为了求路灯杆AB的高度,需要测出图中的哪些数据?·BCDPA聪明的你方法多多试一试
如图,某同学的身高CD=1.6m,他从路灯底部的点B直行4m到点D,此时其影长PD=2m.求路灯杆AB的高度. C D PAB(小方案,大思想)八仙过海 若小明与路灯底部之间有障碍物,不能测出他与路灯底部B之间的距离,利用现有的图形能测出路灯AB的高度吗?ABCDF1.63? 河对岸有一路灯杆AB,在灯光下,小明在点D处测得自己的影长DF= 3 m,沿BD方向到达点F处再测得自己的影长FG= 4 m,如果小明的身高为1.6 m,求路灯杆AB的高度。ABDCEFG 开动脑筋喽!341.61.6? 把握条件,发现或构造相似三角形
利用相似三角形的性质,得到与未知,已知相关的比例式
解由比例式构建的方程或方程组,求出未知量.利用相似三角形解实际问题的思路:解法点拨:解法点拨我的方案 我解答 (A组).为了测量河对岸路灯杆AB的高度,在灯光下,小明在点D处测得自己的影长DF= 3 m,然后他沿BD方向远离路灯的方向走了4 m,到达点H处再测得自己的影长HG= 4 m,如果小明的身高为1.6 m,求路灯杆AB的高度。(只列不解)351.6GFE1.6ABCD1.61.6H我的方案 我解答(B组)花丛中有一路灯杆AB,在灯光下,小明在D点处的影长DE=3 m,小亮恰巧在点E处,且小亮的影长EG=3 m。如果小明的身高为1.6m,小亮的身高为1.2m ,求路灯杆AB的高度 (只列不解) 。
ABDEGCF31.61.23甲乙拓展与提高 王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后的影子顶部刚好触到AC的底部,当他向前再步行12 m到达Q点时,发现身前的影子的顶端接触到路灯BD的底部。已知王华身高为1.6 m,两个路灯的高度都是9.6 m。
(1) 求两个路灯之间的距离。
(2) 当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?(先画完图形,再解答.)CABPQDEMNF 平行投影 中心投影
异图示性质同啊哈,还是相似三角形的应用呀!找到相似三角形,列出可求出未知量的比例式再解就OK了.在平行光线的照射下,不同物体的物高和影长成比例.
(不具备前者性质,即在点光源的照射下,不同物体的物高与影长不成比例.) 一般的,它们都能利用相似三角形的知识解决问题.比一比,更明白通过这节课的学习,你有哪些收获?请你从知识,学法等方面谈一谈。课堂总结 (1)解决实际问题时(如测高、测距),一般有以下 步骤:审题 ;构建图形,找相似三角形;利用相似三角形形性质解决问题(2)猜想、验证与比较是常用的数学方法(3)方程或方程组是常用的数学工具,注意在解决问时建立其模型 (1)花丛中有一路灯杆AB,在灯光下,小明在D点处的影长DE=3 m,沿BD方向行走到达G点,DG=5 m,这时小明的影长GH=5 m。如果小明的身高为1.7 m,求路灯杆AB的高度。作业布置:作业布置 (2)已知窗框的影子DE的E点到窗下墙脚距离CE=3.9 m。窗口底边离地面的距离BC=1.2 m。试求窗口的高度(即AB的值)
谢谢您的指导
夜晚,走在路灯下,你走,影子也在走,影子的长度会改变吗?感知新概念新概念 路灯、台灯、手电筒、投影仪等的光线可以看成是从一个点发出的。像图中这样,在点光源照射下,物体所产生的影称为中心投影。
○ 如图,甲乙两根标杆直立于地面上,你能根据它们的影子,画出其光线吗?
甲乙乙甲 思考: 这两组光线有何不同?哪组图形是中心投影? 与观察 夜晚,当人在路灯下行走时,会看到一个有趣现象:离开路灯越远,影子就越长。我质疑 我思考:探索与发现
我的发现: 在点光源的照射下,不同物体的物高与影长不成比例.
○ 在点光源的照射下,不同物体的物高与影长成比例吗?利用以下图中的数据算一算.怪不得灯光下影子会变化呢!如何测量路灯杆AB的高度?(1)请画出在点光源A的照射下CD的影子。
(2)为了求路灯杆AB的高度,需要测出图中的哪些数据?·BCDPA聪明的你方法多多试一试
如图,某同学的身高CD=1.6m,他从路灯底部的点B直行4m到点D,此时其影长PD=2m.求路灯杆AB的高度. C D PAB(小方案,大思想)八仙过海 若小明与路灯底部之间有障碍物,不能测出他与路灯底部B之间的距离,利用现有的图形能测出路灯AB的高度吗?ABCDF1.63? 河对岸有一路灯杆AB,在灯光下,小明在点D处测得自己的影长DF= 3 m,沿BD方向到达点F处再测得自己的影长FG= 4 m,如果小明的身高为1.6 m,求路灯杆AB的高度。ABDCEFG 开动脑筋喽!341.61.6? 把握条件,发现或构造相似三角形
利用相似三角形的性质,得到与未知,已知相关的比例式
解由比例式构建的方程或方程组,求出未知量.利用相似三角形解实际问题的思路:解法点拨:解法点拨我的方案 我解答 (A组).为了测量河对岸路灯杆AB的高度,在灯光下,小明在点D处测得自己的影长DF= 3 m,然后他沿BD方向远离路灯的方向走了4 m,到达点H处再测得自己的影长HG= 4 m,如果小明的身高为1.6 m,求路灯杆AB的高度。(只列不解)351.6GFE1.6ABCD1.61.6H我的方案 我解答(B组)花丛中有一路灯杆AB,在灯光下,小明在D点处的影长DE=3 m,小亮恰巧在点E处,且小亮的影长EG=3 m。如果小明的身高为1.6m,小亮的身高为1.2m ,求路灯杆AB的高度 (只列不解) 。
ABDEGCF31.61.23甲乙拓展与提高 王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后的影子顶部刚好触到AC的底部,当他向前再步行12 m到达Q点时,发现身前的影子的顶端接触到路灯BD的底部。已知王华身高为1.6 m,两个路灯的高度都是9.6 m。
(1) 求两个路灯之间的距离。
(2) 当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?(先画完图形,再解答.)CABPQDEMNF 平行投影 中心投影
异图示性质同啊哈,还是相似三角形的应用呀!找到相似三角形,列出可求出未知量的比例式再解就OK了.在平行光线的照射下,不同物体的物高和影长成比例.
(不具备前者性质,即在点光源的照射下,不同物体的物高与影长不成比例.) 一般的,它们都能利用相似三角形的知识解决问题.比一比,更明白通过这节课的学习,你有哪些收获?请你从知识,学法等方面谈一谈。课堂总结 (1)解决实际问题时(如测高、测距),一般有以下 步骤:审题 ;构建图形,找相似三角形;利用相似三角形形性质解决问题(2)猜想、验证与比较是常用的数学方法(3)方程或方程组是常用的数学工具,注意在解决问时建立其模型 (1)花丛中有一路灯杆AB,在灯光下,小明在D点处的影长DE=3 m,沿BD方向行走到达G点,DG=5 m,这时小明的影长GH=5 m。如果小明的身高为1.7 m,求路灯杆AB的高度。作业布置:作业布置 (2)已知窗框的影子DE的E点到窗下墙脚距离CE=3.9 m。窗口底边离地面的距离BC=1.2 m。试求窗口的高度(即AB的值)
谢谢您的指导
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
