人教版数学七年级下册8.2 消元——二元一次方程组的解法(43张PPT)
文档属性
| 名称 | 人教版数学七年级下册8.2 消元——二元一次方程组的解法(43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-14 00:00:00 | ||
图片预览








文档简介
篮球联赛中,每场都要分出胜负,每队胜一场得2分,负一场得1分,某队为了争取较好的名次,想在全部的22场比赛中得到40分,那么这个队胜负应该分别是多少?
解法二:
设胜x场,则负(22-x)场,则有
2x+(22-x)=40③
解得 x=18,y=4.
解法一和解法二中的方程式有什么联系吗?
方程式①x+y=22写成y=22-x,代入方程式②中,可以得到方程式③.
1.熟练地解二元一次方程组;
2.了解消元的思想方法,设法消去方程中的一个未知数,把“二元”变成“一元”;
3.灵活运用代入消元法、加减消元法解方程组;
4.会用加减法求未知数系数相等或互为相反数的二元一次方程组的解.
知识与能力
通过探求二元一次方程组的解法,经历用加减法把“二元”化为“一元”的过程,体会消元的思想,以及把“未知”转化为“已知”,把复杂问题转化为简单问题的化归思想.
过程与方法
情感态度与价值观
1.通过研究解决问题的方法,培养合作交流意识与探究精神;
2.体会代入消元法和化未知为已知的数学思想.
二元一次方程组的解法——代入消元法和加减消元法,以及列出二元一次方程组解简单的实际问题.
二元一次方程的解的不确定性;二元一次方程组解的意义;列出二元一次方程组解简单的实际问题.
重点
难点
消元思想
消去二元一次方程组中的一个未知数,把它转化为一元一次方程进行求解,这种将未知数的个数由多化少、逐一解决的思想,叫消元思想.
知识要点
把二元一次方程组中一个方程的未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法.
8.2.1 代入消元法
例1 用代入法解方程组
1.??选取一个方程,将它写成用一个未知数表示另一个未知数,记作方程③. ? ? 2.把③代人另一个方程,得一元一次方程. ? ? 3.解这个一元一次方程,得一个未知数的值. ? ? 4.把这个未知数的值代人③,求出另一个未知数值,从而得到方程组的解.
代入消元法解二元一次方程组的过程:
知识要点
二元一次方程组
一元一次方程
一元一次方程的解
二元一次方程组的解
代入消元法
“化多为少、由繁至简、各个击破、逐一解决”的转化的数学思想.
转化
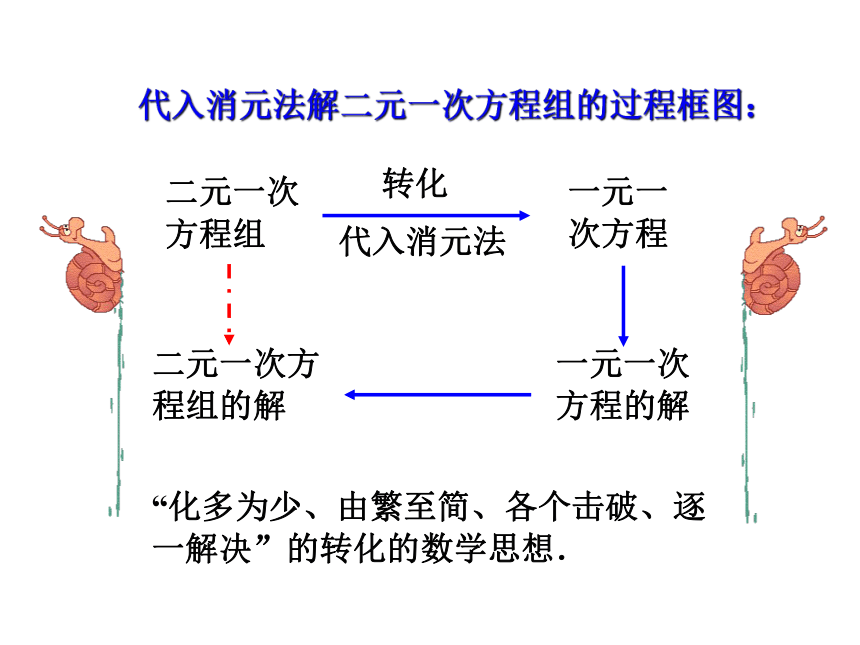
代入消元法解二元一次方程组的过程框图:
例3 两个完全相同的纸杯中盛有相同重量的水,现将第一个纸杯中的若干重量的水倒入第二个纸杯中,称得第一个纸杯重50克,第二个纸杯重90克(纸杯本身的重量忽略不计),问原来纸杯中各盛有多少克水?从第一个纸杯中倒了多少克水到第二个纸杯中?
解:设原来纸杯中盛有x克水,从第一个纸杯中倒入第二个纸杯中的水为y克,根据题意,得
由①,得 x=y+50. ③
把③代入②,得 y+50+y=90.
解这个方程,得 y=20.
把y=20代入③,得 x=70.
所以这个方程组的解是
答:原来纸杯中盛有70克水,从第一个纸杯中倒入第二个纸杯中的水为20克.
①+②得:(x-y)+(x+y)=50+90,
则有 2x=50+90 所以 x=70
或者:
②-①得 :(x+y) -(x-y)=90-50,
则有 2y=40 所以 y=20
上述方程的另一种解法是:
8.2.2 加减消元法
两个二元一次方程中同一未知数的系数相反或相等时,把两个方程两边分别相加(或相减)消去一个未知数,把二元一次方程组转化为一元一次方程,这种方法叫做加减消元法,简称加减法.
解:
① -②,得
9y = -18.
y= - 2.
把 y = - 2 代入 ① , 得
3x + 5 × ( - 2 ) = 5
解得
x = 5
所以这个方程组的解是
例4 用加减法解方程组
解这个方程得,
解:
① + ②,得
7x = 14
x = 2
把 x = 2 代入①,得
3 ×2 + 7y = 27
6 + 7y =27
y= 3
所以这个原方程组的解是
例6 用加减法解方程组
解:①×2,得
8x+10y=46 ③
②×5,得
25x-10y=20 ④
③+④,得 33x=66 x=2
把x=2代入②,得 5×2-2y=4, y=3
解:原方程组变形为
①-②,得:2y=2 y=1
把y=1代入①,得x=2
解:由①×6,得
3x+2y=9 ③
由②×15,得
5x-3y=15 ④
例8 用加减法解方程组
⑤+⑥,得 19x= 57 x=3
把x= 3代入③,得
③④组成一个新的方程组:
③×3,得 9x+6y=27 ⑤
④×2,得 10x-6y=30 ⑥
3×3+2y=9
y=0
当方程组中同一未知数的系数的绝对值不相等时,必须用等式性质来改变方程组中方程的形式,得到与原方程组同解的且某未知数系数的绝对值相等的新的方程组,从而为加减消元法解方程组创造条件.
主要步骤:
基本思路:
写解
求解
加减
二元变一元
加减消元:
消去一个元
求出两个未知数的值
写出方程组的解
加减消元法解方程组基本思路和主要步骤:
变形
同一个未知数的系数相同或互为相反数
解:①+②得(3k+6)y=0
即(2+k)y=0
(1)当k≠-2时,y=0
(2)当k=-2时,则k+2=0,(2+k)y=0恒成立
原方程组有无数组解.
例11 已知4|5x+3y-23| +5(x+4y-8)2 = 0 ,求x-y的值.
解:由题知,
解这个方程组,得
所以 x-y=4-1=3
例12 已知4x3a+b-3 +3y2a-b=2,是关于x、y的二元一次方程,试求a、b的值.
解:根据题意:得
解,得
解:由已知得
解得
把x=4z,y=2z代入所求代数式,解得
例13 当x = 2与x = -3时,代数式2x2+ax-b的值都是9,求a, b 的值.
解:把x=2,x=-3代入2x2+ax-b,得
即
解,得
解:若方程组的解互为相反数,则有y=-x,将y=-x代入原方程组,得
解,得
当a=3时,原方程组中的解互为相反数,
即
例15 m , n 为何值时,5x4m-ny3m+2n与3x5y6m是同类项.
解:根据同类项的定义,有
解,得
1.代入消元法解二元一次方程组
对于用代入法解未知数系数的绝对值不是1的二元一次方程组,解题时应选择未知数的系数绝对值比较小的一个方程进行变形,这样运算简便.
用加减法解二元一次方程组的思想:“二元”消元转化为“一元”.条件:某一未知数系数绝对值相等.
2.用加减消元法解二元一次方程组
2.若(x-2y-3)2+(2x-y-3)2=0, 则x、y的
值是x=___,y=______.
1
-1
3.已知│x+y-5│+(2x-3y+10)2=0,则
x=____,y=____.
1
4
x=2,y=3
5.已知(3m+2n-16)2与|3m-n-1|互为相反数,
则m+2n=_______.
12
6.若方程 (a2-9)x2+(2-4a)x+(a+4)y+
3a-5=0 是二元一次方程,则a的值为__.
±3
7.已知5a3xb2x-y和-9a8-yb7是同类项,则2xy=____.
-6
2
3
4
2
8
1
2
2
4.设买甲种票x张、买乙种票y张,
5.
6.设到花果山的有x人、到云水洞的有y人.
7.设甲、乙两人的平均速度分别为x千米/
时和y千米/时.
8.设每大盒装x瓶、每小盒装y瓶.
9.设长为xcm、宽为ycm.
解法二:
设胜x场,则负(22-x)场,则有
2x+(22-x)=40③
解得 x=18,y=4.
解法一和解法二中的方程式有什么联系吗?
方程式①x+y=22写成y=22-x,代入方程式②中,可以得到方程式③.
1.熟练地解二元一次方程组;
2.了解消元的思想方法,设法消去方程中的一个未知数,把“二元”变成“一元”;
3.灵活运用代入消元法、加减消元法解方程组;
4.会用加减法求未知数系数相等或互为相反数的二元一次方程组的解.
知识与能力
通过探求二元一次方程组的解法,经历用加减法把“二元”化为“一元”的过程,体会消元的思想,以及把“未知”转化为“已知”,把复杂问题转化为简单问题的化归思想.
过程与方法
情感态度与价值观
1.通过研究解决问题的方法,培养合作交流意识与探究精神;
2.体会代入消元法和化未知为已知的数学思想.
二元一次方程组的解法——代入消元法和加减消元法,以及列出二元一次方程组解简单的实际问题.
二元一次方程的解的不确定性;二元一次方程组解的意义;列出二元一次方程组解简单的实际问题.
重点
难点
消元思想
消去二元一次方程组中的一个未知数,把它转化为一元一次方程进行求解,这种将未知数的个数由多化少、逐一解决的思想,叫消元思想.
知识要点
把二元一次方程组中一个方程的未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法.
8.2.1 代入消元法
例1 用代入法解方程组
1.??选取一个方程,将它写成用一个未知数表示另一个未知数,记作方程③. ? ? 2.把③代人另一个方程,得一元一次方程. ? ? 3.解这个一元一次方程,得一个未知数的值. ? ? 4.把这个未知数的值代人③,求出另一个未知数值,从而得到方程组的解.
代入消元法解二元一次方程组的过程:
知识要点
二元一次方程组
一元一次方程
一元一次方程的解
二元一次方程组的解
代入消元法
“化多为少、由繁至简、各个击破、逐一解决”的转化的数学思想.
转化
代入消元法解二元一次方程组的过程框图:
例3 两个完全相同的纸杯中盛有相同重量的水,现将第一个纸杯中的若干重量的水倒入第二个纸杯中,称得第一个纸杯重50克,第二个纸杯重90克(纸杯本身的重量忽略不计),问原来纸杯中各盛有多少克水?从第一个纸杯中倒了多少克水到第二个纸杯中?
解:设原来纸杯中盛有x克水,从第一个纸杯中倒入第二个纸杯中的水为y克,根据题意,得
由①,得 x=y+50. ③
把③代入②,得 y+50+y=90.
解这个方程,得 y=20.
把y=20代入③,得 x=70.
所以这个方程组的解是
答:原来纸杯中盛有70克水,从第一个纸杯中倒入第二个纸杯中的水为20克.
①+②得:(x-y)+(x+y)=50+90,
则有 2x=50+90 所以 x=70
或者:
②-①得 :(x+y) -(x-y)=90-50,
则有 2y=40 所以 y=20
上述方程的另一种解法是:
8.2.2 加减消元法
两个二元一次方程中同一未知数的系数相反或相等时,把两个方程两边分别相加(或相减)消去一个未知数,把二元一次方程组转化为一元一次方程,这种方法叫做加减消元法,简称加减法.
解:
① -②,得
9y = -18.
y= - 2.
把 y = - 2 代入 ① , 得
3x + 5 × ( - 2 ) = 5
解得
x = 5
所以这个方程组的解是
例4 用加减法解方程组
解这个方程得,
解:
① + ②,得
7x = 14
x = 2
把 x = 2 代入①,得
3 ×2 + 7y = 27
6 + 7y =27
y= 3
所以这个原方程组的解是
例6 用加减法解方程组
解:①×2,得
8x+10y=46 ③
②×5,得
25x-10y=20 ④
③+④,得 33x=66 x=2
把x=2代入②,得 5×2-2y=4, y=3
解:原方程组变形为
①-②,得:2y=2 y=1
把y=1代入①,得x=2
解:由①×6,得
3x+2y=9 ③
由②×15,得
5x-3y=15 ④
例8 用加减法解方程组
⑤+⑥,得 19x= 57 x=3
把x= 3代入③,得
③④组成一个新的方程组:
③×3,得 9x+6y=27 ⑤
④×2,得 10x-6y=30 ⑥
3×3+2y=9
y=0
当方程组中同一未知数的系数的绝对值不相等时,必须用等式性质来改变方程组中方程的形式,得到与原方程组同解的且某未知数系数的绝对值相等的新的方程组,从而为加减消元法解方程组创造条件.
主要步骤:
基本思路:
写解
求解
加减
二元变一元
加减消元:
消去一个元
求出两个未知数的值
写出方程组的解
加减消元法解方程组基本思路和主要步骤:
变形
同一个未知数的系数相同或互为相反数
解:①+②得(3k+6)y=0
即(2+k)y=0
(1)当k≠-2时,y=0
(2)当k=-2时,则k+2=0,(2+k)y=0恒成立
原方程组有无数组解.
例11 已知4|5x+3y-23| +5(x+4y-8)2 = 0 ,求x-y的值.
解:由题知,
解这个方程组,得
所以 x-y=4-1=3
例12 已知4x3a+b-3 +3y2a-b=2,是关于x、y的二元一次方程,试求a、b的值.
解:根据题意:得
解,得
解:由已知得
解得
把x=4z,y=2z代入所求代数式,解得
例13 当x = 2与x = -3时,代数式2x2+ax-b的值都是9,求a, b 的值.
解:把x=2,x=-3代入2x2+ax-b,得
即
解,得
解:若方程组的解互为相反数,则有y=-x,将y=-x代入原方程组,得
解,得
当a=3时,原方程组中的解互为相反数,
即
例15 m , n 为何值时,5x4m-ny3m+2n与3x5y6m是同类项.
解:根据同类项的定义,有
解,得
1.代入消元法解二元一次方程组
对于用代入法解未知数系数的绝对值不是1的二元一次方程组,解题时应选择未知数的系数绝对值比较小的一个方程进行变形,这样运算简便.
用加减法解二元一次方程组的思想:“二元”消元转化为“一元”.条件:某一未知数系数绝对值相等.
2.用加减消元法解二元一次方程组
2.若(x-2y-3)2+(2x-y-3)2=0, 则x、y的
值是x=___,y=______.
1
-1
3.已知│x+y-5│+(2x-3y+10)2=0,则
x=____,y=____.
1
4
x=2,y=3
5.已知(3m+2n-16)2与|3m-n-1|互为相反数,
则m+2n=_______.
12
6.若方程 (a2-9)x2+(2-4a)x+(a+4)y+
3a-5=0 是二元一次方程,则a的值为__.
±3
7.已知5a3xb2x-y和-9a8-yb7是同类项,则2xy=____.
-6
2
3
4
2
8
1
2
2
4.设买甲种票x张、买乙种票y张,
5.
6.设到花果山的有x人、到云水洞的有y人.
7.设甲、乙两人的平均速度分别为x千米/
时和y千米/时.
8.设每大盒装x瓶、每小盒装y瓶.
9.设长为xcm、宽为ycm.
