2019人教A版数学必修四课件:第二章 平面向量 2.3.2 平面向量的正交分解及坐标表示 2.3.3 平面向量的坐标运算(情境互动课型)(39张PPT)
文档属性
| 名称 | 2019人教A版数学必修四课件:第二章 平面向量 2.3.2 平面向量的正交分解及坐标表示 2.3.3 平面向量的坐标运算(情境互动课型)(39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-14 18:18:28 | ||
图片预览






文档简介
课件39张PPT。2.3.2 平面向量的正交分解及坐标表示
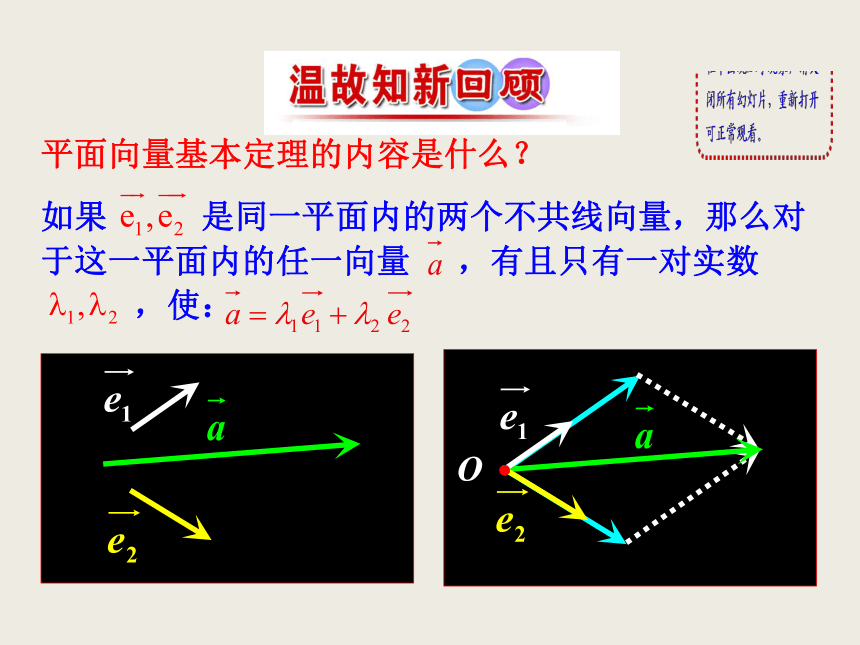
2.3.3 平面向量的坐标运算平面向量基本定理的内容是什么?如果 是同一平面内的两个不共线向量,那么对
于这一平面内的任一向量 ,有且只有一对实数
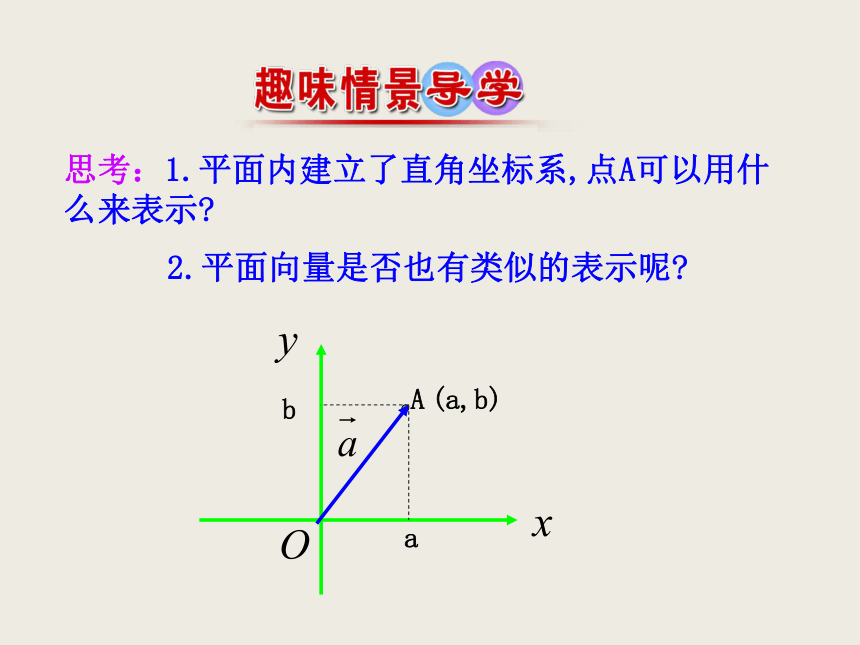
,使:画一画,算一算思考:从这个问题中,你认为选取哪组基底对向量 进行分解比较简单?思考:1.平面内建立了直角坐标系,点A可以用什么来表示?2.平面向量是否也有类似的表示呢?A(a,b)ab1.理解平面向量的坐标的概念;会进行平面向量的正交分解.
2.掌握平面向量的坐标运算.(重点) 把一个向量分解为两个互相垂直的向量,叫做把向量正交分解. 由平面向量的基本定理知,对平面上任意向量 ,
均可以分解为不共线的两个向量 和 ,
使 如图,在光滑斜面上一个木
块受到重力 的作用,产生两个
效果,一是木块受平行于斜面的
力 的作用,沿斜面下滑;一是
木块产生垂直于斜面的压力
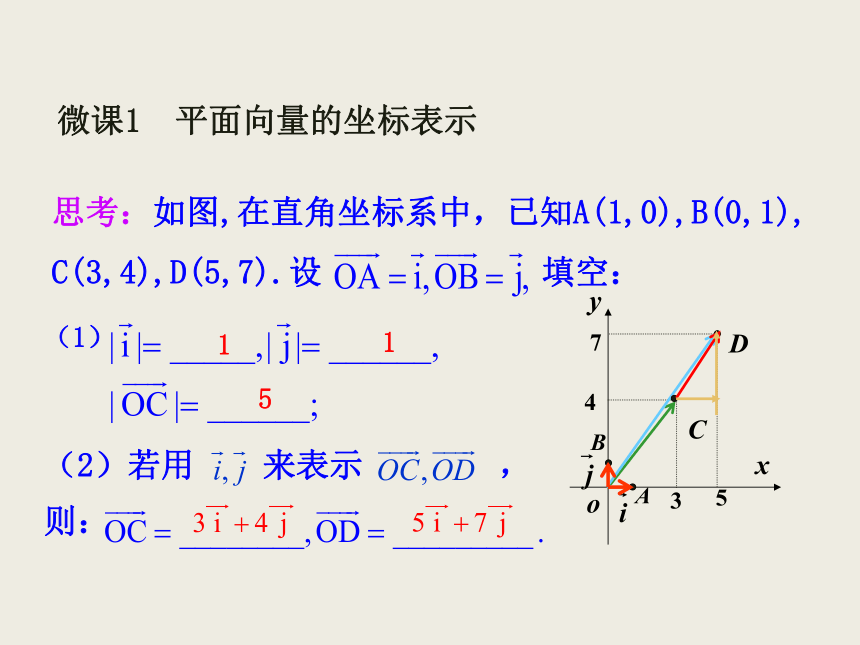
叫做把重力 分解.思考:如图,在直角坐标系中,已知A(1,0),B(0,1),
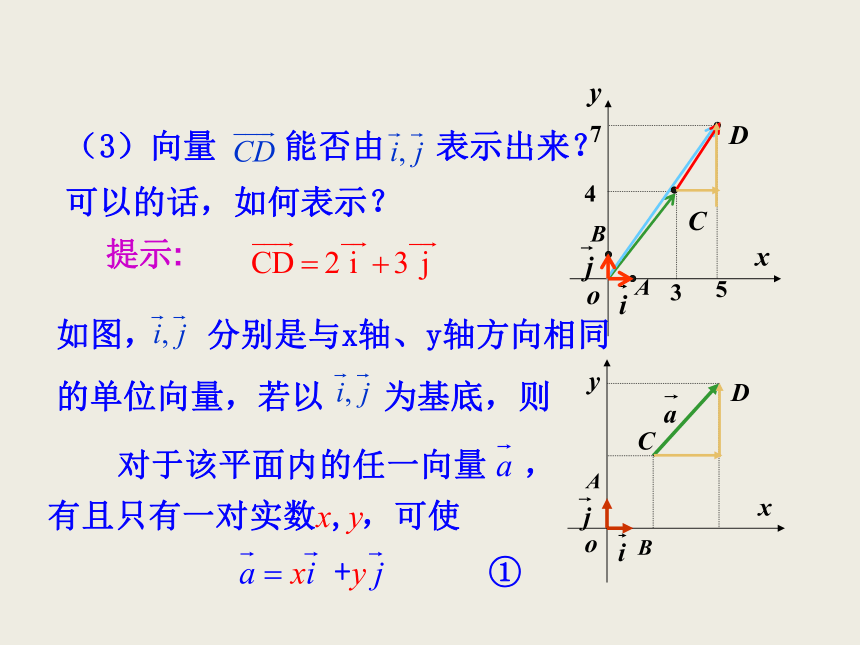
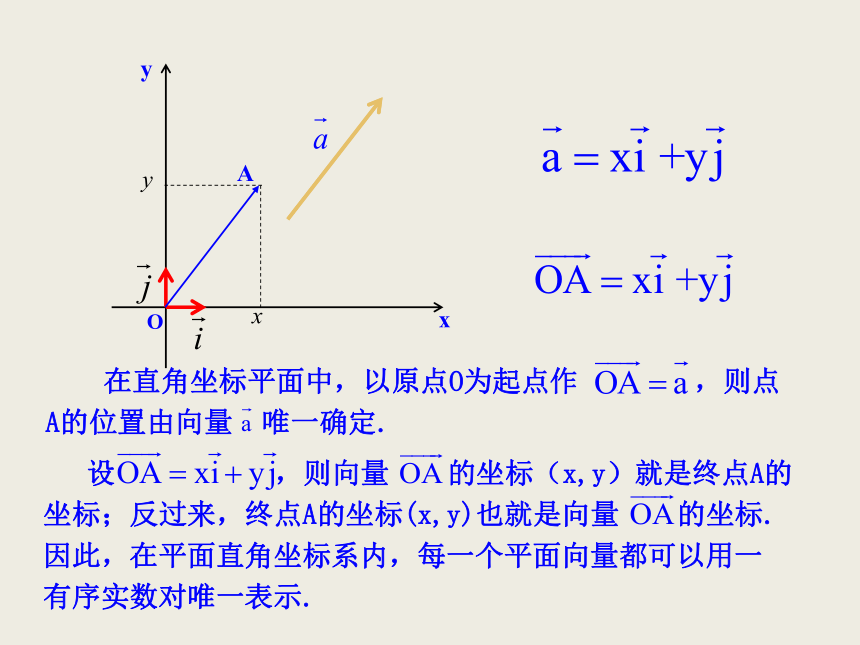
C(3,4),D(5,7).设 填空:(1)(2)若用 来表示 ,则:115微课1 平面向量的坐标表示(3)向量 能否由 表示出来?可以的话,如何表示?提示:② 这样,平面内的任一向量 都可由x,y唯一确定,我们把有序数对(x,y)叫做向量 的坐标,记作显然,OxyA 在直角坐标平面中,以原点O为起点作 ,则点
A的位置由向量 唯一确定. 设 ,则向量 的坐标(x,y)就是终点A的
坐标;反过来,终点A的坐标(x,y)也就是向量 的坐标.
因此,在平面直角坐标系内,每一个平面向量都可以用一
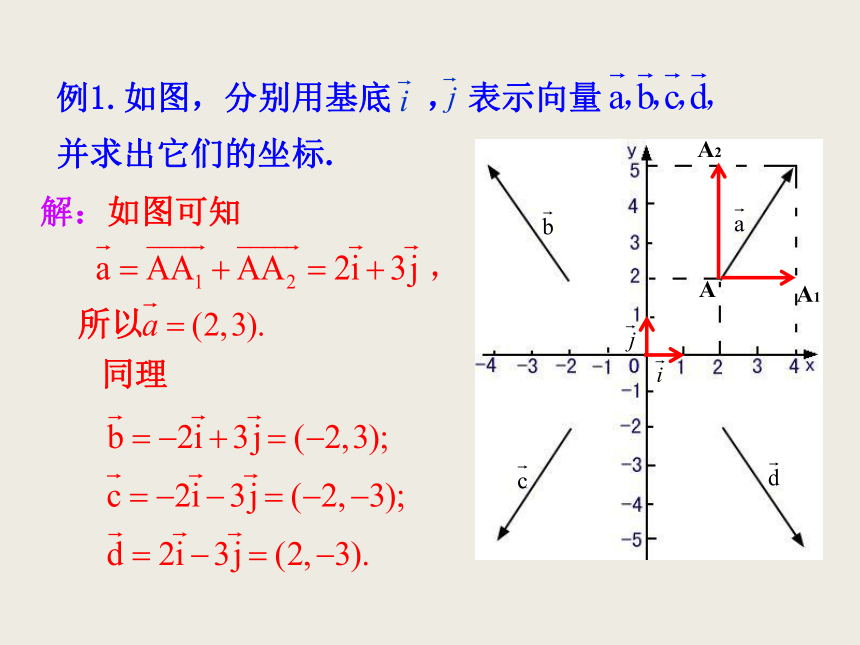
有序实数对唯一表示.答案:写出下列向量的坐标,其中 是与x轴,y轴方向相同的单位向量.【即时训练】例1.如图,分别用基底 , 表示向量
并求出它们的坐标.AA1A2解:如图可知同理 如图,用基底 分别表示向量 ,并求出它们的坐标.【变式练习】微课2 平面向量的坐标运算思考:已知 ,你能得出
的坐标吗?由向量线性运算的结合律和分配律可得提示: 两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差). 实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.即同理可得C【即时训练】例2.如图,已知 ,求 的坐标.xyOB(x2,y2)A(x1,y1)【解析】 一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标.【方法规律】小结:平面向量的坐标运算A【变式练习】例3.已知 ,求 的坐标. 设平面向量a=(3,5),b=(-2,1),则a-2b=( ) A.(6,3) B.(7,3)
C.(2,1) D.(7,2)B【变式练习】例4.如图,已知□ABCD的三个顶点A,B,C的坐标分别是
(-2,1),(-1,3),(3,4),试求顶点D的坐标.ABCDxyO解法1:如图,设顶点D的坐标为(x,y).解得所以顶点D的坐标为(2,2).-2 -11 2 34
3
2
1ABCDxyO解法2:如图,由平行四边形法则可得而所以顶点D的坐标为(2,2).-2 -11 2 34
3
2
1【解题关键】求向量起点坐标、终点坐标→用终点坐标减去起点坐标→向量的坐标.【变式练习】DDDC5.已知点A(3,1), ,若向量 ,
O为坐标原点,则x=________,y=_________.-45平面向量坐标表示结构图平面向量坐标表示定义向量运算的坐标表示向量平行的坐标表示加法减法实数与向量的积2.平面向量的坐标运算要及时把握梦想,因为梦想一死,生命就如一只羽翼受创的小鸟,无法飞翔.
——兰斯顿?休斯
2.3.3 平面向量的坐标运算平面向量基本定理的内容是什么?如果 是同一平面内的两个不共线向量,那么对
于这一平面内的任一向量 ,有且只有一对实数
,使:画一画,算一算思考:从这个问题中,你认为选取哪组基底对向量 进行分解比较简单?思考:1.平面内建立了直角坐标系,点A可以用什么来表示?2.平面向量是否也有类似的表示呢?A(a,b)ab1.理解平面向量的坐标的概念;会进行平面向量的正交分解.
2.掌握平面向量的坐标运算.(重点) 把一个向量分解为两个互相垂直的向量,叫做把向量正交分解. 由平面向量的基本定理知,对平面上任意向量 ,
均可以分解为不共线的两个向量 和 ,
使 如图,在光滑斜面上一个木
块受到重力 的作用,产生两个
效果,一是木块受平行于斜面的
力 的作用,沿斜面下滑;一是
木块产生垂直于斜面的压力
叫做把重力 分解.思考:如图,在直角坐标系中,已知A(1,0),B(0,1),
C(3,4),D(5,7).设 填空:(1)(2)若用 来表示 ,则:115微课1 平面向量的坐标表示(3)向量 能否由 表示出来?可以的话,如何表示?提示:② 这样,平面内的任一向量 都可由x,y唯一确定,我们把有序数对(x,y)叫做向量 的坐标,记作显然,OxyA 在直角坐标平面中,以原点O为起点作 ,则点
A的位置由向量 唯一确定. 设 ,则向量 的坐标(x,y)就是终点A的
坐标;反过来,终点A的坐标(x,y)也就是向量 的坐标.
因此,在平面直角坐标系内,每一个平面向量都可以用一
有序实数对唯一表示.答案:写出下列向量的坐标,其中 是与x轴,y轴方向相同的单位向量.【即时训练】例1.如图,分别用基底 , 表示向量
并求出它们的坐标.AA1A2解:如图可知同理 如图,用基底 分别表示向量 ,并求出它们的坐标.【变式练习】微课2 平面向量的坐标运算思考:已知 ,你能得出
的坐标吗?由向量线性运算的结合律和分配律可得提示: 两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差). 实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.即同理可得C【即时训练】例2.如图,已知 ,求 的坐标.xyOB(x2,y2)A(x1,y1)【解析】 一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标.【方法规律】小结:平面向量的坐标运算A【变式练习】例3.已知 ,求 的坐标. 设平面向量a=(3,5),b=(-2,1),则a-2b=( ) A.(6,3) B.(7,3)
C.(2,1) D.(7,2)B【变式练习】例4.如图,已知□ABCD的三个顶点A,B,C的坐标分别是
(-2,1),(-1,3),(3,4),试求顶点D的坐标.ABCDxyO解法1:如图,设顶点D的坐标为(x,y).解得所以顶点D的坐标为(2,2).-2 -11 2 34
3
2
1ABCDxyO解法2:如图,由平行四边形法则可得而所以顶点D的坐标为(2,2).-2 -11 2 34
3
2
1【解题关键】求向量起点坐标、终点坐标→用终点坐标减去起点坐标→向量的坐标.【变式练习】DDDC5.已知点A(3,1), ,若向量 ,
O为坐标原点,则x=________,y=_________.-45平面向量坐标表示结构图平面向量坐标表示定义向量运算的坐标表示向量平行的坐标表示加法减法实数与向量的积2.平面向量的坐标运算要及时把握梦想,因为梦想一死,生命就如一只羽翼受创的小鸟,无法飞翔.
——兰斯顿?休斯
