2019人教A版数学必修四课件:第二章 平面向量 2.3.1 平面向量基本定理(情境互动课型)(35张PPT)
文档属性
| 名称 | 2019人教A版数学必修四课件:第二章 平面向量 2.3.1 平面向量基本定理(情境互动课型)(35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-14 18:21:57 | ||
图片预览






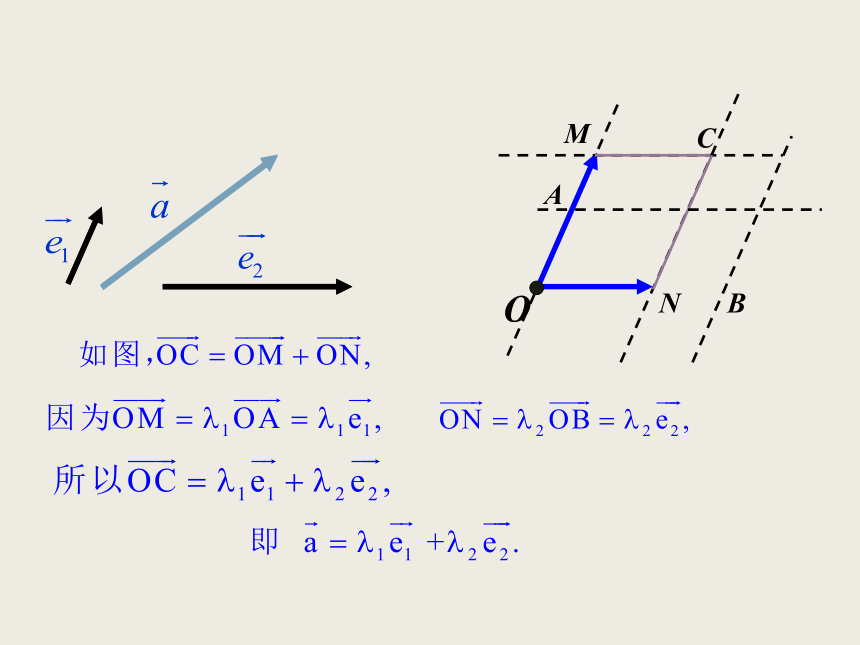
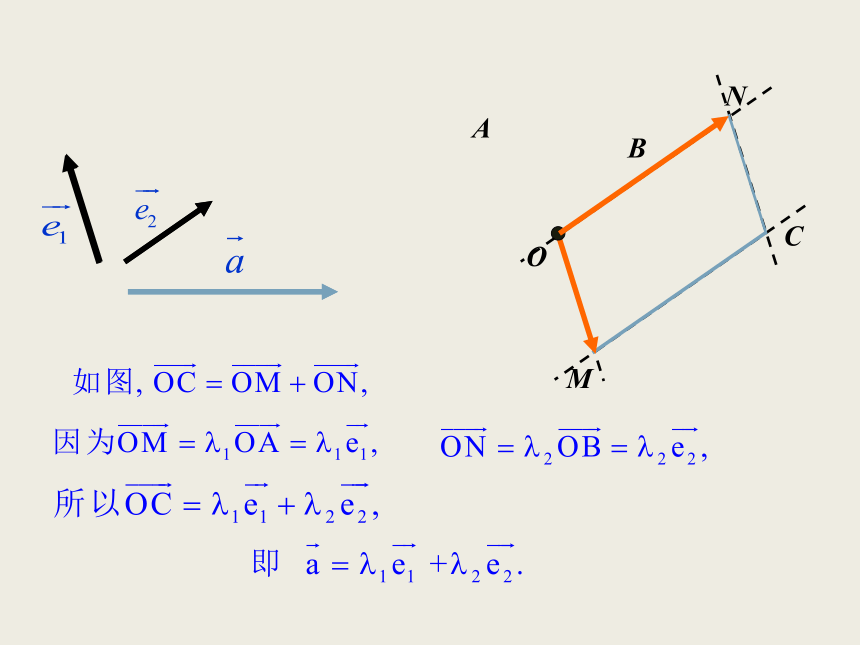



文档简介
课件35张PPT。2.3 平面向量的基本定理及坐标表示
2.3.1 平面向量基本定理当 时, 与 同向,且 是 的 倍;当 时, 与 反向,且 是 的 倍;当 时, ,且 .⑴向量共线定理当且仅当有唯一一个实数⑵向量的加法:OBCAOAB平行四边形法则三角形法则共起点首尾相接思考:(1)向量 是否可以用含有
的式子来表示呢?怎样表示?(2)若向量 能够用 表示,这种表示是否唯一?请说明理由.1.理解平面向量的基底的意义与作用. (重点)
2.能够在具体问题中适当地选取基底,使其他向量都能够用基底来表达. (难点)
3.初步利用定理解决问题(如相交线交成线段比的问题等). 一个平面内的两个不共线的向量 与该
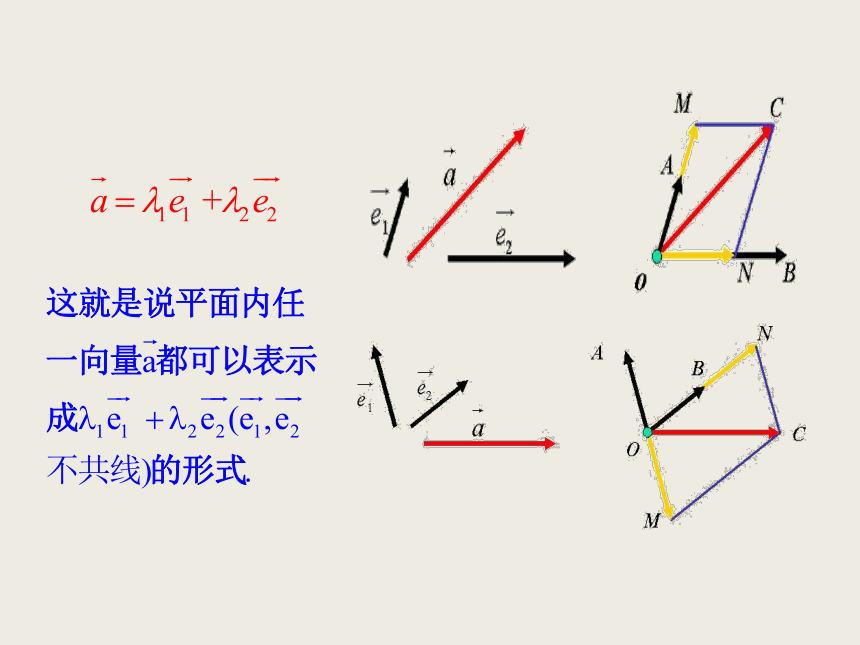
平面内的任一向量 之间的关系.微课1 平面向量基本定理NOCABMOCABMN 如果 , 是同一平面内的两个不共线向量,那
么对于这一平面内的任意向量 ,有且只有一对实
数λ1,λ2 ,使 说明:① , 是两个不共线的向量;
② 是平面内的任意向量;
③ λ1,λ2为实数,且唯一确定.平面向量基本定理 我们把不共线的向量 , 叫做这一平面内所有向量
的一组基底. 不共线向量有不同方向,它们的位置关系可用夹角来表示.关于向量的夹角,我们规定:AOB已知两个非零向量 .如图,叫做向量 与 的夹角.C【即时训练】OABCA【变式练习】利用加法法则或减法法则【变式练习】A【互动探究】例3.已知A, B是l上任意两点,O是l外一点,求证:
对直线l上任一点P,存在实数t,使 关于基底
{ }的分解式为l【解析】根据平面向量基本定理,同一平面内任意向量都可以用两个不共线的向量表示,再由已知可得 已知 不共线,且 ,
若 共线,则 = .0【变式练习】BCC135°平面向量基本定理平面向量基本定理定理基底如果 是同一平面内的两个不共线向量,
那么对于这一平面内的任意向量 有且只有
一对实数 使 .不共线的向量 叫做表示这一平面内
所有向量的一组基底.言论的花,开得愈大;行为的果子,结得愈小.
——冰心
2.3.1 平面向量基本定理当 时, 与 同向,且 是 的 倍;当 时, 与 反向,且 是 的 倍;当 时, ,且 .⑴向量共线定理当且仅当有唯一一个实数⑵向量的加法:OBCAOAB平行四边形法则三角形法则共起点首尾相接思考:(1)向量 是否可以用含有
的式子来表示呢?怎样表示?(2)若向量 能够用 表示,这种表示是否唯一?请说明理由.1.理解平面向量的基底的意义与作用. (重点)
2.能够在具体问题中适当地选取基底,使其他向量都能够用基底来表达. (难点)
3.初步利用定理解决问题(如相交线交成线段比的问题等). 一个平面内的两个不共线的向量 与该
平面内的任一向量 之间的关系.微课1 平面向量基本定理NOCABMOCABMN 如果 , 是同一平面内的两个不共线向量,那
么对于这一平面内的任意向量 ,有且只有一对实
数λ1,λ2 ,使 说明:① , 是两个不共线的向量;
② 是平面内的任意向量;
③ λ1,λ2为实数,且唯一确定.平面向量基本定理 我们把不共线的向量 , 叫做这一平面内所有向量
的一组基底. 不共线向量有不同方向,它们的位置关系可用夹角来表示.关于向量的夹角,我们规定:AOB已知两个非零向量 .如图,叫做向量 与 的夹角.C【即时训练】OABCA【变式练习】利用加法法则或减法法则【变式练习】A【互动探究】例3.已知A, B是l上任意两点,O是l外一点,求证:
对直线l上任一点P,存在实数t,使 关于基底
{ }的分解式为l【解析】根据平面向量基本定理,同一平面内任意向量都可以用两个不共线的向量表示,再由已知可得 已知 不共线,且 ,
若 共线,则 = .0【变式练习】BCC135°平面向量基本定理平面向量基本定理定理基底如果 是同一平面内的两个不共线向量,
那么对于这一平面内的任意向量 有且只有
一对实数 使 .不共线的向量 叫做表示这一平面内
所有向量的一组基底.言论的花,开得愈大;行为的果子,结得愈小.
——冰心
