2019人教A版数学必修四课件:第二章 平面向量 2.2.2 向量减法运算及其几何意义(情境互动课型)(34张PPT)
文档属性
| 名称 | 2019人教A版数学必修四课件:第二章 平面向量 2.2.2 向量减法运算及其几何意义(情境互动课型)(34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-14 18:20:37 | ||
图片预览









文档简介
(共34张PPT)
2.2.2 向量减法运算及其几何意义
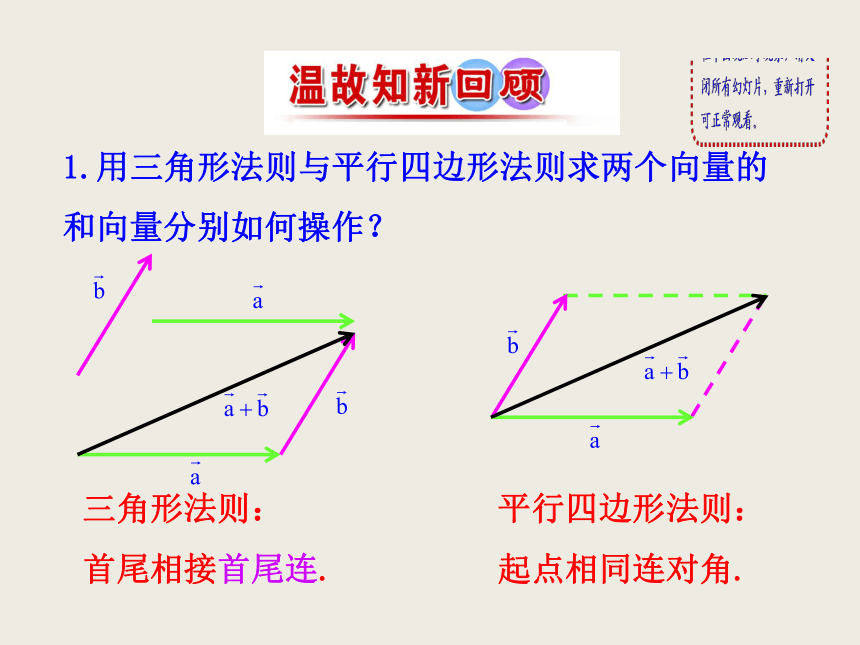
1.用三角形法则与平行四边形法则求两个向量的和向量分别如何操作?
三角形法则:
首尾相接首尾连.
平行四边形法则:
起点相同连对角.
2.向量的加法运算有哪些运算性质?
向量是否有减法?如何理解向量的减法?
我们知道,减去一个数等于加上这个数的相反数,向量的减法是否也有类似的法则?
1.了解相反向量的概念.
2.掌握向量的减法,会作两个向量的差向量,并理解其几何意义.(重、难点)
3.通过阐述向量的减法运算可以转化成向量的加法运算,使学生理解事物间可以相互转化的思想.
微课1 向量减法的含义
思考1:两个相反向量的和向量是什么?向量 的
相反向量可以怎样表示?
规定:零向量的相反向量仍是零向量.
思考2: 的相反向量是什么?零向量 的相反向量是什么?
提示:
思考3:在实数的运算中,减去一个数等于加上这个
数的相反数.据此原理,向量 可以怎样理解?
思考4:两个向量的差还是一个向量吗?
思考5:向量 加上向量 的相反向量,叫做 与
的差向量,求两个向量的差的运算叫做向量的减
法,对于向量
提示:是
提示:
C
【即时训练】
微课2 向量减法的几何意义
思考1:如果向量 与 同向,如何作出向量
提示:
思考2:如果向量 与 反向,如何作出向量
提示:
A
O
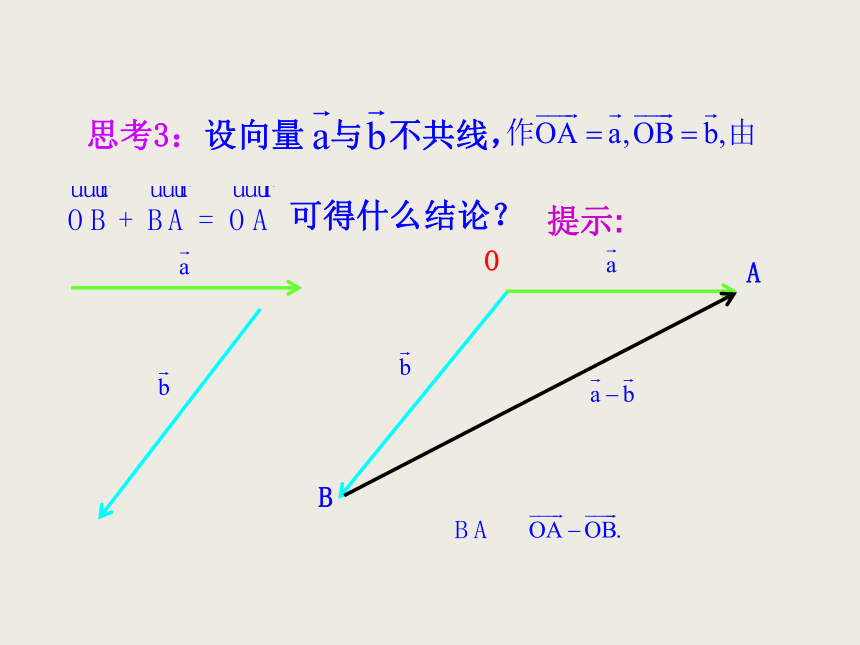
思考3:设向量 与 不共线,
可得什么结论?
B
提示:
C
D
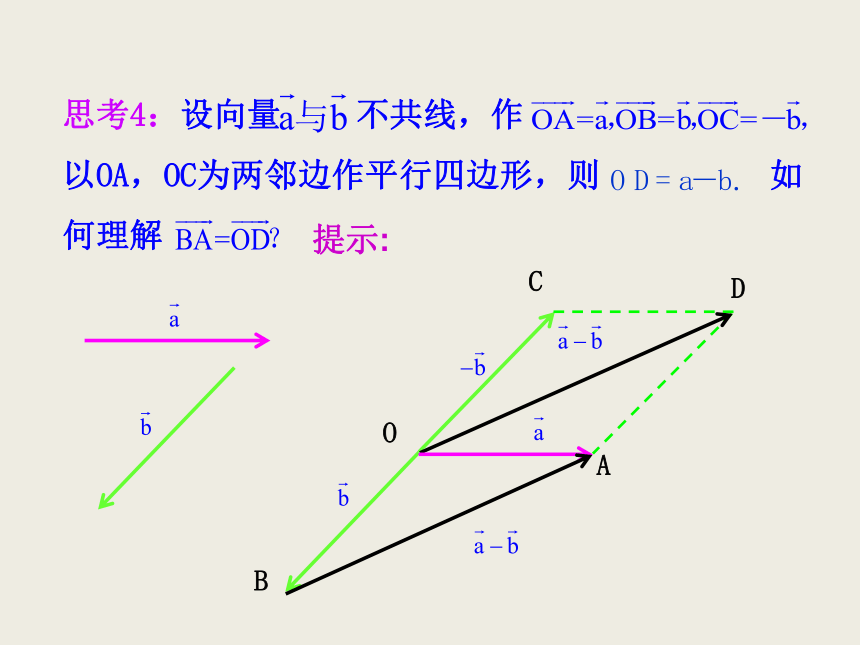
思考4:设向量 不共线,作
以OA,OC为两邻边作平行四边形,则 如
何理解
A
O
B
提示:
思考5:求作两个向量的差向量也有三角形法则和平行四边形法则,其中三角形法则的作图特点是什么?
首同尾连指被减
C
D
A
O
B
提示:
思考6:向量 是什么关系?
的大小关系如何?
当且仅当 反向时取等号;
当且仅当 同向时取等号.
是相反向量.
提示:
思考7: 有什么大小关系吗?为什么?
思考8:对于非零向量 可能相等吗?
A
B
C
O
提示:
提示:
如图,已知向量 ,求作向量
【即时训练】
O
A
B
C
D
【解析】在平面上任取一点O,作
再作 并以BA,BC为邻边作□ BADC,则
(如图所示)
则
a
b
c
d
O
A
B
C
D
作法:如图,在平面内任取一点O,作
例1.如图,已知向量 求作向量
(1)
(2)
(4)
,
,
b
a
.
b
a
-
求作
如图,已知
(3)
【变式练习】
例2.对下列各式进行化简
C
【变式练习】
例3.如图,□ABCD中, 表示
向量
A
D
B
C
解:由向量加法的平行四边形法则,
得
由向量的减法可得,
注意向量的方向
B
【变式练习】
A
C
A
C
0
东北方向
概念
三角形法则
向量减法
应用
1.知识结构
2.向量的减法
定义
几何
意义
向量 加上向量 的相反向量,叫做 的差,即
求两个向量差的运算,叫做向量的减法
如图,设 可以表示为从向量
的终点指向向量 的终点的向量
少而好学,如日出之阳;壮而好学,如日中之光;老而好学,如炳烛之明。
——刘向
2.2.2 向量减法运算及其几何意义
1.用三角形法则与平行四边形法则求两个向量的和向量分别如何操作?
三角形法则:
首尾相接首尾连.
平行四边形法则:
起点相同连对角.
2.向量的加法运算有哪些运算性质?
向量是否有减法?如何理解向量的减法?
我们知道,减去一个数等于加上这个数的相反数,向量的减法是否也有类似的法则?
1.了解相反向量的概念.
2.掌握向量的减法,会作两个向量的差向量,并理解其几何意义.(重、难点)
3.通过阐述向量的减法运算可以转化成向量的加法运算,使学生理解事物间可以相互转化的思想.
微课1 向量减法的含义
思考1:两个相反向量的和向量是什么?向量 的
相反向量可以怎样表示?
规定:零向量的相反向量仍是零向量.
思考2: 的相反向量是什么?零向量 的相反向量是什么?
提示:
思考3:在实数的运算中,减去一个数等于加上这个
数的相反数.据此原理,向量 可以怎样理解?
思考4:两个向量的差还是一个向量吗?
思考5:向量 加上向量 的相反向量,叫做 与
的差向量,求两个向量的差的运算叫做向量的减
法,对于向量
提示:是
提示:
C
【即时训练】
微课2 向量减法的几何意义
思考1:如果向量 与 同向,如何作出向量
提示:
思考2:如果向量 与 反向,如何作出向量
提示:
A
O
思考3:设向量 与 不共线,
可得什么结论?
B
提示:
C
D
思考4:设向量 不共线,作
以OA,OC为两邻边作平行四边形,则 如
何理解
A
O
B
提示:
思考5:求作两个向量的差向量也有三角形法则和平行四边形法则,其中三角形法则的作图特点是什么?
首同尾连指被减
C
D
A
O
B
提示:
思考6:向量 是什么关系?
的大小关系如何?
当且仅当 反向时取等号;
当且仅当 同向时取等号.
是相反向量.
提示:
思考7: 有什么大小关系吗?为什么?
思考8:对于非零向量 可能相等吗?
A
B
C
O
提示:
提示:
如图,已知向量 ,求作向量
【即时训练】
O
A
B
C
D
【解析】在平面上任取一点O,作
再作 并以BA,BC为邻边作□ BADC,则
(如图所示)
则
a
b
c
d
O
A
B
C
D
作法:如图,在平面内任取一点O,作
例1.如图,已知向量 求作向量
(1)
(2)
(4)
,
,
b
a
.
b
a
-
求作
如图,已知
(3)
【变式练习】
例2.对下列各式进行化简
C
【变式练习】
例3.如图,□ABCD中, 表示
向量
A
D
B
C
解:由向量加法的平行四边形法则,
得
由向量的减法可得,
注意向量的方向
B
【变式练习】
A
C
A
C
0
东北方向
概念
三角形法则
向量减法
应用
1.知识结构
2.向量的减法
定义
几何
意义
向量 加上向量 的相反向量,叫做 的差,即
求两个向量差的运算,叫做向量的减法
如图,设 可以表示为从向量
的终点指向向量 的终点的向量
少而好学,如日出之阳;壮而好学,如日中之光;老而好学,如炳烛之明。
——刘向
