沪科版数学七年级下册8.3.1完全平方公式 课件 (29张PPT)
文档属性
| 名称 | 沪科版数学七年级下册8.3.1完全平方公式 课件 (29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-15 00:00:00 | ||
图片预览







文档简介
课件29张PPT。8.3完全平方公式
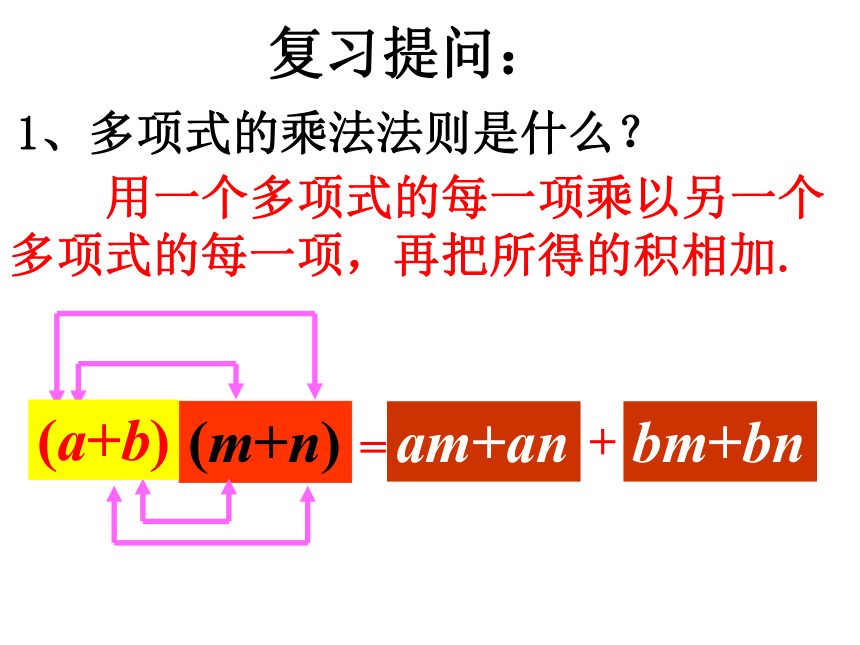
复习提问: 用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.1、多项式的乘法法则是什么? am+anbm+bn+=(m+n)(a+b)情境导入一位老人非常喜欢孩子,每当有孩子到他家做客时,他都要拿出糖果招待他们,来1个孩子就给这个孩子1块糖;来2个孩子就给每人2块糖;来了3个孩子就给每人3块糖……
(1)第一天有a个孩子去他家,老人一共给这些孩子多少块糖?
(2)第二天有b个孩子去他家,老人一共给这些孩子多少块糖?情景导入(3)第三天有(a+b)个孩子去他家,老人一共要给这些孩子多少块糖果?
解答(1)第一天供给孩子a2块糖果;
(2)第二天共给孩子们b2块糖果;
(3)第三天供给孩子们(a+b)2块糖果。
(a+b)2等于什么?这就是我们这节课要研究的内容……(4)(m-2) 2_=__________(3)(p-1)2=(p-1)(p-1)=_________(2)(m+2)2=__________计算下列各式,你能发现什么规律?
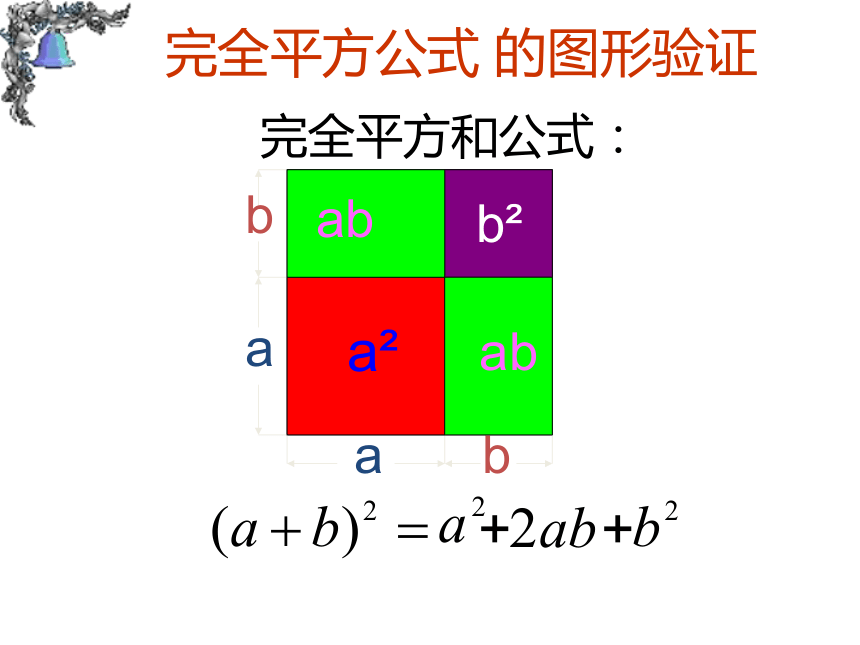
(1)( p+1)2=(p+1)(p+1)=_________p2+2p+1m2+4m+4p2-2p+1m2-4m+4实践探究交流新知一、二、猜想结论:(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2三、验证结论(a+b)2(a-b)2= a2 +2ab+b2= a2 - 2ab+b2= a2 +ab +ab +b2= a2 - ab - ab +b2=(a+b) (a+b)=(a-b) (a-b)完全平方公式的数学表达式:完全平方公式的文字叙述: 两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。 归纳总结(a+b)2a2b2完全平方和公式:完全平方公式 的图形验证(a-b)2b2完全平方差公式:完全平方公式 的图形验证公式特点:4、公式中的字母a,b可以表示数,单项式和
多项式。(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、积为二次三项式;2、积中两项为两数的平方和;3、另一项是两数积的2倍,且与乘式中
间的符号相同。首平方,末平方,首末两倍放 中央 1、 判断下面各式是否正确?如果不正确,应当怎样改正? (x+y)2=x2 +y2(2) (x-y)2 =x2 -y2(3) (x-y)2 =x2+2xy +y2(4) (x+y)2 =x2 +xy +y2错错错错(x+y)2 =x2+2xy +y2(x-y)2 =x2 -2xy+y2(x -y)2 =x2 -2xy +y2(x +y)2 =x2+2xy +y2感受新知(2) (a - b)2 与 (b - a)2
(3) (-b +a)2 与(-a +b)2(1) (-a -b)2 与(a+b)22、比较下列各式之间的关系:相等相等相等例1 运用完全平方公式计算:解: (x+2y)2==x2(x+2y)2(a +b)2= a2 + 2 ab + b2x2+2 · x · 2y+(2y)2+4xy+4y2应用举例(1)解: (x-2y)2==x2(x-2y)2(a - b)2= a2 - 2 ab + b2x2-2 · x · 2y+(2y)2-4xy+4y2(2)例2 计算:(-a+b)2 =(b-a)2解:原式=(-a-b)2 =(a+b)2解:原式=练习1:运用完全平方公式计算:(1)(x+6)2(2)( y-5)2(3)(-2x+5)2课堂练习巩固新知解: (x+6)2==x2(1)(x+6)2(a +b)2= a2 + 2 ab + b2x2+2 · x · 6+ 62+12x+36解: (y - 5)2==y2(2)(y - 5)2(a - b)2= a2 - 2 ab + b2y2+2 · y · 5+ 52- 10y+25解:(-2x+5)2== -4x2(3)( -2x+5)2(a +b)2 = a2 + 2 ab + b2(-2x)2+2·(-2x)·5+ 52-20x+251992= 8.92=练习2、利用完全平方公式计算:(1)(2)利用完全平方公式计算:解: (1)8.92= (8+0.9)2=64+1.44+0.81=66.25 (2)1992= (200 - 1)2=40000 - 200+1=39799如何计算 (a+b+c)2解: (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2·(a+b)·c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc1、2、思考(1)(a+b)2与(a-b)2有什么关系?
(2)a2+b2与(a+b)2与(a-b)2有什么关系?
(3)2ab与(a+b)2与(a-b)2有什么关系?
解答:(1) (a+b)2=(a-b)2+4ab
(2) a2+b2=(a+b)2-2ab
a2+b2=(a-b)2+2ab
(3) 4ab=(a+b)2-(a-b)2通过这节课的学习你学到了什么课堂小结(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、完全平方公式:2、注意:项数、符号、字母及
其指数;3、完全平方公式的变形(a+b)2=(a-b)2+4ab
a2+b2=(a+b)2-2ab
a2+b2=(a-b)2+2ab作业布置:P69练习第1题和第2题P71-p73习题8.3第1题和第8题谢谢各位同学
再见!
复习提问: 用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.1、多项式的乘法法则是什么? am+anbm+bn+=(m+n)(a+b)情境导入一位老人非常喜欢孩子,每当有孩子到他家做客时,他都要拿出糖果招待他们,来1个孩子就给这个孩子1块糖;来2个孩子就给每人2块糖;来了3个孩子就给每人3块糖……
(1)第一天有a个孩子去他家,老人一共给这些孩子多少块糖?
(2)第二天有b个孩子去他家,老人一共给这些孩子多少块糖?情景导入(3)第三天有(a+b)个孩子去他家,老人一共要给这些孩子多少块糖果?
解答(1)第一天供给孩子a2块糖果;
(2)第二天共给孩子们b2块糖果;
(3)第三天供给孩子们(a+b)2块糖果。
(a+b)2等于什么?这就是我们这节课要研究的内容……(4)(m-2) 2_=__________(3)(p-1)2=(p-1)(p-1)=_________(2)(m+2)2=__________计算下列各式,你能发现什么规律?
(1)( p+1)2=(p+1)(p+1)=_________p2+2p+1m2+4m+4p2-2p+1m2-4m+4实践探究交流新知一、二、猜想结论:(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2三、验证结论(a+b)2(a-b)2= a2 +2ab+b2= a2 - 2ab+b2= a2 +ab +ab +b2= a2 - ab - ab +b2=(a+b) (a+b)=(a-b) (a-b)完全平方公式的数学表达式:完全平方公式的文字叙述: 两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。 归纳总结(a+b)2a2b2完全平方和公式:完全平方公式 的图形验证(a-b)2b2完全平方差公式:完全平方公式 的图形验证公式特点:4、公式中的字母a,b可以表示数,单项式和
多项式。(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、积为二次三项式;2、积中两项为两数的平方和;3、另一项是两数积的2倍,且与乘式中
间的符号相同。首平方,末平方,首末两倍放 中央 1、 判断下面各式是否正确?如果不正确,应当怎样改正? (x+y)2=x2 +y2(2) (x-y)2 =x2 -y2(3) (x-y)2 =x2+2xy +y2(4) (x+y)2 =x2 +xy +y2错错错错(x+y)2 =x2+2xy +y2(x-y)2 =x2 -2xy+y2(x -y)2 =x2 -2xy +y2(x +y)2 =x2+2xy +y2感受新知(2) (a - b)2 与 (b - a)2
(3) (-b +a)2 与(-a +b)2(1) (-a -b)2 与(a+b)22、比较下列各式之间的关系:相等相等相等例1 运用完全平方公式计算:解: (x+2y)2==x2(x+2y)2(a +b)2= a2 + 2 ab + b2x2+2 · x · 2y+(2y)2+4xy+4y2应用举例(1)解: (x-2y)2==x2(x-2y)2(a - b)2= a2 - 2 ab + b2x2-2 · x · 2y+(2y)2-4xy+4y2(2)例2 计算:(-a+b)2 =(b-a)2解:原式=(-a-b)2 =(a+b)2解:原式=练习1:运用完全平方公式计算:(1)(x+6)2(2)( y-5)2(3)(-2x+5)2课堂练习巩固新知解: (x+6)2==x2(1)(x+6)2(a +b)2= a2 + 2 ab + b2x2+2 · x · 6+ 62+12x+36解: (y - 5)2==y2(2)(y - 5)2(a - b)2= a2 - 2 ab + b2y2+2 · y · 5+ 52- 10y+25解:(-2x+5)2== -4x2(3)( -2x+5)2(a +b)2 = a2 + 2 ab + b2(-2x)2+2·(-2x)·5+ 52-20x+251992= 8.92=练习2、利用完全平方公式计算:(1)(2)利用完全平方公式计算:解: (1)8.92= (8+0.9)2=64+1.44+0.81=66.25 (2)1992= (200 - 1)2=40000 - 200+1=39799如何计算 (a+b+c)2解: (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2·(a+b)·c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc1、2、思考(1)(a+b)2与(a-b)2有什么关系?
(2)a2+b2与(a+b)2与(a-b)2有什么关系?
(3)2ab与(a+b)2与(a-b)2有什么关系?
解答:(1) (a+b)2=(a-b)2+4ab
(2) a2+b2=(a+b)2-2ab
a2+b2=(a-b)2+2ab
(3) 4ab=(a+b)2-(a-b)2通过这节课的学习你学到了什么课堂小结(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、完全平方公式:2、注意:项数、符号、字母及
其指数;3、完全平方公式的变形(a+b)2=(a-b)2+4ab
a2+b2=(a+b)2-2ab
a2+b2=(a-b)2+2ab作业布置:P69练习第1题和第2题P71-p73习题8.3第1题和第8题谢谢各位同学
再见!
