沪科版数学八年级 19.2 平行四边形的判定课(24张PPT)
文档属性
| 名称 | 沪科版数学八年级 19.2 平行四边形的判定课(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-21 19:44:48 | ||
图片预览




文档简介
课件24张PPT。19.1.2平行四边形的判定濉溪县五沟中心学校 邵士彬19.1.2平行四边形的判定濉溪县五沟中心学校 邵士彬平行四边形的判定1、经历并了解平行四边形的判别方法探索过程,我们可以逐步掌握说理的基本方法。
2、探索并了解平行四边形的判别方法:能根据判别方法进行有关的应用。
3、在探索过程中发展我们的合理推理意识、主动探究的习惯。 4、体验数学活动来源于生活又服务于生活,提高我们的学习兴趣。 教学目标2.平行四边形具有哪些性质?知识回顾1.平行四边形的定义:两组对边分别平行的四边形是平行四边形思考:通过前面的学习,我们知道平行四边形对边相等、对角相等、对角线互相平分。
这些逆命题是不是真命题呢?
两组对边相等的四边形是平行四边形(?)
对角线互相平分的四边形平行四边形(?)
两组对角相等的四边形是平行四边形(?) 逆命题探究1:将两长两短的四根细木条用小钉顺次钉在一起,做成一个四边形,使等长的木条成为对边。它是平行四边形吗?
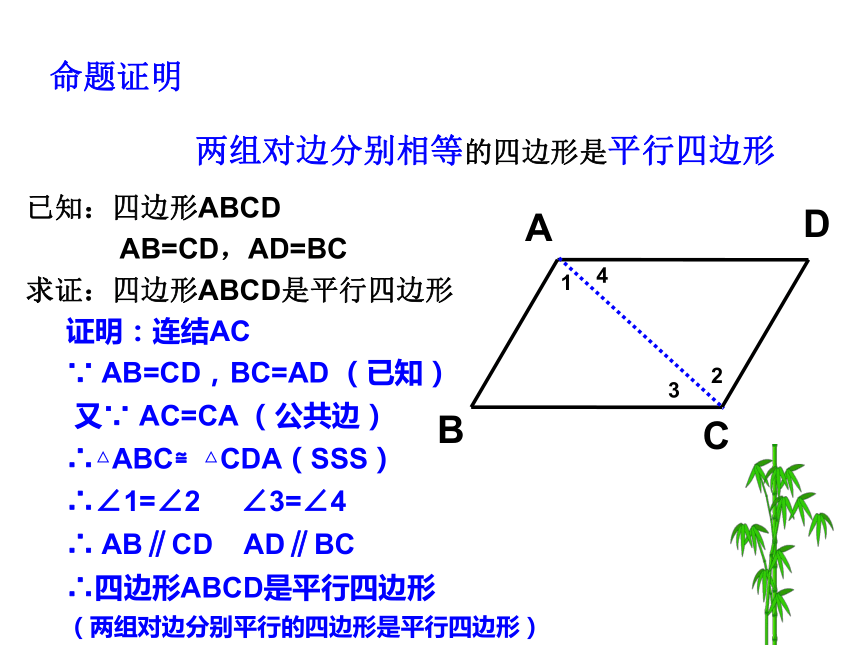
ABCD两组对边分别相等的四边形是平行四边形已知:四边形ABCD
AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:连结AC
∵ AB=CD,BC=AD (已知)
又∵ AC=CA (公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2 ∠3=∠4
∴ AB∥CD AD∥BC
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)命题证明判定定理1
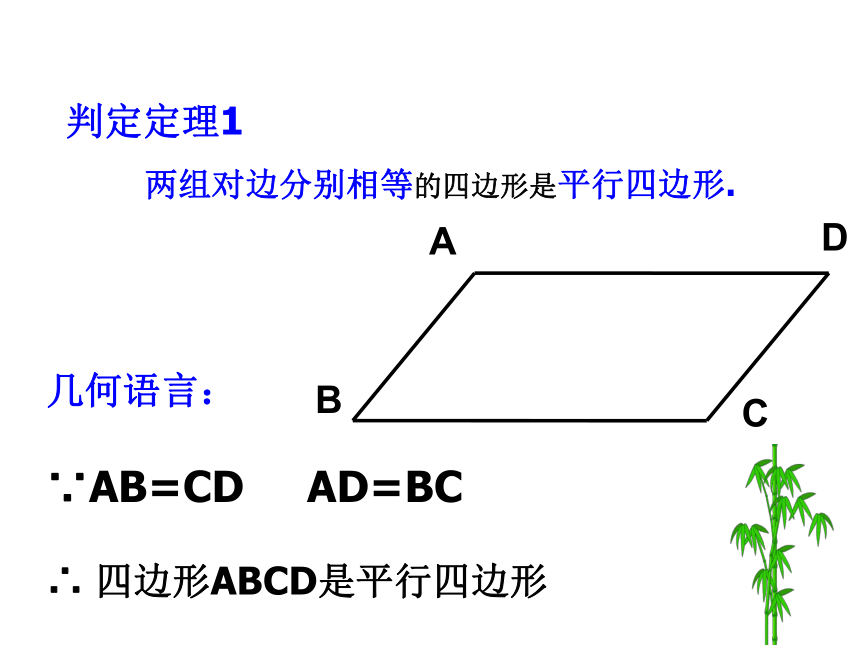
两组对边分别相等的四边形是平行四边形.
几何语言:
∵AB=CD AD=BC
∴ 四边形ABCD是平行四边形
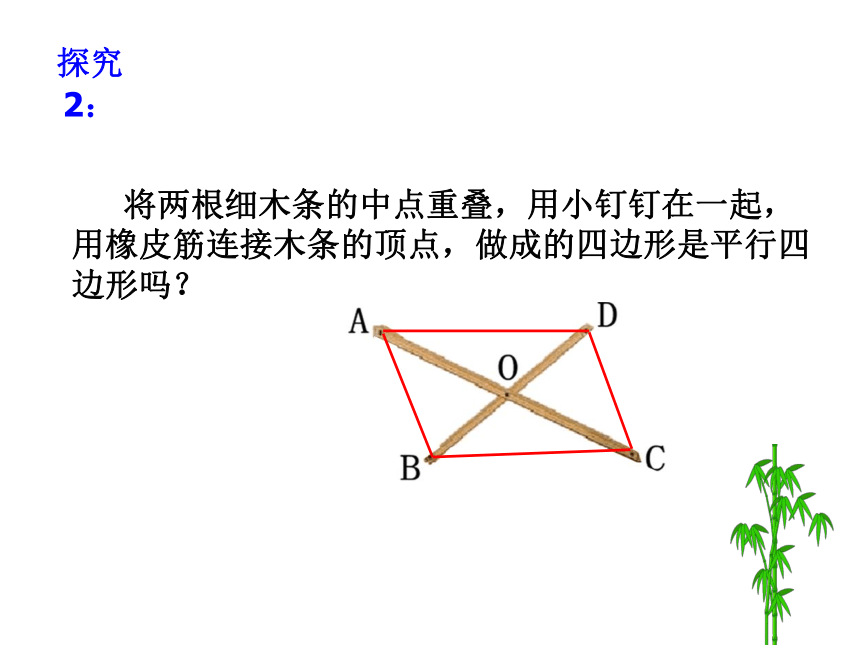
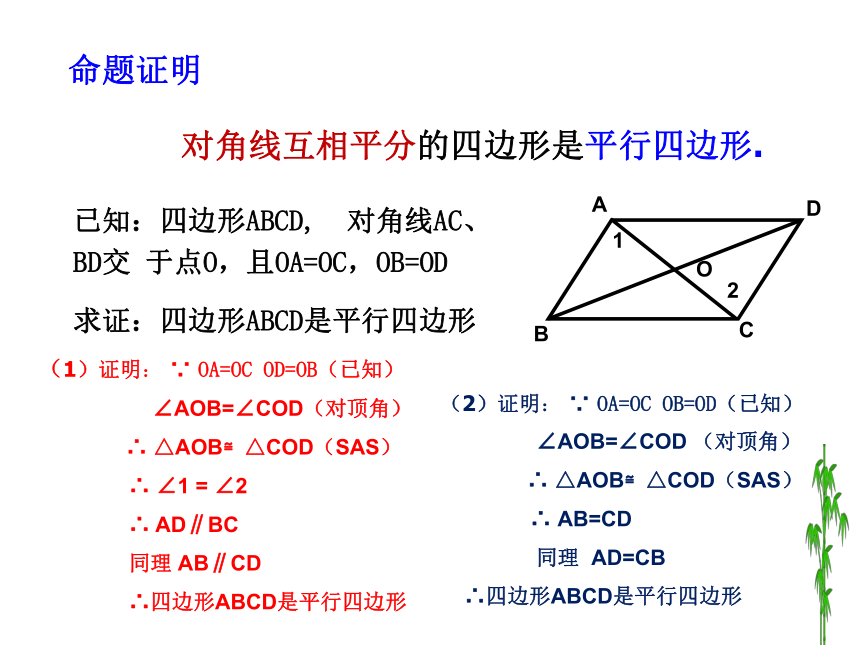
将两根细木条的中点重叠,用小钉钉在一起,用橡皮筋连接木条的顶点,做成的四边形是平行四边形吗?探究2:对角线互相平分的四边形是平行四边形.已知:四边形ABCD, 对角线AC、BD交 于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形命题证明判定定理2
对角线互相平分的四边形是平行四边形.
符号语言:
∵ OA=OC OB=OD
∴四边形ABCD是平行四边形 将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?四边形ABCD是什么样的图形? 将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?四边形ABCD是什么样的图形?探究3:已知:四边形ABCD中 AB∥CD, AB=CD求证:四边形ABCD是平行 四边形证明:连接BD一组对边平行且相等的四边形是平行四边形.命题证明判定定理3
一组对边平行且相等的四边形是平行四边形.
符号语言:
∵AD=BC AD ∥ BC
∴ 四边形ABCD是平行四边形
从边来判定1、两组对边分别平行的四边形是平行四边形 2、两组对边分别相等的四边形是平行四边形从对角线来判定4.两条对角线互相平分的四边形是平行四边形理一理平行四边形的判定方法 3、一组对边平行且相等的四边形是平 行四边形.
试一试判断下列四边形是否是平行四边形?并说明理由.⑴⑶4.8㎝BADC4.8㎝7.6㎝7.6㎝⑵7.6㎝7.6㎝AD∥BC 大显身手已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
1.在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= ___ cm, CD= ____cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO=__ cm, DO= ____cm时,四边形ABCD为平行四边形.
(3)若AD=BC时, AD BC 时,四边形ABCD为平行四边形.
2、在下列条件中,不能判定四边形是平行四边形的是( )
(两组对边分别平行)(两组对边分别相等)D8445(一组对边平行且相等)(A) AB∥CD,AD∥BC
(B) AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BCO∥____练习通过本节课的学习你收获了什么?
体会.分享BDAC已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)
3 如图,AB=DC=EF,AD=BC,DE=CF,图中有哪 些互相平行的线段?解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF AD∥BC AB=DC AD=BC四边形ABCD是平行四边形AB∥DCDC∥EF DC=EF DE=CF四边形CDEF是平行四边形DE∥CFAB∥ DC∥EF理由如下:3拓展题 已知:平行四边形ABCD中,E.F分别是边AD BC的中点,求证:EB=DF 已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形DABCEF改一改,证一证BE∥DF谢谢再见
2、探索并了解平行四边形的判别方法:能根据判别方法进行有关的应用。
3、在探索过程中发展我们的合理推理意识、主动探究的习惯。 4、体验数学活动来源于生活又服务于生活,提高我们的学习兴趣。 教学目标2.平行四边形具有哪些性质?知识回顾1.平行四边形的定义:两组对边分别平行的四边形是平行四边形思考:通过前面的学习,我们知道平行四边形对边相等、对角相等、对角线互相平分。
这些逆命题是不是真命题呢?
两组对边相等的四边形是平行四边形(?)
对角线互相平分的四边形平行四边形(?)
两组对角相等的四边形是平行四边形(?) 逆命题探究1:将两长两短的四根细木条用小钉顺次钉在一起,做成一个四边形,使等长的木条成为对边。它是平行四边形吗?
ABCD两组对边分别相等的四边形是平行四边形已知:四边形ABCD
AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:连结AC
∵ AB=CD,BC=AD (已知)
又∵ AC=CA (公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2 ∠3=∠4
∴ AB∥CD AD∥BC
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)命题证明判定定理1
两组对边分别相等的四边形是平行四边形.
几何语言:
∵AB=CD AD=BC
∴ 四边形ABCD是平行四边形
将两根细木条的中点重叠,用小钉钉在一起,用橡皮筋连接木条的顶点,做成的四边形是平行四边形吗?探究2:对角线互相平分的四边形是平行四边形.已知:四边形ABCD, 对角线AC、BD交 于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形命题证明判定定理2
对角线互相平分的四边形是平行四边形.
符号语言:
∵ OA=OC OB=OD
∴四边形ABCD是平行四边形 将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?四边形ABCD是什么样的图形? 将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?四边形ABCD是什么样的图形?探究3:已知:四边形ABCD中 AB∥CD, AB=CD求证:四边形ABCD是平行 四边形证明:连接BD一组对边平行且相等的四边形是平行四边形.命题证明判定定理3
一组对边平行且相等的四边形是平行四边形.
符号语言:
∵AD=BC AD ∥ BC
∴ 四边形ABCD是平行四边形
从边来判定1、两组对边分别平行的四边形是平行四边形 2、两组对边分别相等的四边形是平行四边形从对角线来判定4.两条对角线互相平分的四边形是平行四边形理一理平行四边形的判定方法 3、一组对边平行且相等的四边形是平 行四边形.
试一试判断下列四边形是否是平行四边形?并说明理由.⑴⑶4.8㎝BADC4.8㎝7.6㎝7.6㎝⑵7.6㎝7.6㎝AD∥BC 大显身手已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
1.在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= ___ cm, CD= ____cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO=__ cm, DO= ____cm时,四边形ABCD为平行四边形.
(3)若AD=BC时, AD BC 时,四边形ABCD为平行四边形.
2、在下列条件中,不能判定四边形是平行四边形的是( )
(两组对边分别平行)(两组对边分别相等)D8445(一组对边平行且相等)(A) AB∥CD,AD∥BC
(B) AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BCO∥____练习通过本节课的学习你收获了什么?
体会.分享BDAC已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)
3 如图,AB=DC=EF,AD=BC,DE=CF,图中有哪 些互相平行的线段?解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF AD∥BC AB=DC AD=BC四边形ABCD是平行四边形AB∥DCDC∥EF DC=EF DE=CF四边形CDEF是平行四边形DE∥CFAB∥ DC∥EF理由如下:3拓展题 已知:平行四边形ABCD中,E.F分别是边AD BC的中点,求证:EB=DF 已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形DABCEF改一改,证一证BE∥DF谢谢再见
