【华师大版八年级下册进阶培优训练】第九讲 一次函数与反比例函数的综合应用培优辅导(含答案)
文档属性
| 名称 | 【华师大版八年级下册进阶培优训练】第九讲 一次函数与反比例函数的综合应用培优辅导(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-15 10:28:26 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第九讲
一次函数与反比例函数之专题突破培优辅导
在历年中考试题中一次函数和反比例函数常以综合题形式出现,这类试题不仅能考查两个函数的基本性质,而且能考查同学们综合分析问题的能力。现以以下典型例题为例,浅谈这类问题的解法,供参考。
典型例题
题型一:求同一坐标系下的图象
【例1】
已知函数与在同一直角坐标系中的图象大致如图1,则下列结论正确的是(
)
A.
B.
C.
D.
【变式题组】
1、在同一直角坐标系中,函数与的图象大致是(
)
A.
B.
C.
D.
2、当k>0时,反比例函数和一次函数的图象大致是(
)
题型二:一次函数与反比例函数结合求解析式,自变量的取值范围,面积等
【例2】如图,已知,是一次函数的图象和反比例函数的图象的两个交点.www-2-1-cnjy-com
(1)求一次函数、反比例函数的关系式;
(2)求△AOB的面积.
(3)当自变量x满足什么条件时,y1>y2
.(直接写出答案)
(4)将反比例函数的图象向右平移n(n>0)个单位,得到的新图象经过点(3,-4),求对应的函数关系式y3.(直接写出答案)2-1-c-n-j-y
【变式题组】
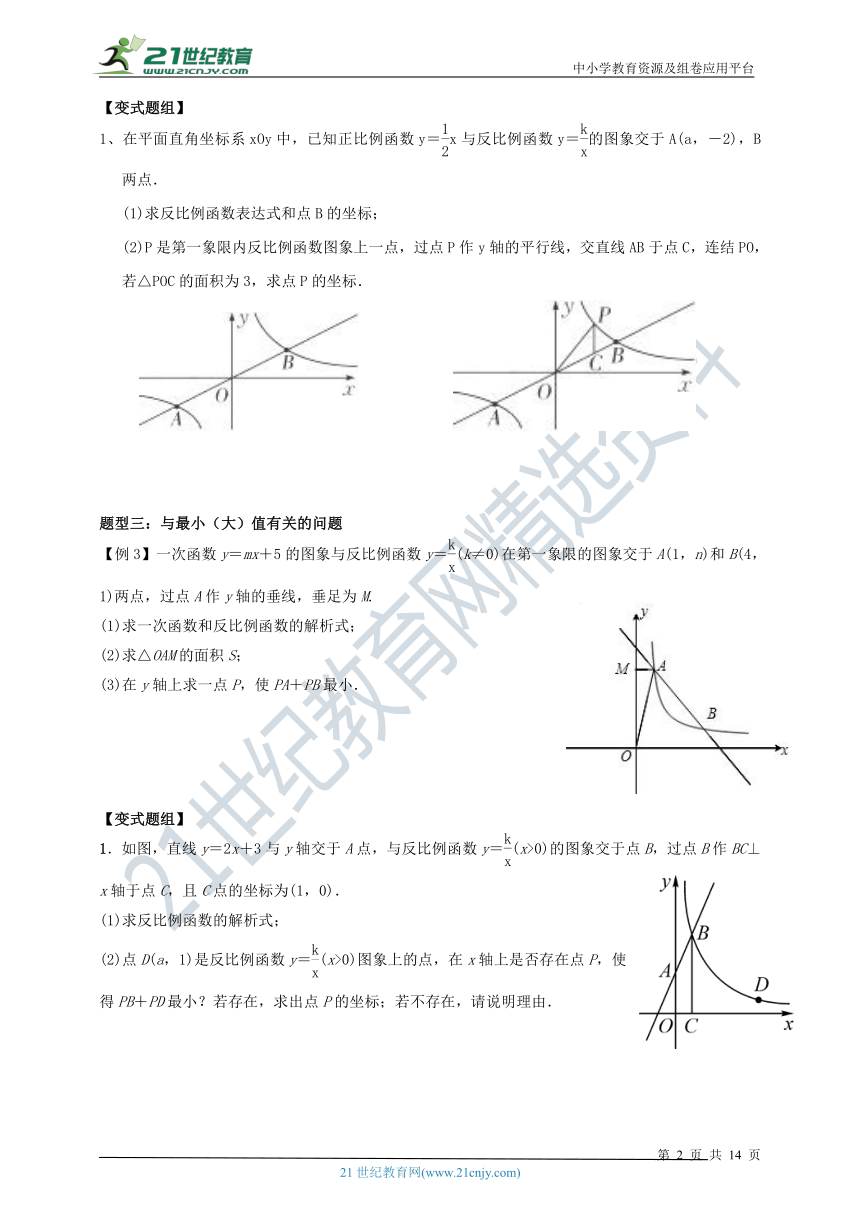
1、在平面直角坐标系xOy中,已知正比例函数y=x与反比例函数y=的图象交于A(a,-2),B两点.
(1)求反比例函数表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连结PO,若△POC的面积为3,求点P的坐标.
题型三:与最小(大)值有关的问题
【例3】一次函数y=mx+5的图象与反比例函数y=(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.
(1)求一次函数和反比例函数的解析式;
(2)求△OAM的面积S;
(3)在y轴上求一点P,使PA+PB最小.
【变式题组】
1.如图,直线y=2x+3与y轴交于A点,与反比例函数y=(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
题型四:与面积有关的动点或存在问题
【例4】如图,反比例函数的图象与一次函数的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1)
(1)求反比例函数与一次函数的表达式。
(2)点E为y轴上的一个动点,若,求点E的坐标
【变式题组】
如图,正比例函数y=2x的图象与反比例函数y=的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
演练巩固·培优升级
1、一次函数y1=ax+b与反比例函数y2=(k≠0)在同一直角坐标系中的图象如图,则当y1<y2时,x的取值范围是____.
2、函数y1=x与y2=的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是_______.
3、如图,一次函数y=kx-1的图象与x轴交于点A,与反比例函数y=(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是_______.21教育网
4、如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=(x>0)的图象上,已知点B的坐标是,则k的值为(
)
A.4
B.6
C.8
D.10
5、如图,A,B两点在反比例函数y=的图像上,C,D两点分别在反比例函数y=的图像上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1-k2的值是
(
)
A.6
B.4
C.3
D.2
6、一次函数与反比例函数,其中,a、b为常数,它们在同一坐标系中的图象可以是(
)
7、如图,一次函数()与反比例函数()的图象交于点A(﹣1,2),B(m,﹣1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.
8、如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与x轴,y轴分别交于A,B两点,且与反比例函数y=(n为常数且n≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的表达式;
(2)求两函数图象的另一个交点的坐标;
(3)直接写出不等式kx+b≤的解集.
.
第九讲
一次函数与反比例函数之专题突破培优答案
在历年中考试题中一次函数和反比例函数常以综合题形式出现,这类试题不仅能考查两个函数的基本性质,而且能考查同学们综合分析问题的能力。现以以下典型例题为例,浅谈这类问题的解法,供参考。
典型例题
题型一:求同一坐标系下的图象
【例1】
已知函数与在同一直角坐标系中的图象大致如图1,则下列结论正确的是(
B
)
A.
B.
C.
D.
【变式题组】
1、在同一直角坐标系中,函数与的图象大致是(
C
)
A.
B.
C.
D.
2、当k>0时,反比例函数和一次函数的图象大致是(
C
)
题型二:一次函数与反比例函数结合求解析式,自变量的取值范围,面积等
【例2】如图,已知,是一次函数的图象和反比例函数的图象的两个交点.www-2-1-cnjy-com
(1)求一次函数、反比例函数的关系式;
(2)求△AOB的面积.
(3)当自变量x满足什么条件时,y1>y2
.(直接写出答案)
(4)将反比例函数的图象向右平移n(n>0)个单位,得到的新图象经过点(3,-4),求对应的函数关系式y3.(直接写出答案)2-1-c-n-j-y
分析:(1)、将B点坐标代入反比例函数解析式可得,将A点代入可得点A的坐标为(-4,2),将A、B两点代入一次函数解析式可得一次函数解析式为y=-x-2.
(2)、根据题意可得C(-2,0)
S=2×2÷2+2×4÷2=2+4=6
(3)、根据图形可得x<-4或0<x<2
(4)y3=
【答案】(1)、;y=-x-2;(2)、S=6;(3)、x<-4或0<x<2;(4)、y3=
【变式题组】
1、在平面直角坐标系xOy中,已知正比例函数y=x与反比例函数y=的图象交于A(a,-2),B两点.21教育网
(1)求反比例函数表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连结PO,若△POC的面积为3,求点P的坐标.
【答案】解:(1)把A(a,﹣2)代入y=x,可得a=﹣4,
∴A(﹣4,﹣2),
把A(﹣4,﹣2)代入y=,可得k=8,
∴反比例函数的表达式为y=,
∵点B与点A关于原点对称,
∴B(4,2);
(2)如图所示,过P作PE⊥x轴于E,交AB于C,
设P(m,),则C(m,m),
∵△POC的面积为3,
∴m×|m﹣|=3,
解得m=2或2,
∴P(2,)或(2,4).
题型三:与最小(大)值有关的问题
【例3】一次函数y=mx+5的图象与反比例函数y=(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.
(1)求一次函数和反比例函数的解析式;
(2)求△OAM的面积S;
(3)在y轴上求一点P,使PA+PB最小.
解(1)将B(4,1)代入y=,k=4,所
将A(1,4),B(4,1)代入y=mx+5,∴y=-x+5,(4分)
(2)在中,令x=1,解得y=4,∴A(1,4)∴S=×1×4=2,
(3)作点A关于y轴的对称点N,则N(-1,4),
连接BN交y轴于点P,点P即为所求.
设直线BN的关系式为y=kx+b,
把B(4,1),N(-1,4)代入得y=
∴
【变式题组】
1.如图,直线y=2x+3与y轴交于A点,与反比例函数y=(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)∵BC⊥x轴于点C,且C点的坐标为(1,0),
∴在直线y=2x+3中,当x=1时,y=2+3=5,
∴点B的坐标为(1,5),
又∵点B(1,5)在反比例函数y=上,∴k=1×5=5,
∴反比例函数的解析式为:y=
(2)将点D(a,1)代入y=,得:a=5,
∴点D坐标为(5,1)
设点D(5,1)关于x轴的对称点为D′(5,-1),
过点B(1,5)、点D′(5,-1)的直线解析式为:y=kx+b,
可∴直线BD′的解析式为:y=-
根据题意知,直线BD′与x轴的交点即为所求点P,
当y=0时,得:=0解得:x=
故点P的坐标为(,0)
题型四:与与面积有关的动点或存在问题
【例4】如图,反比例函数的图象与一次函数的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1)
(1)求反比例函数与一次函数的表达式。
(2)点E为y轴上的一个动点,若,求点E的坐标
解:(1)Y=,
(2)点E的坐标(0,5),(0,9)
【变式题组】
如图,正比例函数y=2x的图象与反比例函数y=的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
解:(1)∵反比例函数与正比例函数的图象相交于A、B两点,
∴A、B两点关于原点对称,∴OA=OB,
∴△BOC的面积=△AOC的面积=2÷2=1,
又∵A是反比例函数y=
图象上的点,且AC⊥x轴于点C,
∴△AOC的面积==1,∵k>0,∴k=2.
故这个反比例函数的解析式为y=;
(2)x轴上存在一点D,使△ABD为直角三角形.设D(m,0)
将y=2x与y=
联立成方程组得交点坐标:A(1,2),B(-1,-2),
AD =(1-m) +2 ,
BD =(1+m) +2 ,
AB =(1+1) +(2+2) =20
①当AD⊥AB时,如图1,BD =AB +AD ,解得m=5∴D(5,0);
②当BD⊥AB时,如图2,AD =AB +BD ,解得m=-5∴D(-5,0);
③当AD⊥BD时,如图3,BA =DB +AD ,解得m=∴D(
,0).
故x轴上存在一点D,使△ABD为直角三角形,点D的坐标为(5,0)或(-5,0)或(
,0)
演练巩固·培优升级
1、一次函数y1=ax+b与反比例函数y2=(k≠0)在同一直角坐标系中的图象如图,则当y1<y2时,x的取值范围是_-13___.
2.(2017,南京)函数y1=x与y2=的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是____①_③___.
3、如图,一次函数y=kx-1的图象与x轴交于点A,与反比例函数y=(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是___2_____.
4、如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=(x>0)的图象上,已知点B的坐标是,则k的值为( C )
A.4
B.6
C.8
D.10
5、如图,A,B两点在反比例函数y=的图像上,C,D两点分别在反比例函数y=的图像上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1-k2的值是
( D )
A.6
B.4
C.3
D.2
6、一次函数与反比例函数,其中,a、b为常数,它们在同一坐标系中的图象可以是(
C
)
7、如图,一次函数()与反比例函数()的图象交于点A(﹣1,2),B(m,﹣1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.
分析:
(1)利用待定系数法即可解决问题;
(2)分三种情形讨论:①PA=PB,②
AP=AB,③BP=BA.分别解方程即可解决问题;
【答案】(1),y=﹣x+1;(2)n=或.
【解析】(1)把A(﹣1,2)代入,得到k2=﹣2,∴反比例函数的解析式为.
∵B(m,﹣1)在上,∴m=2,由题意得:,解得:,∴一次函数的解析式为y=﹣x+1.
(2)∵A(﹣1,2),B(2,﹣1),∴AB=,分三种情况讨论:
①当PA=PB时,(n+1)2+4=(n﹣2)2+1,∴n=0,∵n>0,∴n=0不合题意舍弃.
②当AP=AB时,22+(n+1)2=()2,∵n>0,∴n=﹣1+.
③当BP=BA时,12+(n﹣2)2=()2,∵n>0,∴n=2+.
综上所述,n=或.
8、如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与x轴,y轴分别交于A,B两点,且与反比例函数y=(n为常数且n≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=6.21世纪教育网版权所有
(1)求一次函数与反比例函数的表达式;
(2)求两函数图象的另一个交点的坐标;
(3)直接写出不等式kx+b≤的解集.
答案:
解:(1)∵OB=2OA=3OD=6,
∴OB=6,OA=3,OD=2,
∵CD⊥DA,∴DC∥OB,
∴=,∴=,
∴DC=10,
∴C(-2,10),B(0,6),A(3,0),
代入一次函数y=kx+b,
得解得
∴一次函数的表达式为y=-2x+6.
∵反比例函数y=经过点C(-2,10),
∴n=-20,
∴反比例函数的表达式为y=-;
(2)由解得或
∴另一个交点坐标为(5,-4);
(3)由图象可知kx+b≤的解集为-2≤x<0或x≥5.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第九讲
一次函数与反比例函数之专题突破培优辅导
在历年中考试题中一次函数和反比例函数常以综合题形式出现,这类试题不仅能考查两个函数的基本性质,而且能考查同学们综合分析问题的能力。现以以下典型例题为例,浅谈这类问题的解法,供参考。
典型例题
题型一:求同一坐标系下的图象
【例1】
已知函数与在同一直角坐标系中的图象大致如图1,则下列结论正确的是(
)
A.
B.
C.
D.
【变式题组】
1、在同一直角坐标系中,函数与的图象大致是(
)
A.
B.
C.
D.
2、当k>0时,反比例函数和一次函数的图象大致是(
)
题型二:一次函数与反比例函数结合求解析式,自变量的取值范围,面积等
【例2】如图,已知,是一次函数的图象和反比例函数的图象的两个交点.www-2-1-cnjy-com
(1)求一次函数、反比例函数的关系式;
(2)求△AOB的面积.
(3)当自变量x满足什么条件时,y1>y2
.(直接写出答案)
(4)将反比例函数的图象向右平移n(n>0)个单位,得到的新图象经过点(3,-4),求对应的函数关系式y3.(直接写出答案)2-1-c-n-j-y
【变式题组】
1、在平面直角坐标系xOy中,已知正比例函数y=x与反比例函数y=的图象交于A(a,-2),B两点.
(1)求反比例函数表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连结PO,若△POC的面积为3,求点P的坐标.
题型三:与最小(大)值有关的问题
【例3】一次函数y=mx+5的图象与反比例函数y=(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.
(1)求一次函数和反比例函数的解析式;
(2)求△OAM的面积S;
(3)在y轴上求一点P,使PA+PB最小.
【变式题组】
1.如图,直线y=2x+3与y轴交于A点,与反比例函数y=(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
题型四:与面积有关的动点或存在问题
【例4】如图,反比例函数的图象与一次函数的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1)
(1)求反比例函数与一次函数的表达式。
(2)点E为y轴上的一个动点,若,求点E的坐标
【变式题组】
如图,正比例函数y=2x的图象与反比例函数y=的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
演练巩固·培优升级
1、一次函数y1=ax+b与反比例函数y2=(k≠0)在同一直角坐标系中的图象如图,则当y1<y2时,x的取值范围是____.
2、函数y1=x与y2=的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是_______.
3、如图,一次函数y=kx-1的图象与x轴交于点A,与反比例函数y=(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是_______.21教育网
4、如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=(x>0)的图象上,已知点B的坐标是,则k的值为(
)
A.4
B.6
C.8
D.10
5、如图,A,B两点在反比例函数y=的图像上,C,D两点分别在反比例函数y=的图像上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1-k2的值是
(
)
A.6
B.4
C.3
D.2
6、一次函数与反比例函数,其中,a、b为常数,它们在同一坐标系中的图象可以是(
)
7、如图,一次函数()与反比例函数()的图象交于点A(﹣1,2),B(m,﹣1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.
8、如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与x轴,y轴分别交于A,B两点,且与反比例函数y=(n为常数且n≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的表达式;
(2)求两函数图象的另一个交点的坐标;
(3)直接写出不等式kx+b≤的解集.
.
第九讲
一次函数与反比例函数之专题突破培优答案
在历年中考试题中一次函数和反比例函数常以综合题形式出现,这类试题不仅能考查两个函数的基本性质,而且能考查同学们综合分析问题的能力。现以以下典型例题为例,浅谈这类问题的解法,供参考。
典型例题
题型一:求同一坐标系下的图象
【例1】
已知函数与在同一直角坐标系中的图象大致如图1,则下列结论正确的是(
B
)
A.
B.
C.
D.
【变式题组】
1、在同一直角坐标系中,函数与的图象大致是(
C
)
A.
B.
C.
D.
2、当k>0时,反比例函数和一次函数的图象大致是(
C
)
题型二:一次函数与反比例函数结合求解析式,自变量的取值范围,面积等
【例2】如图,已知,是一次函数的图象和反比例函数的图象的两个交点.www-2-1-cnjy-com
(1)求一次函数、反比例函数的关系式;
(2)求△AOB的面积.
(3)当自变量x满足什么条件时,y1>y2
.(直接写出答案)
(4)将反比例函数的图象向右平移n(n>0)个单位,得到的新图象经过点(3,-4),求对应的函数关系式y3.(直接写出答案)2-1-c-n-j-y
分析:(1)、将B点坐标代入反比例函数解析式可得,将A点代入可得点A的坐标为(-4,2),将A、B两点代入一次函数解析式可得一次函数解析式为y=-x-2.
(2)、根据题意可得C(-2,0)
S=2×2÷2+2×4÷2=2+4=6
(3)、根据图形可得x<-4或0<x<2
(4)y3=
【答案】(1)、;y=-x-2;(2)、S=6;(3)、x<-4或0<x<2;(4)、y3=
【变式题组】
1、在平面直角坐标系xOy中,已知正比例函数y=x与反比例函数y=的图象交于A(a,-2),B两点.21教育网
(1)求反比例函数表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连结PO,若△POC的面积为3,求点P的坐标.
【答案】解:(1)把A(a,﹣2)代入y=x,可得a=﹣4,
∴A(﹣4,﹣2),
把A(﹣4,﹣2)代入y=,可得k=8,
∴反比例函数的表达式为y=,
∵点B与点A关于原点对称,
∴B(4,2);
(2)如图所示,过P作PE⊥x轴于E,交AB于C,
设P(m,),则C(m,m),
∵△POC的面积为3,
∴m×|m﹣|=3,
解得m=2或2,
∴P(2,)或(2,4).
题型三:与最小(大)值有关的问题
【例3】一次函数y=mx+5的图象与反比例函数y=(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.
(1)求一次函数和反比例函数的解析式;
(2)求△OAM的面积S;
(3)在y轴上求一点P,使PA+PB最小.
解(1)将B(4,1)代入y=,k=4,所
将A(1,4),B(4,1)代入y=mx+5,∴y=-x+5,(4分)
(2)在中,令x=1,解得y=4,∴A(1,4)∴S=×1×4=2,
(3)作点A关于y轴的对称点N,则N(-1,4),
连接BN交y轴于点P,点P即为所求.
设直线BN的关系式为y=kx+b,
把B(4,1),N(-1,4)代入得y=
∴
【变式题组】
1.如图,直线y=2x+3与y轴交于A点,与反比例函数y=(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)∵BC⊥x轴于点C,且C点的坐标为(1,0),
∴在直线y=2x+3中,当x=1时,y=2+3=5,
∴点B的坐标为(1,5),
又∵点B(1,5)在反比例函数y=上,∴k=1×5=5,
∴反比例函数的解析式为:y=
(2)将点D(a,1)代入y=,得:a=5,
∴点D坐标为(5,1)
设点D(5,1)关于x轴的对称点为D′(5,-1),
过点B(1,5)、点D′(5,-1)的直线解析式为:y=kx+b,
可∴直线BD′的解析式为:y=-
根据题意知,直线BD′与x轴的交点即为所求点P,
当y=0时,得:=0解得:x=
故点P的坐标为(,0)
题型四:与与面积有关的动点或存在问题
【例4】如图,反比例函数的图象与一次函数的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1)
(1)求反比例函数与一次函数的表达式。
(2)点E为y轴上的一个动点,若,求点E的坐标
解:(1)Y=,
(2)点E的坐标(0,5),(0,9)
【变式题组】
如图,正比例函数y=2x的图象与反比例函数y=的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
解:(1)∵反比例函数与正比例函数的图象相交于A、B两点,
∴A、B两点关于原点对称,∴OA=OB,
∴△BOC的面积=△AOC的面积=2÷2=1,
又∵A是反比例函数y=
图象上的点,且AC⊥x轴于点C,
∴△AOC的面积==1,∵k>0,∴k=2.
故这个反比例函数的解析式为y=;
(2)x轴上存在一点D,使△ABD为直角三角形.设D(m,0)
将y=2x与y=
联立成方程组得交点坐标:A(1,2),B(-1,-2),
AD =(1-m) +2 ,
BD =(1+m) +2 ,
AB =(1+1) +(2+2) =20
①当AD⊥AB时,如图1,BD =AB +AD ,解得m=5∴D(5,0);
②当BD⊥AB时,如图2,AD =AB +BD ,解得m=-5∴D(-5,0);
③当AD⊥BD时,如图3,BA =DB +AD ,解得m=∴D(
,0).
故x轴上存在一点D,使△ABD为直角三角形,点D的坐标为(5,0)或(-5,0)或(
,0)
演练巩固·培优升级
1、一次函数y1=ax+b与反比例函数y2=(k≠0)在同一直角坐标系中的图象如图,则当y1<y2时,x的取值范围是_-1
2.(2017,南京)函数y1=x与y2=的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是____①_③___.
3、如图,一次函数y=kx-1的图象与x轴交于点A,与反比例函数y=(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是___2_____.
4、如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=(x>0)的图象上,已知点B的坐标是,则k的值为( C )
A.4
B.6
C.8
D.10
5、如图,A,B两点在反比例函数y=的图像上,C,D两点分别在反比例函数y=的图像上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1-k2的值是
( D )
A.6
B.4
C.3
D.2
6、一次函数与反比例函数,其中,a、b为常数,它们在同一坐标系中的图象可以是(
C
)
7、如图,一次函数()与反比例函数()的图象交于点A(﹣1,2),B(m,﹣1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.
分析:
(1)利用待定系数法即可解决问题;
(2)分三种情形讨论:①PA=PB,②
AP=AB,③BP=BA.分别解方程即可解决问题;
【答案】(1),y=﹣x+1;(2)n=或.
【解析】(1)把A(﹣1,2)代入,得到k2=﹣2,∴反比例函数的解析式为.
∵B(m,﹣1)在上,∴m=2,由题意得:,解得:,∴一次函数的解析式为y=﹣x+1.
(2)∵A(﹣1,2),B(2,﹣1),∴AB=,分三种情况讨论:
①当PA=PB时,(n+1)2+4=(n﹣2)2+1,∴n=0,∵n>0,∴n=0不合题意舍弃.
②当AP=AB时,22+(n+1)2=()2,∵n>0,∴n=﹣1+.
③当BP=BA时,12+(n﹣2)2=()2,∵n>0,∴n=2+.
综上所述,n=或.
8、如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与x轴,y轴分别交于A,B两点,且与反比例函数y=(n为常数且n≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=6.21世纪教育网版权所有
(1)求一次函数与反比例函数的表达式;
(2)求两函数图象的另一个交点的坐标;
(3)直接写出不等式kx+b≤的解集.
答案:
解:(1)∵OB=2OA=3OD=6,
∴OB=6,OA=3,OD=2,
∵CD⊥DA,∴DC∥OB,
∴=,∴=,
∴DC=10,
∴C(-2,10),B(0,6),A(3,0),
代入一次函数y=kx+b,
得解得
∴一次函数的表达式为y=-2x+6.
∵反比例函数y=经过点C(-2,10),
∴n=-20,
∴反比例函数的表达式为y=-;
(2)由解得或
∴另一个交点坐标为(5,-4);
(3)由图象可知kx+b≤的解集为-2≤x<0或x≥5.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
