人教版八年级下册 18.1.1 平行四边形的性质课件(23张PPT)
文档属性
| 名称 | 人教版八年级下册 18.1.1 平行四边形的性质课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-21 19:36:52 | ||
图片预览

文档简介
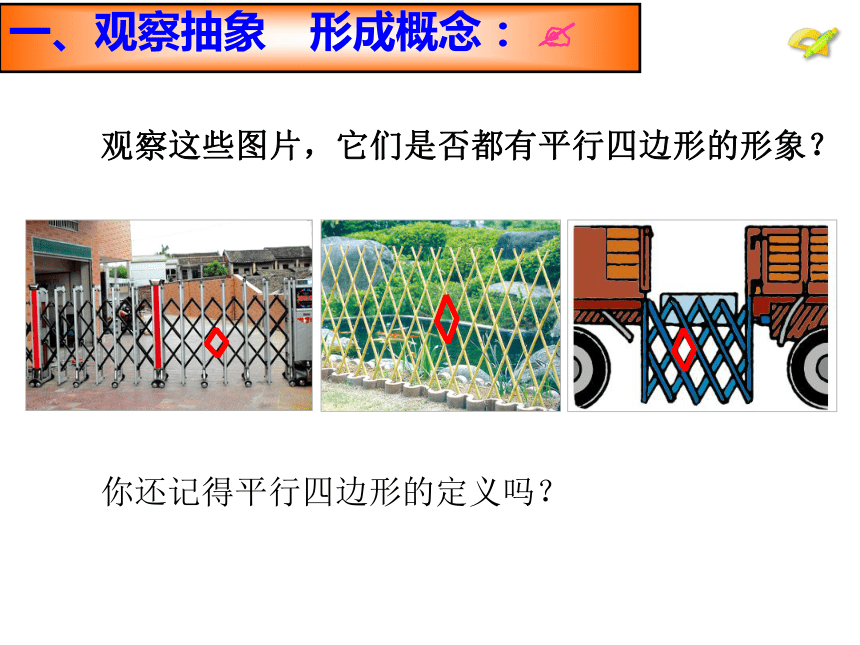
课件23张PPT。18.1.1平行四边形的性质 观察这些图片,它们是否都有平行四边形的形象? 你还记得平行四边形的定义吗?
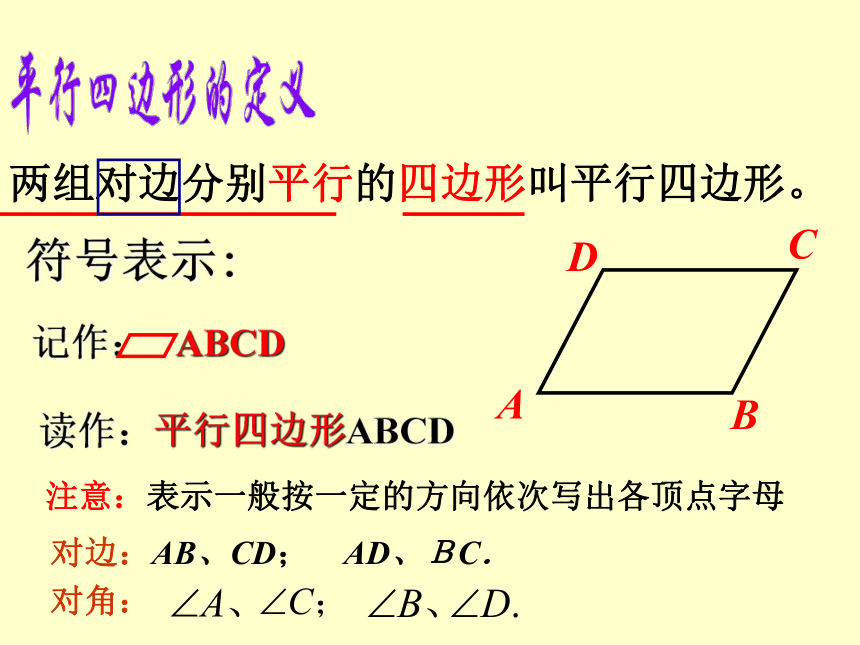
一、观察抽象 形成概念: ? 两组对边分别平行的四边形叫平行四边形。符号表示:记作: ABCD读作:平行四边形ABCDDCAB对边:AB、CD; AD、BC.
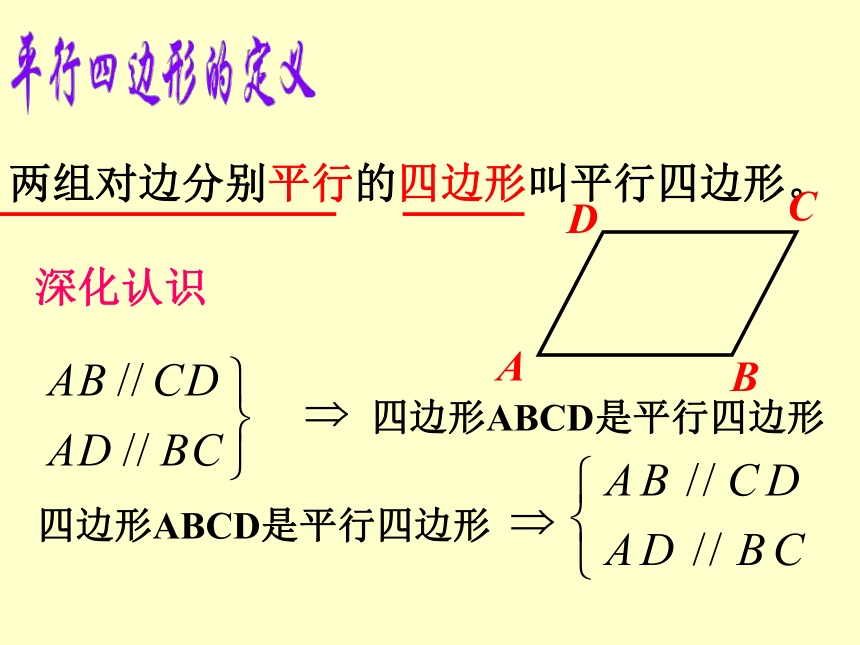
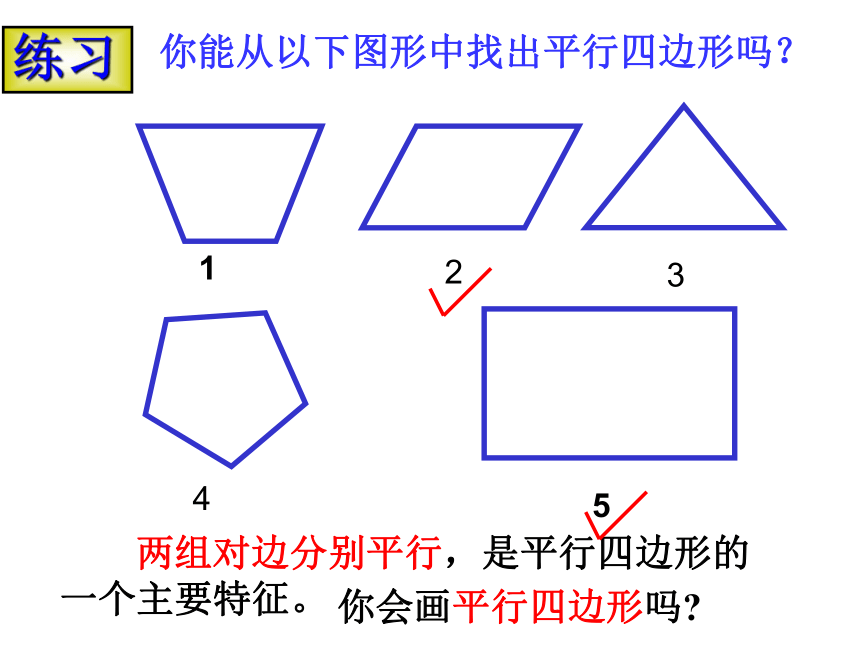
对角: 注意:表示一般按一定的方向依次写出各顶点字母两组对边分别平行的四边形叫平行四边形。DCAB四边形ABCD是平行四边形四边形ABCD是平行四边形深化认识你能从以下图形中找出平行四边形吗? 两组对边分别平行,是平行四边形的一个主要特征。23145你会画平行四边形吗?练习
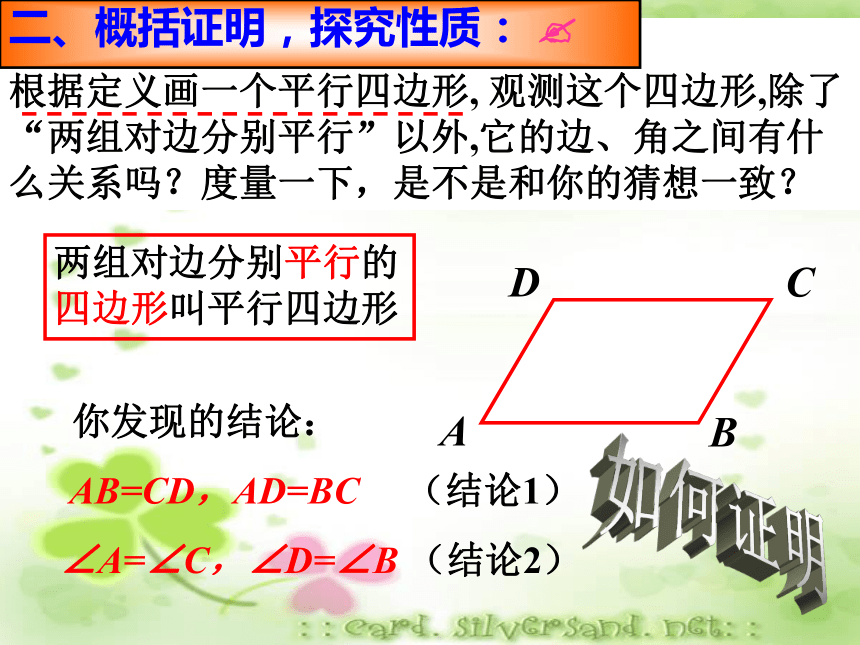
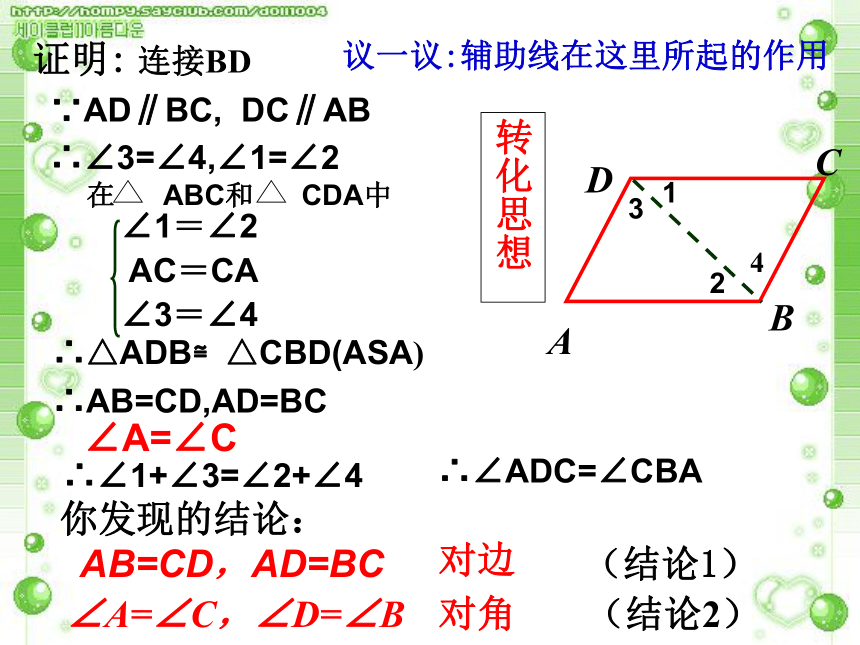
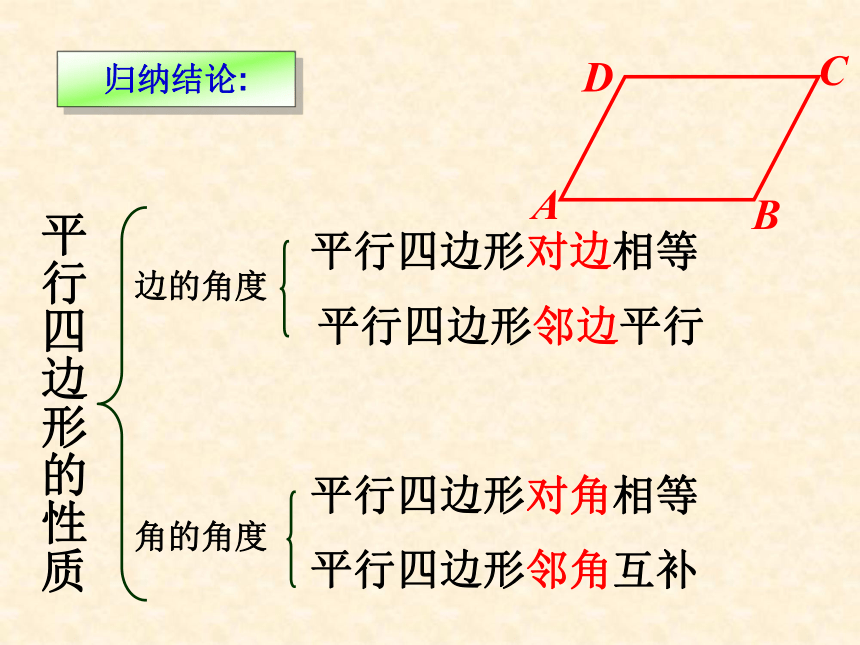
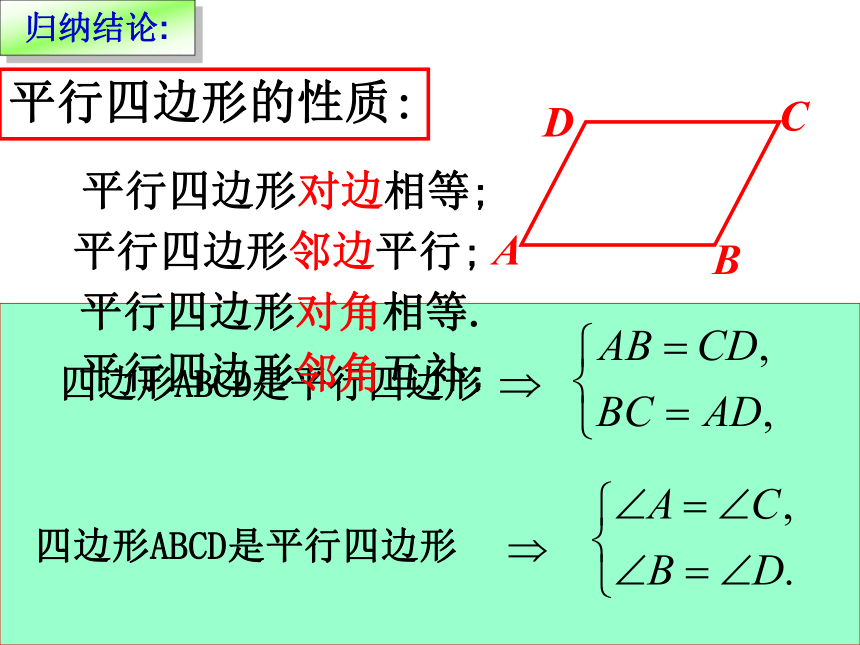
根据定义画一个平行四边形, 观测这个四边形,除了“两组对边分别平行”以外,它的边、角之间有什么关系吗?度量一下,是不是和你的猜想一致?你发现的结论:AB=CD,AD=BC (结论1) ∠A=∠C,∠D=∠B (结论2) 两组对边分别平行的四边形叫平行四边形如何证明二、概括证明,探究性质: ? 你发现的结论:AB=CD,AD=BC (结论1) ∠A=∠C,∠D=∠B (结论2) 证明:连接BD∵AD∥BC, DC∥AB∴∠3=∠4,∠1=∠2∴△ADB≌△CBD(ASA)∴AB=CD,AD=BC∠A=∠C∴∠1+∠3=∠2+∠4∴∠ADC=∠CBA对边对角转化思想议一议:辅助线在这里所起的作用DCA BDCAB归纳结论: 平行四边形对边相等平行四边形对角相等平行四边形邻边平行平行四边形邻角互补平行四边形的性质边的角度角的角度四边形ABCD是平行四边形DCAB归纳结论: 平行四边形对边相等;平行四边形对角相等.平行四边形的性质:平行四边形邻边平行;平行四边形邻角互补;三、应用知识,解决问题: ? 840°练习证明:∵四边形ABCD是平行四边形,∴∠A=∠C,AD=CB,∵DE⊥AB,BF⊥CD,∴∠AED=∠CFD=90°∴ AE=CF例1DE=BF吗?HABCDG两条平行线之间的平行线段相等ba猜 一 猜 如图,若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B,则GH、AD 、BC的长短相等吗?为什么?∟∟∟ 如图,若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.则GH、AD 、BC的长短相等吗?为什么?一条直线上的任一点到另一条直线的距离,叫做这两条平行线间的距离。两条平行线间的距离相等 点与点之间距离,点与直线之间距离,直线与直线之间距离的联系与区别?
议一议距离
点与点的
距离
点与直线
的距离
两条平行线
的距离概念
图形
(两点之间线段最短)
连结两点直间线段的长度
直线外一点到这条直线的垂线
段的长度
(连接直线外一点与直线上
各点的所有线段中,垂线段最短)
一条直线上的任一点到另一条
直线的距离
(两条平行线上点与点之
间最短路径的长度)
BDDCABDC练习1.在 ABCD中,若∠B=70°,则∠D=( )E五、目标检测题? 5. 已知:如图, AD∥BC,AE∥CD,BD平分∠ABC ,求证:AB=CE.3五、目标检测题? 有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?实际问题学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?A1A3A2学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?拓广提高 如图,△ABC是等腰三角形,P是底边BC上一动点,且PE //AB,PF //AC,求证:PE+PF=AB.本节课我们有哪些收获?一.平行四边形的性质:二. 数学思想:体验数学学习的过程:观察、猜测、归纳、证明、运用1.平行四边形对边相等;2.平行四边形对角相等.3.平行四边形
对边平行;化归思想课堂小结 ? 测量、作业:1、教科书第43页练习第1,2题;
习题18.1第1,2,7,8题.
2、练习册,平行四边形的性质,第1课时
课后作业
一、观察抽象 形成概念: ? 两组对边分别平行的四边形叫平行四边形。符号表示:记作: ABCD读作:平行四边形ABCDDCAB对边:AB、CD; AD、BC.
对角: 注意:表示一般按一定的方向依次写出各顶点字母两组对边分别平行的四边形叫平行四边形。DCAB四边形ABCD是平行四边形四边形ABCD是平行四边形深化认识你能从以下图形中找出平行四边形吗? 两组对边分别平行,是平行四边形的一个主要特征。23145你会画平行四边形吗?练习
根据定义画一个平行四边形, 观测这个四边形,除了“两组对边分别平行”以外,它的边、角之间有什么关系吗?度量一下,是不是和你的猜想一致?你发现的结论:AB=CD,AD=BC (结论1) ∠A=∠C,∠D=∠B (结论2) 两组对边分别平行的四边形叫平行四边形如何证明二、概括证明,探究性质: ? 你发现的结论:AB=CD,AD=BC (结论1) ∠A=∠C,∠D=∠B (结论2) 证明:连接BD∵AD∥BC, DC∥AB∴∠3=∠4,∠1=∠2∴△ADB≌△CBD(ASA)∴AB=CD,AD=BC∠A=∠C∴∠1+∠3=∠2+∠4∴∠ADC=∠CBA对边对角转化思想议一议:辅助线在这里所起的作用DCA BDCAB归纳结论: 平行四边形对边相等平行四边形对角相等平行四边形邻边平行平行四边形邻角互补平行四边形的性质边的角度角的角度四边形ABCD是平行四边形DCAB归纳结论: 平行四边形对边相等;平行四边形对角相等.平行四边形的性质:平行四边形邻边平行;平行四边形邻角互补;三、应用知识,解决问题: ? 840°练习证明:∵四边形ABCD是平行四边形,∴∠A=∠C,AD=CB,∵DE⊥AB,BF⊥CD,∴∠AED=∠CFD=90°∴ AE=CF例1DE=BF吗?HABCDG两条平行线之间的平行线段相等ba猜 一 猜 如图,若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B,则GH、AD 、BC的长短相等吗?为什么?∟∟∟ 如图,若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.则GH、AD 、BC的长短相等吗?为什么?一条直线上的任一点到另一条直线的距离,叫做这两条平行线间的距离。两条平行线间的距离相等 点与点之间距离,点与直线之间距离,直线与直线之间距离的联系与区别?
议一议距离
点与点的
距离
点与直线
的距离
两条平行线
的距离概念
图形
(两点之间线段最短)
连结两点直间线段的长度
直线外一点到这条直线的垂线
段的长度
(连接直线外一点与直线上
各点的所有线段中,垂线段最短)
一条直线上的任一点到另一条
直线的距离
(两条平行线上点与点之
间最短路径的长度)
BDDCABDC练习1.在 ABCD中,若∠B=70°,则∠D=( )E五、目标检测题? 5. 已知:如图, AD∥BC,AE∥CD,BD平分∠ABC ,求证:AB=CE.3五、目标检测题? 有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?实际问题学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?A1A3A2学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?拓广提高 如图,△ABC是等腰三角形,P是底边BC上一动点,且PE //AB,PF //AC,求证:PE+PF=AB.本节课我们有哪些收获?一.平行四边形的性质:二. 数学思想:体验数学学习的过程:观察、猜测、归纳、证明、运用1.平行四边形对边相等;2.平行四边形对角相等.3.平行四边形
对边平行;化归思想课堂小结 ? 测量、作业:1、教科书第43页练习第1,2题;
习题18.1第1,2,7,8题.
2、练习册,平行四边形的性质,第1课时
课后作业
