第5章 生活中的轴对称单元检测试卷A

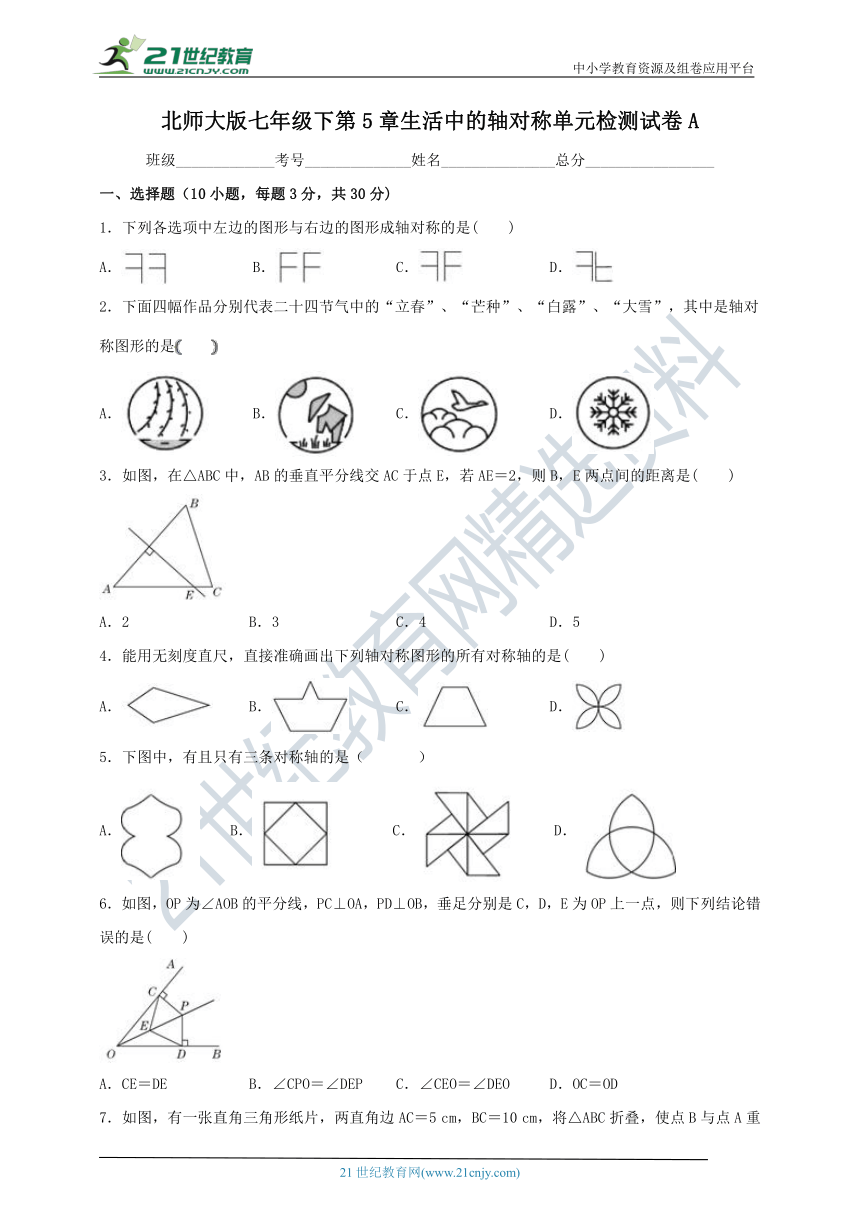
北师大版七年级下第5章生活中的轴对称单元检测试卷A
班级_____________考号______________姓名_______________总分_________________
一、选择题（10小题，每题3分，共30分)
1．下列各选项中左边的图形与右边的图形成轴对称的是(　　)
A． B． C． D．
2．下面四幅作品分别代表二十四节气中的“立春”、“芒种”、“白露”、“大雪”，其中是轴对称图形的是　　
A． B． C． D．
3．如图，在△ABC中，AB的垂直平分线交AC于点E，若AE＝2，则B，E两点间的距离是(　　)
A．2 B．3 C．4 D．5
4．能用无刻度直尺，直接准确画出下列轴对称图形的所有对称轴的是(　　)
A． B． C． D．
5．下图中，有且只有三条对称轴的是（??? ）
A． B． C． D．
6．如图，OP为∠AOB的平分线，PC⊥OA，PD⊥OB，垂足分别是C，D，E为OP上一点，则下列结论错误的是(　　)
A．CE＝DE B．∠CPO＝∠DEP C．∠CEO＝∠DEO D．OC＝OD
7．如图，有一张直角三角形纸片，两直角边AC＝5 cm，BC＝10 cm，将△ABC折叠，使点B与点A重合，折痕为DE，则△ACD的周长为(　　)
A．10cm B．12cm C．15cm D．20cm
8．已知等腰三角形的底角是35°，则它的顶角是（ ）
A．70° B．100° C．110° D．130°
9．下列说法：
①两边和其中一边的对角对应相等的两个三角形全等．
②角的对称轴是角平分线
③两边对应相等的两直角三角形全等
④成轴对称的两图形一定全等
⑤到线段两端距离相等的点在线段的垂直平分线上，
正确的有（　　）个．
A．2 B．3 C．4 D．5
10．如图，在△ABC中，AB=AC，∠A =36°，AB的垂直平分线DE交AC于点D，交AB于点E．有下列结论：①BD平分∠ABC；②AD=BD=BC；③△BCD的周长等于AB+BC；④D是AC的中点．其中正确的有（ ）
A．1个 B．2个 C．3个 D．4个
二、填空题（8小题，每题3分，共24分)
11．已知等腰三角形的顶角是底角的4倍，则顶角的度数为_____．
12．如图所示，AD是△ABC的角平分线，△ABC的一个外角的平分线AE交边BC的延长线于点E，且∠BAD＝20°，∠E＝30°，则∠B的度数为________．
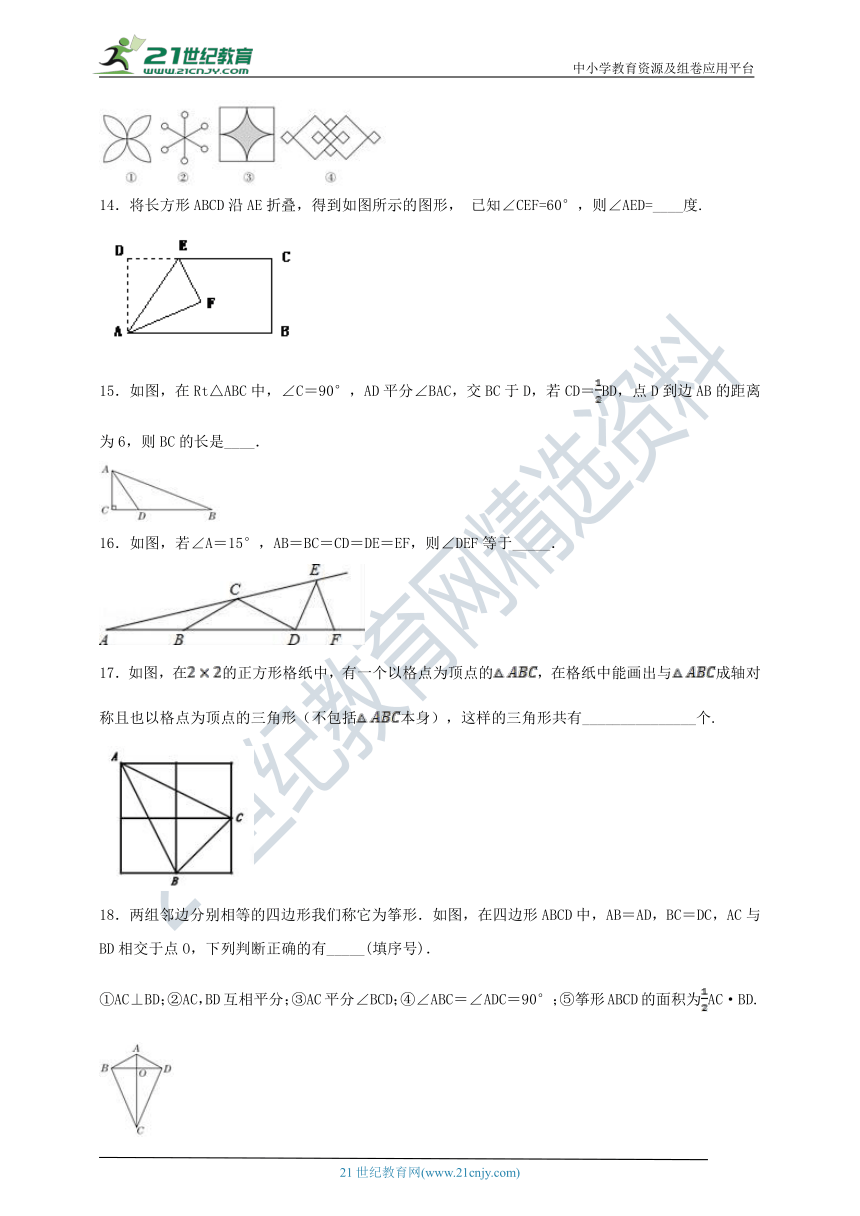
13．以下图形中，对称轴的条数大于3的有____个．
14．将长方形ABCD沿AE折叠，得到如图所示的图形， 已知∠CEF=60°，则∠AED=____度.
15．如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC，交BC于D，若CD＝BD，点D到边AB的距离为6，则BC的长是____．
16．如图，若∠A＝15°，AB＝BC＝CD＝DE＝EF，则∠DEF等于_____．
17．如图，在的正方形格纸中，有一个以格点为顶点的，在格纸中能画出与成轴对称且也以格点为顶点的三角形（不包括本身），这样的三角形共有_______________个.
18．两组邻边分别相等的四边形我们称它为筝形．如图，在四边形ABCD中，AB＝AD，BC＝DC，AC与BD相交于点O，下列判断正确的有_____(填序号)．
①AC⊥BD；②AC，BD互相平分；③AC平分∠BCD；④∠ABC＝∠ADC＝90°；⑤筝形ABCD的面积为AC·BD.
三、解答题（8小题，共66分)
19．把图中的图形补成轴对称图形，其中MN，EF为各图形的对称轴．
20．如图，已知△ABC是等腰三角形，且AB＝AC，D是△ABC外部的一点，连接AD，BD.已知AB＝AD，AD∥BC，∠D＝35°，求∠DAC的度数．
21．如图，D为△ABC边BC延长线上一点，且CD＝CA，E是AD的中点，CF平分∠ACB交AB于点F，试判断CE与CF的位置关系．
22．如图，在△ABC中，∠C＝90°，AB的垂直平分线交BC于点D，交AB于点E，∠DAE与∠DAC的度数比为2∶1，求∠B的度数．
23．如图，校园有两条路OA、OB，在交叉口附近有两块宣传牌C、D，学校准备在这里安装一盏路灯，要求灯柱的位置P离两块宣传牌一样远，并且到两条路的距离也一样远，请你用直尺和圆规画出灯柱的位置点P．（不写作图步骤，保留作图痕迹）
24．如图，在四边形ABCD中，AC⊥BD于点E，BE＝DE，已知AC＝10 cm，BD＝8 cm，求阴影部分的面积．
25．如图，△ABC是等腰直角三角形，AB＝BC，O是△ABC内部的一个动点，△OBD是等腰直角三角形，OB＝BD．
（1）求证：∠AOB＝∠CDB；
（2）若△COD是等腰三角形，∠AOC＝140°，求∠AOB的度数．
26．如图1所示，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD，以AD为直角边，A为直角顶点，在AD左侧作等腰直角三角形ADF，连接CF，AB=AC，∠BAC=90°．
（1）当点D在线段BC上时（不与点B重合），线段CF和BD的数量关系与位置关系分别是什么？请给予证明．
（2）当点D在线段BC的延长线上时，（1）的结论是否仍然成立？请在图2中画出相应的图形，并说明理由．
参考答案
1．【考点】轴对称图形
【分析】根据轴对称图形的概念求解即可．
解：A．不是轴对称图形；
B．不是轴对称图形；
C．是轴对称图形；
D．不轴对称图形．
故选C．
【点睛】轴对称图形的判断方法：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．
2．【考点】轴对称图形
【分析】根据轴对称图形的概念求解即可．
解：A、不是轴对称图形，本选项错误；
B、不是轴对称图形，本选项错误；
C、不是轴对称图形，本选项错误；
D、是轴对称图形，本选项正确．
故选：D．
【点睛】本题考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
3．【考点】线段垂直平分线
【分析】首先连接BE，由DE是线段AB的垂直平分线，即可得BE=AE=2，即可求得答案．
解：连接BE．
∵DE是线段AB的垂直平分线，∴BE=AE．
∵AE=2，∴BE=2，即B、E两点间的距离是2．
故选A．
【点睛】本题考查了线段垂直平分线的性质．此题比较简单，注意垂直平分线上任意一点，到线段两端点的距离相等．
4．【考点】轴对称图形
【分析】A可以直接连接作对称轴，B、C需要找中点，D．还需要作水平和竖直的对称轴．
解：A．如图：； B．如图：；
C．如图：； D．如图：．
故选A．
【点睛】本题考查了轴对称图形的知识，解答本题的关键是掌握对称轴的定义．
5．【考点】轴对称图形的对称轴
【分析】轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，然后找出对称轴即可．
解：A、此图有2条对称轴，故此选项不合题意；
B、此图有4条对称轴，故此选项不合题意；
C、此图不是轴对称图形，没有对称轴，故此选项不合题意；
D、此图有3条对称轴，故此选项符合题意．
故选：D．
【点睛】本题考查了轴对称图形的对称轴，找对称轴可以采用折叠的方法，也可找到一对对应点，然后做出这对对应点所连线段的垂直平分线．
6．【考点】角平分线的性质定理，全等三角形的判定与性质
【分析】根据角平分线的性质得到PC=PD，进而根据HL证明Rt△PCO≌Rt△PDO可以判断B和D，再证明△COE≌△DOE，可以判断A和C．
解：∵OP为∠AOB的平分线，PC⊥OA，PD⊥OB，
∴PC=PD．
在Rt△PCO和Rt△PDO中，∵PC=PD，PC=PC，
∴Rt△PCO≌Rt△PDO，
∴OC=OD，故D正确；
∵OC=OD，∠COP=∠DOP，OE=OE，
∴△COE≌△DOE，
∴CE=DE，故A正确；
∵Rt△PCO≌Rt△PDO，
∴∠CPO=∠DPO，而∠CPO不一定等于∠DEP，
∴无法判断∠CPO和∠DEP的大小关系，故B错误；
∵△COE≌△DOE，∴∠CEO=∠DEO，故C正确．
故选B．
【点睛】本题考查了角平分线的性质定理以及全等三角形的判定与性质．证明Rt△PCO≌Rt△PDO是解题的关键．
7．【考点】翻折变换
【分析】根据图形翻折变换的性质得出AD=BD，故AC+（CD+AD）=AC+BC，由此即可得出结论．
解：∵△ADE由△BDE翻折而成，∴AD=BD．
∵AC=5cm，BC=10cm，∴△ACD的周长=AC+CD+AD=AC+BC=15cm．
故选C．
【点睛】本题考查了翻折变换，熟知图形翻折不变性的性质是解答此题的关键．
8．【考点】等腰三角形的性质，三角形的内角和定理
【分析】由题意可知等腰三角形的另一个底角是35°，则由三角形内角和定理即可求解其顶角.
解：由等腰三角形的性质可知其另一底角是35°，由三角形的内角和定理可知其顶角为180°-35°×2=110°，
故选择C.
【点睛】本题考查了等腰三角形的性质及三角形的内角和定理.
9．【考点】轴对称的性质，直角三角形的判定
【分析】①不存在SSA这种判定全等三角形的方法；②根据角的轴对称性进行判断；③斜边和一条直角边对应相等的两个直角三角形全等，据此判断即可；④根据轴对称的性质进行判断；⑤根据线段垂直平分线的性质进行判断．
解：①两边和其中一边的对角对应相等的两个三角形不一定全等，故①错误；
②角的对称轴是角平分线所在直线，故②错误；
③两边对应相等的两直角三角形不一定全等，故③错误；
④根据轴对称的性质可得，成轴对称的两图形一定全等，故④正确；
⑤根据中垂线的性质定理的逆定理可得，到线段两端距离相等的点在线段的垂直平分线上，故⑤正确；
综上所述，正确的说法有2个．
故选A．
【点睛】本题主要考查了轴对称的性质、直角三角形的判定、线段和角的轴对称性的综合应用，解题时注意：对称轴是一条直线；直角三角形的判定方法最多，使用时应该抓住“直角”这个隐含的已知条件．
10．【考点】线段垂直平分线的性质，等腰三角形的性质与判定
【分析】由AB的垂直平分线DE交AC于D，交AB于E，可得AD=BD，即可求得∠ABD=∠A=36°，又由AB=AC，即可求得∠CBD=∠ABD=36°，∠BDC=∠C=72°，继而证得AD=BD=BC，△BDC的周长等于AB+BC．
解：∵AB的垂直平分线DE交AC于D，交AB于E，∴AD=BD，∴∠ABD=∠A=36°，∵AB=AC，∴∠ABC=∠C=72°，∴∠CBD=∠ABD=36°，即BD平分∠ABC；故①正确；∴∠BDC=∠C=72°，∴BC=BD，∴BC=BD=AD，故②正确；∴△BDC的周长为：BC+CD+BD=BC+C+AD=AC+BC=AB+BC；故③正确；∵CD＜BD，∴CD＜AD，∴D不是AC中点．故④错误．故答案为：C
【点睛】此题考查了线段垂直平分线的性质（垂直平分线垂直且平分其所在线段）以及等腰三角形的性质与判定．此题难度不大，注意掌握数形结合思想的应用．
11．【考点】腰三角形的性质
【分析】根据等腰三角形的两底角相等，设底角的度数为x，则顶角的度数为4x，利用三角形的内角和定理即可求得x的值，进而求得顶角的度数．
解：设底角的度数为x，则顶角的度数为4x，根据题意得：
x+x+4x=180
解得：x=30．
当x=30时，顶角=4x=4×30°=120°．
故答案为：120°．
【点睛】本题考查了等腰三角形的性质：等腰三角形的两个底角相等，正确利用方程思想是关键．
12．【考点】三角形的外角性质，角平分线的性质
【分析】由AD是△ABC的角平分线求得∠BAC=40°，可得∠FAC=140°，再由外角平分线求出∠FAE=70°，利用三角形的外角等于和它不相邻的两个内角的和,得出∠B+∠E=∠FAE, 即可求得∠B的度数.
解：
∵AD是△ABC的角平分线，
∴∠BAC=2∠BAD，
∵ ∠BAD＝20°，
∴∠BAC=40°，
∵∠BAC+∠FAC=180°，
∴∠FAC=140°，
又∵AE是∠FAC的角平分线，
∴∠FAE=∠FAC=70°，
又∵∠FAE =∠B+∠E，∠E=30°，
∴∠B=70°-30°=40°.
故答案为：40°.
【点睛】本题考查三角形的外角性质，解题的关键是要熟知三角形的外角等于与它不相邻的两个内角的和.
13．【考点】轴对称图形的概念
【分析】根据轴对称图形的概念确定出对称轴的条数，然后判断即可．
解：①有4条对称轴，②有6条对称轴，③有4条对称轴，④有2条对称轴．
所以，对称轴的条数大于3的有3个．
故答案为：3．
【点睛】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
14．【考点】邻补角与折叠的性质
【分析】先用邻补角求出∠DEF，再根据折叠的性质即可求出∠AED.
解：∵∠CEF=60°，
∴∠DEF=120°，
∵折叠，
∴∠AED=∠DEF=60°.
【点睛】此题主要考查邻补角与折叠的性质，解题的关键是熟知邻补角的特点.
15．【考点】角平分线性质
【分析】过D作DE⊥AB于E，则DE=6，根据角平分线性质求出CD=DE=6，求出BD即可．
解：过D作DE⊥AB于E．
∵点D到边AB的距离为6，∴DE=6．
∵∠C=90°，AD平分∠BAC，DE⊥AB，∴CD=DE=6．
∵CDDB，∴DB=12，∴BC=6+12=18．
故答案为：18．
【点睛】本题考查了角平分线性质的应用，注意：角平分线上的点到这个角的两边的距离相等．
16．【考点】三角形的内角和，等腰三角形的性质
解：∵AB=BC=CD=DE=EF，∠A=15°，
∴∠BCA=∠A=15°，
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°，
∴∠BCD=180°-（∠CBD+∠BDC）=180°-60°=120°，
∴∠ECD=∠CED=180°-∠BCD-∠BCA=180°-120°-15°=45°，
∴∠CDE=180°-（∠ECD+∠CED）=180°-90°=90°，
∴∠EDF=∠EFD=180°-∠CDE-∠BDC=180°-90°-30°=60°，
∴∠DEF=180°-（∠EDF+∠EFD）=180°-120°=60°．
【点睛】三角形的内角和是180度．求角的度数常常要用到“三角形的内角和是180°这一隐含的条件．
17．【考点】轴对称的性质
【分析】根据轴对称的性质，结合网格结构，分横向、纵向和斜向三种情况确定出不同的对称轴的位置，然后作出与△ABC成轴对称的格点三角形，从而得解．
解：如图所示，对称轴有三种位置，与△ABC成轴对称的格点三角形有3个．
故答案为：3．
【点睛】本题考查了轴对称的性质，难点在于确定出对称轴的不同位置．
18．【考点】线段垂直平分线的性质、三角形全等的判定
【分析】根据题意AB=AD，BC=DC，AC与BD相交于点O可以证明△ABC≌△ADC、△ABO≌△ADO，可得AC、BD互相垂直，AC平分∠BAD、∠BCD．
解：∵在△ABC与△ADC中，，
∴△ABC≌△ADC（SSS），
∴∠BAO=∠DAO，∠BCO=∠DCO，即AC平分∠BCD．故③正确；
∵AC平分∠BAD、∠BCD，△ABD与△BCD均为等腰三角形，∴AC、BD互相垂直，但不平分．故①正确，②错误；
由题中条件无法证明∠ABC=∠ADC=90°，故④错误；
∵AC、BD互相垂直，∴筝形ABCD的面积为：AC?BOAC?ODAC?BD．
故⑤正确；
综上所述：正确的说法是①③⑤．
故答案为：①③⑤．
【点睛】本题考查了线段垂直平分线的性质、三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．再运用全等三角形的性质可得相应的结论．
19．【考点】作图﹣轴对称变换
【分析】根据轴对称图形的特点：沿一条直线对折后，直线两旁的部分能完全重合画图即可．
解：如图所示：
．
【点睛】本题考查了作图﹣轴对称变换，其依据是轴对称的性质．
基本作法：①先确定图形的关键点；
②利用轴对称性质作出关键点的对称点；
③按原图形中的方式顺次连接对称点．
20．【考点】等腰三角形的性质
【分析】由平行线的性质可得∠D=∠DBC，∠DAC=∠ACB，再由等腰三角形的性质可得∠ABC的度数，等量代换即可得到结论．
解：∵AD∥BC，
∴∠D=∠DBC，∠DAC=∠ACB．
∵AB=AC=AD，
∴∠D=∠ABD，∠ACB=∠ABC=∠ABD＋∠DBC=2∠D=2×35°=70°．
∴∠DAC=70°．
【点睛】本题考查了等腰三角形的性质，掌握等腰三角形的两底角相等是解题的关键．
21．【考点】等腰三角形的性质
【分析】根据三线合一定理证明CE平分∠ACD，然后根据CF平分∠ACB，根据邻补角的定义即可证得．
解：CE⊥CF．理由如下：
∵CD=CA，E是AD的中点，∴∠ACE=∠DCE．
∵CF平分∠ACB，∴∠ACF=∠BCF．
∵∠ACE+∠DCE+∠ACF+∠BCF=180°，∴∠ACE+∠ACF=90°．
即∠ECF=90°，∴CE⊥CF．
【点睛】本题考查了等腰三角形的性质，顶角的平分线、底边上的中线和高线、三线合一．
22．【考点】等腰三角形的判定与性质，线段垂直平分线的性质
【分析】先根据线段垂直平分线及等腰三角形的性质得出∠B=∠DAB，再根据∠DAE与∠DAC的度数比为2：1，可设出∠DAC的度数，由直角三角形的性质列出方程，求出∠B的度数即可．
解：∵D是线段AB垂直平分线上的点，
∴AD=BD，
∴△DAB是等腰三角形，∠B=∠DAB．
∵∠DAE与∠DAC的度数比为2：1，
∴设∠DAC=x，则∠B=∠DAB=2x，
∴x+2x+2x=90°，
∴x=18°，即∠B=36°．
【点睛】本题考查了等腰三角形的判定与性质以及线段垂直平分线的性质，属较简单题目．
23．【考点】作图﹣应用与设计作图，角平分线的性质，线段垂直平分线的性质
【分析】分别作线段CD的垂直平分线和∠AOB的角平分线，它们的交点即为点P．
解：如图，到∠AOB两边距离相等的点在这个角的平分线上，而到宣传牌C，D的距离相等的点则在线段CD的垂直平分线上，故它们的交点P即为所求．
【点睛】本题考查了作图﹣应用与设计作图，熟知角平分线的性质与线段垂直平分线的性质是解答此题的关键．
24．【考点】轴对称的性质，三角形面积求法
【分析】利用AC⊥BD于点E，BE=DE，得出S阴影=S△ABC，进而得出答案即可．
解：∵AC⊥BD，BE＝DE，
∴点B，D关于直线AC对称，
又∵点E在AC上，
∴△BEF与△DEF关于直线AC对称，
∴△BEF≌△DEF，
∴S阴影＝S△ABC，
又∵BD＝8，
∴BE＝4，
∴S△ABC＝AC·BE＝×10×4＝20(cm2)
【点睛】此题考查了轴对称的性质以及三角形面积求法，利用轴对称图形的性质得出S阴影=S△ABC是解题关键．
25．【考点】等腰直角三角形的性质，全等三角形的判定和性质
【分析】（1）根据等腰直角三角形的性质和全等三角形的判定和性质解答即可；
（2）设∠AOB的度数为x，分三种情况进行解答即可．
解：（1）∵△ABC和△OBD是等腰直角三角形，
∴AB＝BC，OB＝BD，∠ABC＝∠OBD＝90°，
∵∠ABO+∠OBC＝∠CBD+∠OBC，
∴∠ABO＝∠CBD，
在△ABO和△CBD中
，
∴△ABO≌△CBD（SAS），
∴∠AOB＝∠CDB；
（2）设∠AOB的度数为x，则∠CDB＝x，∠CDO＝x﹣45°，
∠COD＝∠COB﹣∠DOB＝360°﹣140°﹣x﹣45°＝175°﹣x，
∠OCD＝180°﹣∠CDO﹣∠COD＝50°，
①当∠CDO＝∠COD时，x﹣45°＝175°﹣x，解得：x＝110°，
②当∠CDO＝∠OCD时，x﹣45°＝50°，解得：x＝95°，
③当∠COD＝∠OCD时，175°﹣x＝50°，解得：x＝125°，
故∠AOB的度数为110°或95°或125°．
【点睛】本题考查了全等三角形的判定与性质，关键是根据等腰直角三角形的性质和全等三角形的判定和性质解答．
26．【考点】全等三角形的判定与性质，等腰直角三角形的性质
【分析】（1）根据同角的余角相等求出∠CAF=∠BAD，然后利用“边角边”证明△ACF和△ABD全等，根据全等三角形对应边相等可得CF=BD，全等三角形对应角相等可得∠ACF=∠B，然后求出∠BCF=90°，从而得到CF⊥BD；
（2）先求出∠CAF=∠BAD，然后与①的思路相同求解即可；
解：（1）CF=BD，且CF⊥BD，证明如下：
∵∠FAD=∠CAB=90°，
∴∠FAC=∠DAB．
在△ACF和△ABD中，
，
∴△ACF≌△ABD
∴CF=BD，∠FCA=∠DBA，
∴∠FCD=∠FCA+∠ACD=∠DBA+∠ACD=90°，
∴FC⊥CB，
故CF=BD，且CF⊥BD．
（2）（1）的结论仍然成立，如图2，
∵∠CAB=∠DAF=90°，
∴∠CAB+∠CAD=∠DAF+∠CAD，
即∠CAF=∠BAD，
在△ACF和△ABD中，
，
∴△ACF≌△ABD，
∴CF=BD，∠ACF=∠B，
∵AB=AC，∠BAC=90°，
∴∠B=∠ACB=45°，
∴∠BCF=∠ACF+∠ACB=45°+45°=90°，
∴CF⊥BD；
∴CF=BD，且CF⊥BD．
【点睛】本题考查了全等三角形的判定与性质，等腰直角三角形的性质，根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键，此类题目的特点是各小题求解思路一般都相同．