人教版七年级下册5.3.1平行线的性质课件 (21张PPT)
文档属性
| 名称 | 人教版七年级下册5.3.1平行线的性质课件 (21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-16 16:40:38 | ||
图片预览

文档简介
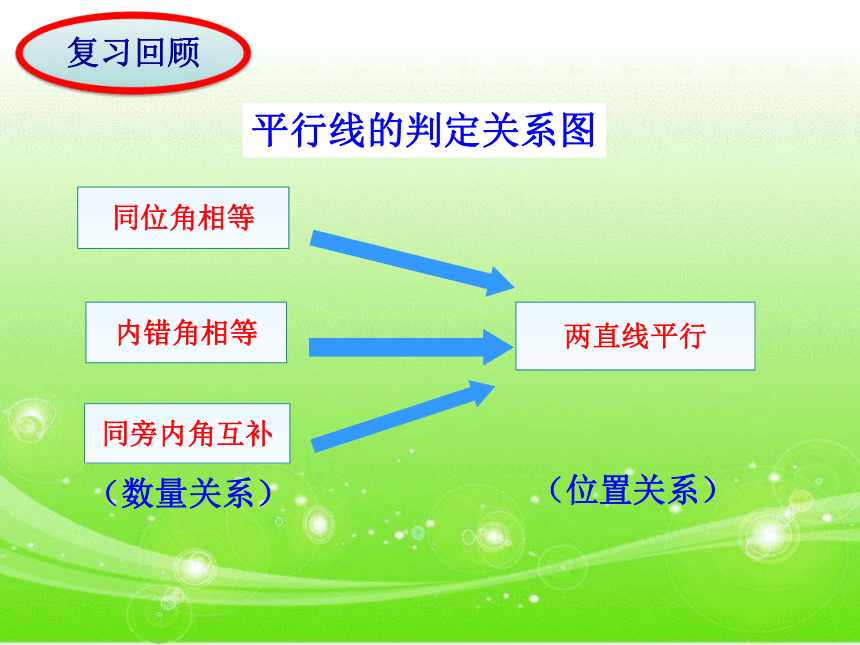
课件21张PPT。 《5.3.1平行线的性质》 人教版七年级下册数学同位角相等内错角相等同旁内角互补两直线平行
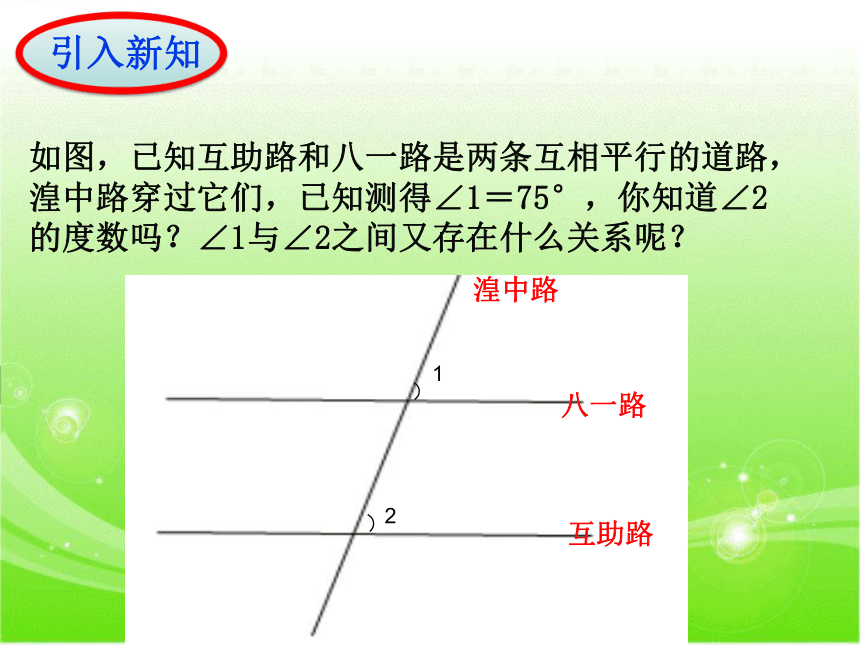
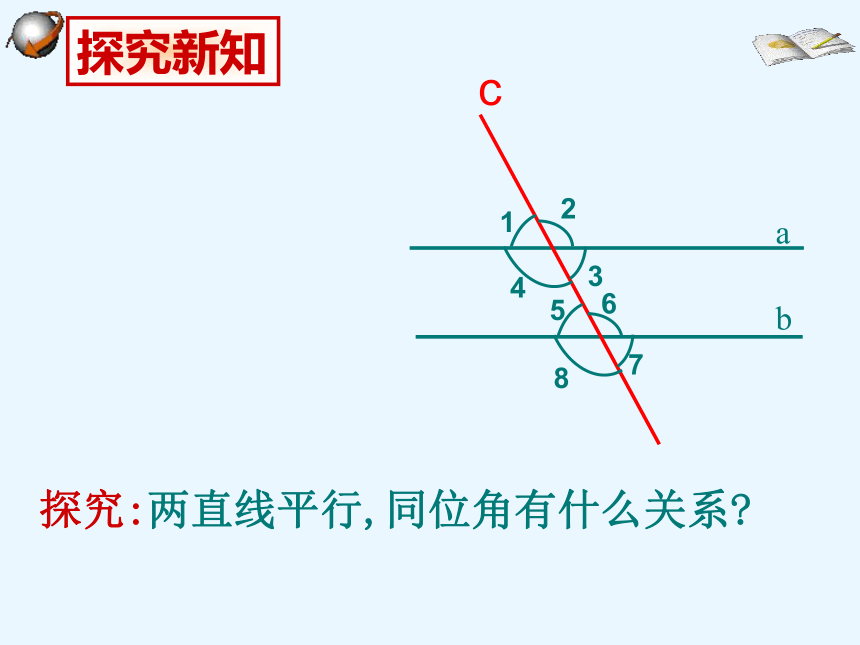
(数量关系)(位置关系)平行线的判定关系图复习回顾引入新知如图,已知互助路和八一路是两条互相平行的道路,湟中路穿过它们,已知测得∠1=75°,你知道∠2的度数吗?∠1与∠2之间又存在什么关系呢?互助路八一路湟中路))12探究:两直线平行,同位角有什么关系?ab如图,直线a∥b,
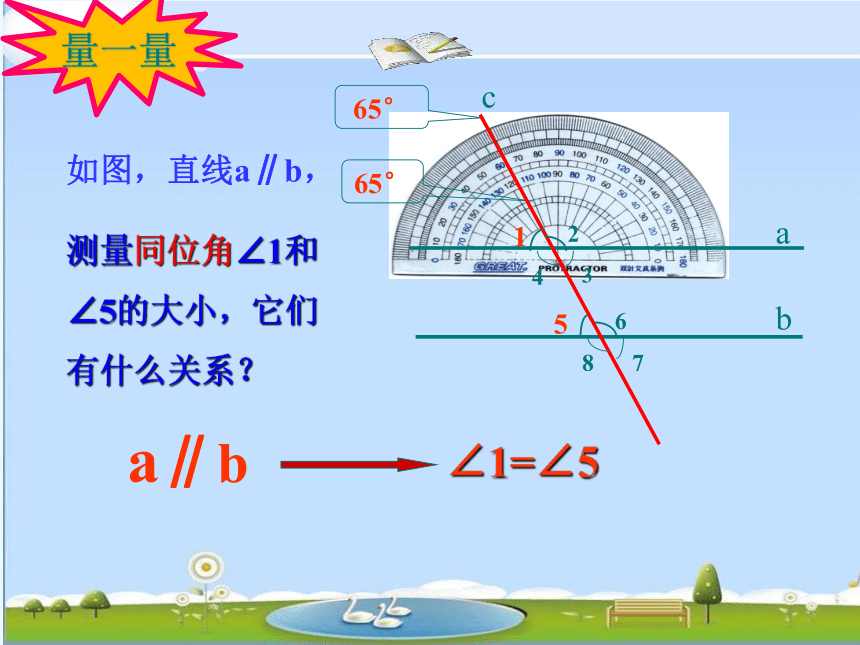
测量同位角∠1和∠5的大小,它们有什么关系?
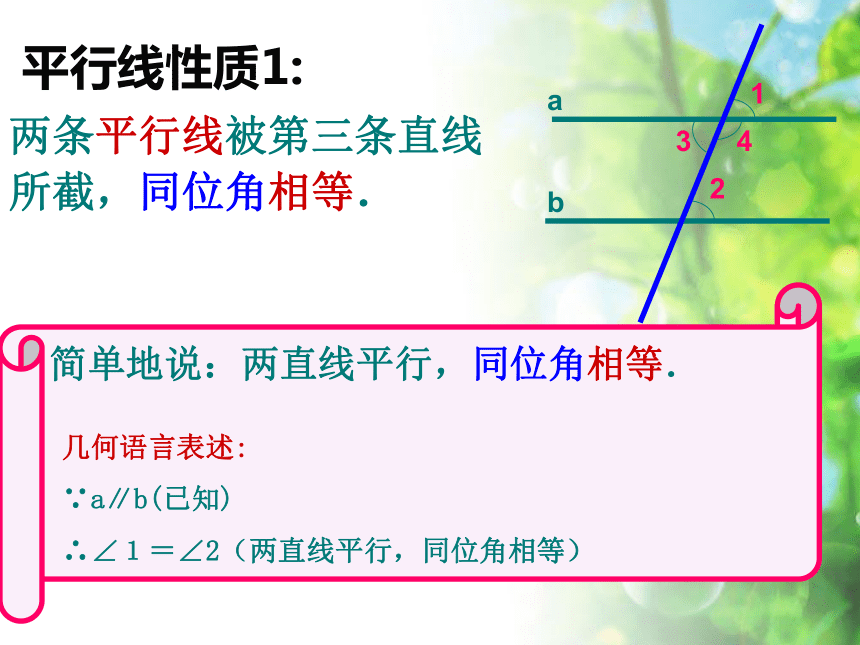
65°65°cab15243687∠1=∠5a∥b量一量两条平行线被第三条直线所截,同位角相等.平行线性质1:
几何语言表述:
∵a∥b(已知)
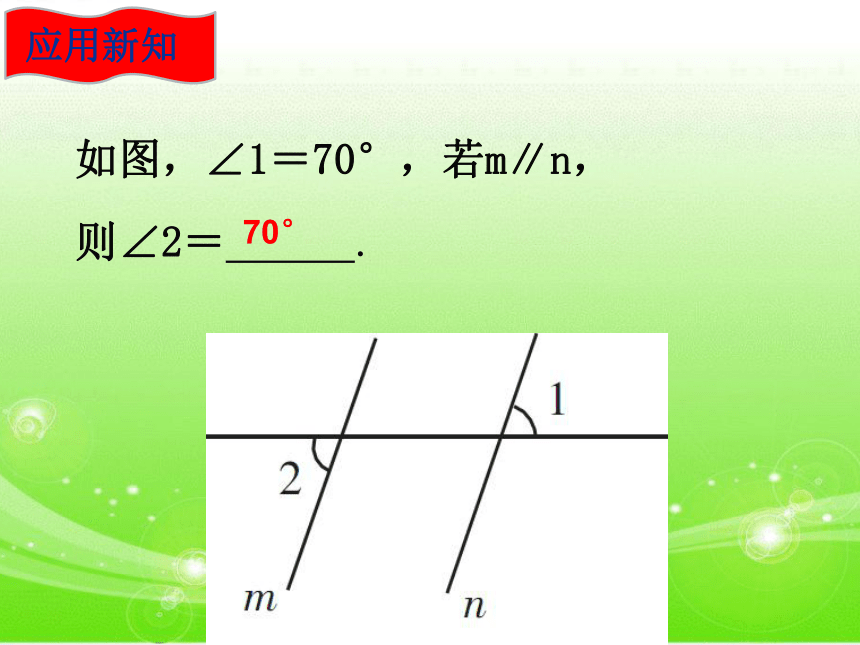
∴∠1=∠2(两直线平行,同位角相等)简单地说:两直线平行,同位角相等.如图,∠1=70°,若m∥n,
则∠2= .
70°应用新知 3解: a//b (已知)
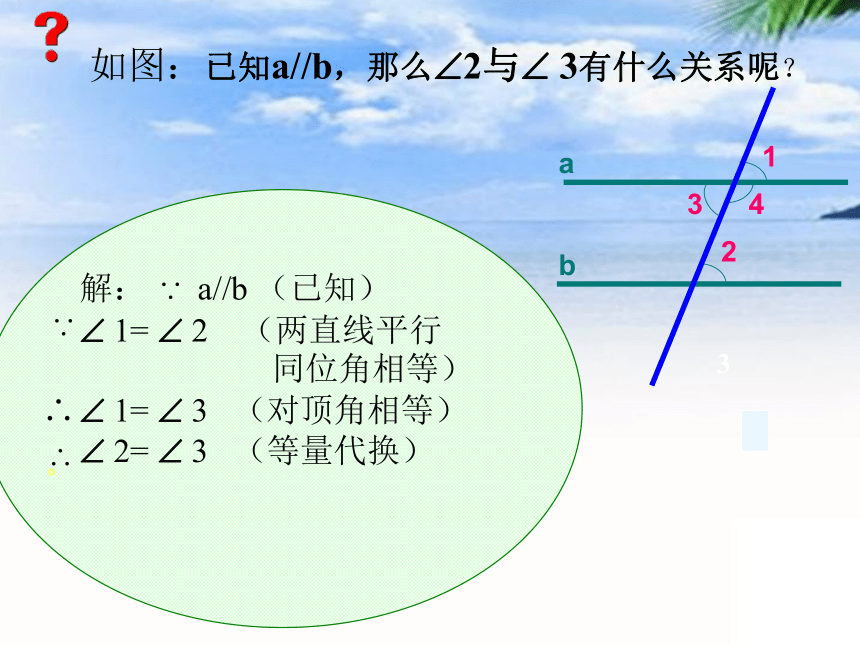
? 1= ? 2 (两直线平行
同位角相等)
? 1= ? 3 (对顶角相等)
? 2= ? 3 (等量代换)
如图:已知a//b,那么?2与? 3有什么关系呢?。
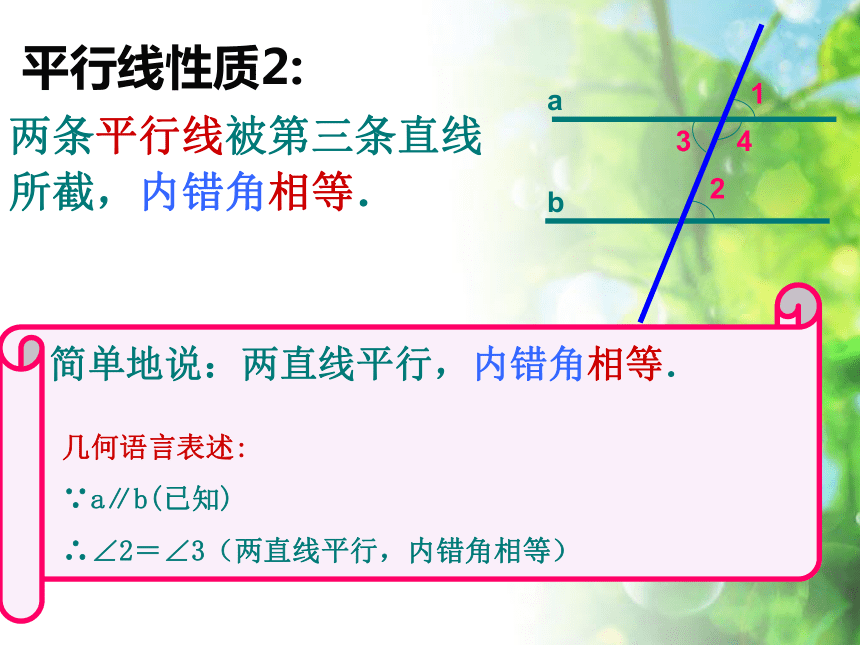
????两条平行线被第三条直线所截,内错角相等.平行线性质2:
几何语言表述:
∵a∥b(已知)
∴∠2=∠3(两直线平行,内错角相等)简单地说:两直线平行,内错角相等.
如图,直线AB∥CD,直线 分别与AB,CD相交,若∠1=50°,则∠2的度数为 .
应用新知BD50° 3解: a//b (已知)
? 1= ? 2 (两直线平行
同位角相等)
? 1+ ? 4=180°(邻补角定义)
? 2+ ? 4=180°(等量代换)
如图:已知a//b,那么?2与? 4有什么关系呢?。
???。
两条平行线被第三条直线所截,同旁内角互补.平行线性质3:
几何语言表述:
∵a∥b(已知)
∴∠2+∠4= (两直线平行,同旁内角互补)简单地说:两直线平行,同旁内角互补.如图,若m∥n,∠1=105°,则∠2= .
应用新知75°类比“直线平行的判定”与“平行线的性质”判定 性质1、同位角相等,
两直线平行1、两直线平行,
同位角相等2、内错角相等,
两直线平行2、两直线平行,
内错角相等3、同旁内角互补,
两直线平行3、两直线平行,
同旁内角互补类比记忆平行线的“判定”与“性质”
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度?为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
2∠4=70o
∵两直线平行,同旁内角互补巩固新知如图,AC∥BD,∠A=70°,∠C=50°,则∠1= ,∠2= , ∠3= .70°50°60°巩固新知
如图,直线a∥b, ∠1=54o,
那么∠2、∠3、∠4各是多少度?1234∠2 = ∠1=54o( ),
∠4 = ∠1=54o( ),
∠3=180°-∠4 =180°-54°=126°( ) 对顶角相等两直线平行,同位角相等邻补角的定义巩固练习两直线平行判定性质(1)请你总结一下本节课所学的内容。小结与回顾:(2)说说平行线的“判定”与“性质”有什么不同?
同位角相等
内错角相等
同旁内角互补类比直线平行的
条件平行线的
性质由角的大小关系转化为直线的位置关系由直线的位置关系转化为角的大小关系布置作业西宁市第二十八中学
2019年3月18日谢谢
(数量关系)(位置关系)平行线的判定关系图复习回顾引入新知如图,已知互助路和八一路是两条互相平行的道路,湟中路穿过它们,已知测得∠1=75°,你知道∠2的度数吗?∠1与∠2之间又存在什么关系呢?互助路八一路湟中路))12探究:两直线平行,同位角有什么关系?ab如图,直线a∥b,
测量同位角∠1和∠5的大小,它们有什么关系?
65°65°cab15243687∠1=∠5a∥b量一量两条平行线被第三条直线所截,同位角相等.平行线性质1:
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)简单地说:两直线平行,同位角相等.如图,∠1=70°,若m∥n,
则∠2= .
70°应用新知 3解: a//b (已知)
? 1= ? 2 (两直线平行
同位角相等)
? 1= ? 3 (对顶角相等)
? 2= ? 3 (等量代换)
如图:已知a//b,那么?2与? 3有什么关系呢?。
????两条平行线被第三条直线所截,内错角相等.平行线性质2:
几何语言表述:
∵a∥b(已知)
∴∠2=∠3(两直线平行,内错角相等)简单地说:两直线平行,内错角相等.
如图,直线AB∥CD,直线 分别与AB,CD相交,若∠1=50°,则∠2的度数为 .
应用新知BD50° 3解: a//b (已知)
? 1= ? 2 (两直线平行
同位角相等)
? 1+ ? 4=180°(邻补角定义)
? 2+ ? 4=180°(等量代换)
如图:已知a//b,那么?2与? 4有什么关系呢?。
???。
两条平行线被第三条直线所截,同旁内角互补.平行线性质3:
几何语言表述:
∵a∥b(已知)
∴∠2+∠4= (两直线平行,同旁内角互补)简单地说:两直线平行,同旁内角互补.如图,若m∥n,∠1=105°,则∠2= .
应用新知75°类比“直线平行的判定”与“平行线的性质”判定 性质1、同位角相等,
两直线平行1、两直线平行,
同位角相等2、内错角相等,
两直线平行2、两直线平行,
内错角相等3、同旁内角互补,
两直线平行3、两直线平行,
同旁内角互补类比记忆平行线的“判定”与“性质”
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度?为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
2∠4=70o
∵两直线平行,同旁内角互补巩固新知如图,AC∥BD,∠A=70°,∠C=50°,则∠1= ,∠2= , ∠3= .70°50°60°巩固新知
如图,直线a∥b, ∠1=54o,
那么∠2、∠3、∠4各是多少度?1234∠2 = ∠1=54o( ),
∠4 = ∠1=54o( ),
∠3=180°-∠4 =180°-54°=126°( ) 对顶角相等两直线平行,同位角相等邻补角的定义巩固练习两直线平行判定性质(1)请你总结一下本节课所学的内容。小结与回顾:(2)说说平行线的“判定”与“性质”有什么不同?
同位角相等
内错角相等
同旁内角互补类比直线平行的
条件平行线的
性质由角的大小关系转化为直线的位置关系由直线的位置关系转化为角的大小关系布置作业西宁市第二十八中学
2019年3月18日谢谢
