人教版七年级数学下册8.1 二元一次方程组(共33张PPT)
文档属性
| 名称 | 人教版七年级数学下册8.1 二元一次方程组(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-16 10:35:53 | ||
图片预览











文档简介
课件33张PPT。1激情引入 某队在10场比赛中得到16分,那么这个队胜负场数分别是多少? 篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.2激趣导入 在上面的问题中,要求的是两个未知数.如果用一元一次方程来解决,列方程时,要用一个未知数表示另一个未知数。
能不能根据题意直接设两个未知数,使列方程变得容易呢?我们从这个想法出发开始本章的学习.如:设胜场数为x,则负场数为(10-x),根据题意得,2x+(10-x)=163人教版七年级数学下册第八章 二元一次方程组8.1 二元一次方程组 1.知道二元一一次方程、二元一次方程组的概念
及其解的意义.
2.会判断两个未知数的值是否为二元一-次方程
(组)的解.
3.初步认识二元一-次方程(组)在解决实际问题
中的作用.重点:二元一次方程(组)的概念,二元一次方程
(组)的解.
难点:二元一次方程(组)的解及特殊解.4学习目标重点难点5知识链接诗歌中的方程
明代程大位有一首数学饮酒诗这样写道:“肆中饮客乱纷纷,薄酒名醨厚酒醇.好酒一瓶醉三客,薄酒三瓶醉一人.共同饮了一十九,三十三客醉颜生.试问高明能算士,几多醨酒几多醇?”这首诗题大意是说好酒一瓶,可以醉倒3位客人,薄酒三瓶,可以醉倒一位客人.如果33位客人醉倒了,他们总共饮下19瓶酒.试向:其中好酒、薄酒分别是多少瓶?
你看,在我国古代,不但诗词歌赋令我们陶醉,其中所蕴含的数学知识也值得我们回味!好酒10瓶,薄酒9瓶6复习备用1.下列方程是一元一次方程的是 . (填序号)
① x+y=7;② 3x -9=x+6;③ 1/x-5=x;④ x+x2=1
2.下列各数:① x= 1;② x= -1;③ x=0;④ x=-7, 是方程2x+3=x-4 的解.
3.知识回顾:含有 个未知数,且含有未知数的项的次数都是 次的方程叫做一元一次方程;能够使方程左右两边
的未知数的值叫做方程的解.②相等一一④ 除了两个显性条件“一个未知数、一次"之外,还有一个隐性条件----"整式方程”.7 篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?能不能设两个未知数来解决问题?设胜x场,负y场根据题意很容易得方程:
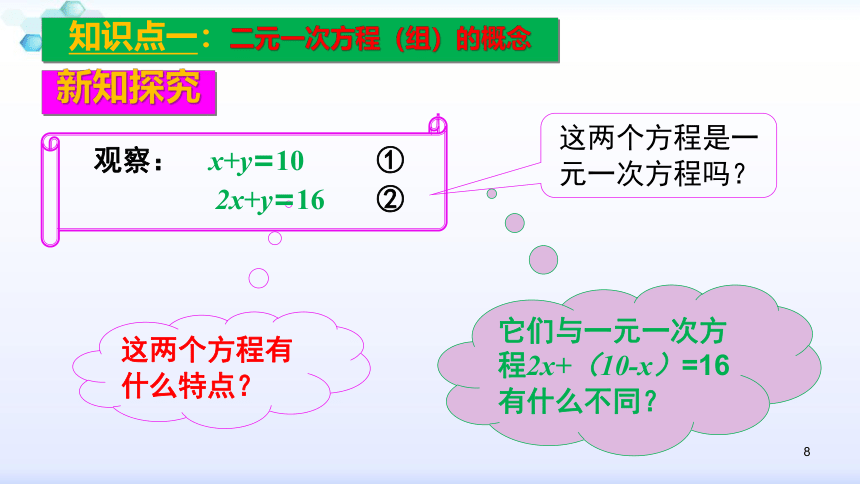
x+y=10
2x+y=16新知探究知识点一:二元一次方程(组)的概念8新知探究知识点一:二元一次方程(组)的概念这两个方程是一元一次方程吗? 这两个方程有什么特点? 它们与一元一次方程2x+(10-x)=16有什么不同? 观察: x+y=10 ①
2x+y=16 ② 9新知探究知识点一:二元一次方程(组)的概念 含有两个未知数(x和 y),并且未知数的次数都是1,这样的方程叫做二元一次方程. 10学以致用知识点一:二元一次方程(组)的概念1、判断下列式子哪些是二元一次方程?(1) 3x+5y=z(5) x+y=12y(2) x2+y=0√(7) xy+y=12√(8) x+y=y11归纳小结知识点一:二元一次方程(组)的概念 判断一个方程是否为二元一次方程的方法:
一看原方程是否是整式方程且只含有两个未知数;
二看整理化简后的方程是否具备两个未知数的系数都不为0,且含未知数的项的次数都是1.12新知探究知识点一:二元一次方程(组)的概念 上面的问题中包含了两个必须同时满足的条件,也就是未知数x,y必须同时满足方程 x+y=10 和2x+y=16.
把两个方程合在一起,写成
这个方程组含有几个未知数?
含有未知数的项的次数是多少?就组成了一个方程组.13新知探究知识点一:二元一次方程(组)的概念 含有两个未知数,每个未知数的项的次数都是1,并且一共有两个方程,像这样的方程组叫做二元一次方程组. 14学以致用知识点一:二元一次方程(组)的概念2.判断下列各方程组是不是二元一次方程组,试说明理由。15归纳小结知识点一:二元一次方程(组)的概念2.含未知数的项的次数是1 (整式方程)3.两个方程 判断一个方程组是否为二元一次方程组的方法:
1.含两个未知数;“一次”是指含未知数的项的次数是1,而不是未知数的次数 先独立完成导学案互动探究1-2,再同桌相互交流,
最后小组交流;16合作探究知识点一:二元一次方程(组)的概念17新知探究知识点二:二元一次方程(组)的解的概念满足方程①且符合实际意义的x,y的值有哪些?把它们填入表中: 012345689107109876543210 由上表可知,x=0, y=10; x=1, y=9; ...; x=10, y=0使方程x+y=10两边的值相等,它们都是方程x+y= 10的解.如果不考虑方程x+y= 10与上面实际问题的联系,那么x=-1, y=11; x=0.5, y=9.5;
....都是这个方程的解. 一般地,一个二元一次方程有无数个解18新知探究知识点二:二元一次方程(组)的解的概念 一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。19新知探究知识点二:二元一次方程(组)的解的概念 二元一次方程的解和一元一次方程的解有什么区别?一个无数个一个未知数的值一对未知数的值结论:二元一次方程有无数个解。20新知探究知识点二:二元一次方程(组)的解的概念刚才表格中的x,y的值有没有满足方程②的?
21新知探究知识点二:二元一次方程(组)的解的概念 x=6,x=4既满足方程①。又满足方程②.也就是说, x=6,x=4 是方程①与方程②的公共解,我们把x=6,x=4叫做二元
一次方程组 的解.常记作 一般地,二元一次方程组的两个方程的公共解,叫做这个二元一次方程组的解。联系前面的实际问题可知,这个队在10场比赛中胜6场、负4场.22学以致用知识点二:二元一次方程(组)的解的概念C1.下列不是二元一次方程组的是( )A.B.B23学以致用知识点二:二元一次方程(组)的解的概念(1) 是方程①x-3y=2解;(2) 是方程②2x-y=9解;ABBDB3.下列各组数中,24典例讲评知识点二:二元一次方程(组)的解的概念例1、若3xm+1+5y2-n=3,是一个二元一次方程,
则m= ,n= .01解析:根据题意得:解得:25新知探究知识点二:二元一次方程(组)的解的概念例2. 若 是方程组 的解,
则m=_____ , n=______ 30.5先独立完成导学案互动探究3、4,再同桌相互交
流,最后小组交流;26合作探究知识点二:二元一次方程(组)的解的概念27新知探究知识点二:二元一次方程(组)的解的概念C128新知探究知识点二:二元一次方程(组)的解的概念3.若 是关于x,y的二元一次方程组 的解,则a-b= .
4.方程2x+y=5的正整数解是 . 129归纳总结只含有一个未知数,且未知数的项的次数是1的方程含有两个未知数,且未知数的项的次数都是1的方程使一元一次方程两边的值相等的未知数的值,使二元一次方程两边的值相等的两个未知数的值代入,使方程两边值相等就是解含有两个未知数,并且未知数的项的次数都是1,共有2个方程的方程组二元一次方程组的2个方程的公共解代入,使方程两边值相等就是解代入,使两个方程两边值都相等就是解30思维导图二元一次方程组二元一次方程二元一次方程组二元一次方程的解二元一次方程组的解知识结构图31x 轴y 轴原点+,+-,+-,-+,-y=0 x=0 x=y x=﹣y 加减加减32 对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?蓦然回首331.课本第89页练习:习题8.1第1-5题;
2.《导学测评》第24页;作业布置
能不能根据题意直接设两个未知数,使列方程变得容易呢?我们从这个想法出发开始本章的学习.如:设胜场数为x,则负场数为(10-x),根据题意得,2x+(10-x)=163人教版七年级数学下册第八章 二元一次方程组8.1 二元一次方程组 1.知道二元一一次方程、二元一次方程组的概念
及其解的意义.
2.会判断两个未知数的值是否为二元一-次方程
(组)的解.
3.初步认识二元一-次方程(组)在解决实际问题
中的作用.重点:二元一次方程(组)的概念,二元一次方程
(组)的解.
难点:二元一次方程(组)的解及特殊解.4学习目标重点难点5知识链接诗歌中的方程
明代程大位有一首数学饮酒诗这样写道:“肆中饮客乱纷纷,薄酒名醨厚酒醇.好酒一瓶醉三客,薄酒三瓶醉一人.共同饮了一十九,三十三客醉颜生.试问高明能算士,几多醨酒几多醇?”这首诗题大意是说好酒一瓶,可以醉倒3位客人,薄酒三瓶,可以醉倒一位客人.如果33位客人醉倒了,他们总共饮下19瓶酒.试向:其中好酒、薄酒分别是多少瓶?
你看,在我国古代,不但诗词歌赋令我们陶醉,其中所蕴含的数学知识也值得我们回味!好酒10瓶,薄酒9瓶6复习备用1.下列方程是一元一次方程的是 . (填序号)
① x+y=7;② 3x -9=x+6;③ 1/x-5=x;④ x+x2=1
2.下列各数:① x= 1;② x= -1;③ x=0;④ x=-7, 是方程2x+3=x-4 的解.
3.知识回顾:含有 个未知数,且含有未知数的项的次数都是 次的方程叫做一元一次方程;能够使方程左右两边
的未知数的值叫做方程的解.②相等一一④ 除了两个显性条件“一个未知数、一次"之外,还有一个隐性条件----"整式方程”.7 篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?能不能设两个未知数来解决问题?设胜x场,负y场根据题意很容易得方程:
x+y=10
2x+y=16新知探究知识点一:二元一次方程(组)的概念8新知探究知识点一:二元一次方程(组)的概念这两个方程是一元一次方程吗? 这两个方程有什么特点? 它们与一元一次方程2x+(10-x)=16有什么不同? 观察: x+y=10 ①
2x+y=16 ② 9新知探究知识点一:二元一次方程(组)的概念 含有两个未知数(x和 y),并且未知数的次数都是1,这样的方程叫做二元一次方程. 10学以致用知识点一:二元一次方程(组)的概念1、判断下列式子哪些是二元一次方程?(1) 3x+5y=z(5) x+y=12y(2) x2+y=0√(7) xy+y=12√(8) x+y=y11归纳小结知识点一:二元一次方程(组)的概念 判断一个方程是否为二元一次方程的方法:
一看原方程是否是整式方程且只含有两个未知数;
二看整理化简后的方程是否具备两个未知数的系数都不为0,且含未知数的项的次数都是1.12新知探究知识点一:二元一次方程(组)的概念 上面的问题中包含了两个必须同时满足的条件,也就是未知数x,y必须同时满足方程 x+y=10 和2x+y=16.
把两个方程合在一起,写成
这个方程组含有几个未知数?
含有未知数的项的次数是多少?就组成了一个方程组.13新知探究知识点一:二元一次方程(组)的概念 含有两个未知数,每个未知数的项的次数都是1,并且一共有两个方程,像这样的方程组叫做二元一次方程组. 14学以致用知识点一:二元一次方程(组)的概念2.判断下列各方程组是不是二元一次方程组,试说明理由。15归纳小结知识点一:二元一次方程(组)的概念2.含未知数的项的次数是1 (整式方程)3.两个方程 判断一个方程组是否为二元一次方程组的方法:
1.含两个未知数;“一次”是指含未知数的项的次数是1,而不是未知数的次数 先独立完成导学案互动探究1-2,再同桌相互交流,
最后小组交流;16合作探究知识点一:二元一次方程(组)的概念17新知探究知识点二:二元一次方程(组)的解的概念满足方程①且符合实际意义的x,y的值有哪些?把它们填入表中: 012345689107109876543210 由上表可知,x=0, y=10; x=1, y=9; ...; x=10, y=0使方程x+y=10两边的值相等,它们都是方程x+y= 10的解.如果不考虑方程x+y= 10与上面实际问题的联系,那么x=-1, y=11; x=0.5, y=9.5;
....都是这个方程的解. 一般地,一个二元一次方程有无数个解18新知探究知识点二:二元一次方程(组)的解的概念 一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。19新知探究知识点二:二元一次方程(组)的解的概念 二元一次方程的解和一元一次方程的解有什么区别?一个无数个一个未知数的值一对未知数的值结论:二元一次方程有无数个解。20新知探究知识点二:二元一次方程(组)的解的概念刚才表格中的x,y的值有没有满足方程②的?
21新知探究知识点二:二元一次方程(组)的解的概念 x=6,x=4既满足方程①。又满足方程②.也就是说, x=6,x=4 是方程①与方程②的公共解,我们把x=6,x=4叫做二元
一次方程组 的解.常记作 一般地,二元一次方程组的两个方程的公共解,叫做这个二元一次方程组的解。联系前面的实际问题可知,这个队在10场比赛中胜6场、负4场.22学以致用知识点二:二元一次方程(组)的解的概念C1.下列不是二元一次方程组的是( )A.B.B23学以致用知识点二:二元一次方程(组)的解的概念(1) 是方程①x-3y=2解;(2) 是方程②2x-y=9解;ABBDB3.下列各组数中,24典例讲评知识点二:二元一次方程(组)的解的概念例1、若3xm+1+5y2-n=3,是一个二元一次方程,
则m= ,n= .01解析:根据题意得:解得:25新知探究知识点二:二元一次方程(组)的解的概念例2. 若 是方程组 的解,
则m=_____ , n=______ 30.5先独立完成导学案互动探究3、4,再同桌相互交
流,最后小组交流;26合作探究知识点二:二元一次方程(组)的解的概念27新知探究知识点二:二元一次方程(组)的解的概念C128新知探究知识点二:二元一次方程(组)的解的概念3.若 是关于x,y的二元一次方程组 的解,则a-b= .
4.方程2x+y=5的正整数解是 . 129归纳总结只含有一个未知数,且未知数的项的次数是1的方程含有两个未知数,且未知数的项的次数都是1的方程使一元一次方程两边的值相等的未知数的值,使二元一次方程两边的值相等的两个未知数的值代入,使方程两边值相等就是解含有两个未知数,并且未知数的项的次数都是1,共有2个方程的方程组二元一次方程组的2个方程的公共解代入,使方程两边值相等就是解代入,使两个方程两边值都相等就是解30思维导图二元一次方程组二元一次方程二元一次方程组二元一次方程的解二元一次方程组的解知识结构图31x 轴y 轴原点+,+-,+-,-+,-y=0 x=0 x=y x=﹣y 加减加减32 对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?蓦然回首331.课本第89页练习:习题8.1第1-5题;
2.《导学测评》第24页;作业布置
