青岛版八年级下册 6.4 三角形的中位线定理课件(24张PPT)
文档属性
| 名称 | 青岛版八年级下册 6.4 三角形的中位线定理课件(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-20 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
*
Page
6.4三角形的中位线定理
*
Page
聚焦质疑问题
小组合作交流:
1、从导学案中选出的5个问题和老师提的1个问题。
2、交流第6个问题时借助手中的三角形纸片。
【数学之问】
具体问题
1、 三角形的中线与中位线的区别?【崔胜壮】【王欣】【邵璐】【苏迪】【李华艺】
2、三角形有几条中位线?【马怡炜】【曹明晧】【陈伯阳】
3、三角形的三条中位线组成的三角形与原三角形的周长有什么关系?【刘亚宁】【王欣】
4、一个三角形的三条中位线分成的四个小三角形是否全等?【张继祖】
5、顺次连接任意四边形中点,得到一个怎样的图形?【何如心】【祝嘉威】
6、 怎样将一张三角形硬纸片剪成两部分,使分成的两部分能拼成一个平行四边形 【师】
A
B
C
D
E
*
Page
【数学之探究】
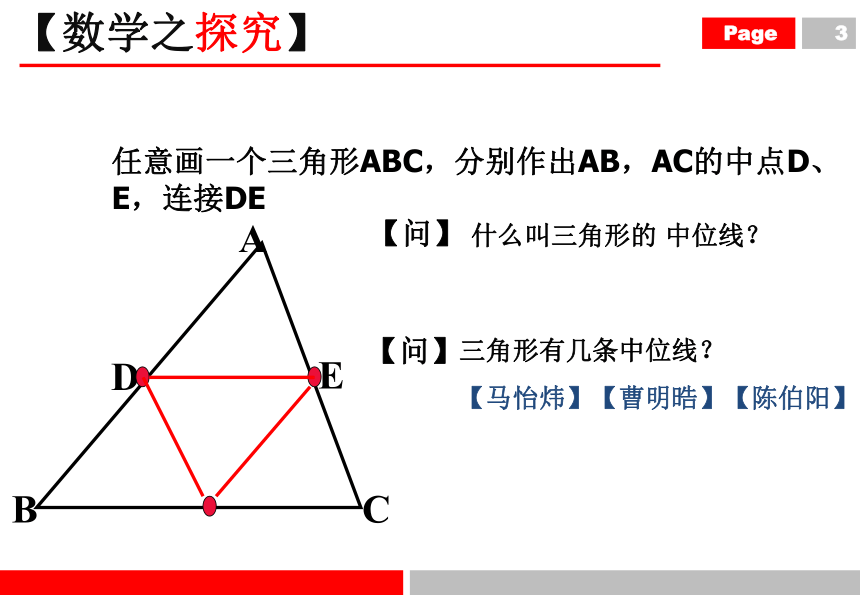
什么叫三角形的 中位线?
【问】
任意画一个三角形ABC,分别作出AB,AC的中点D、E,连接DE
【问】
三角形有几条中位线?
【马怡炜】【曹明晧】【陈伯阳】
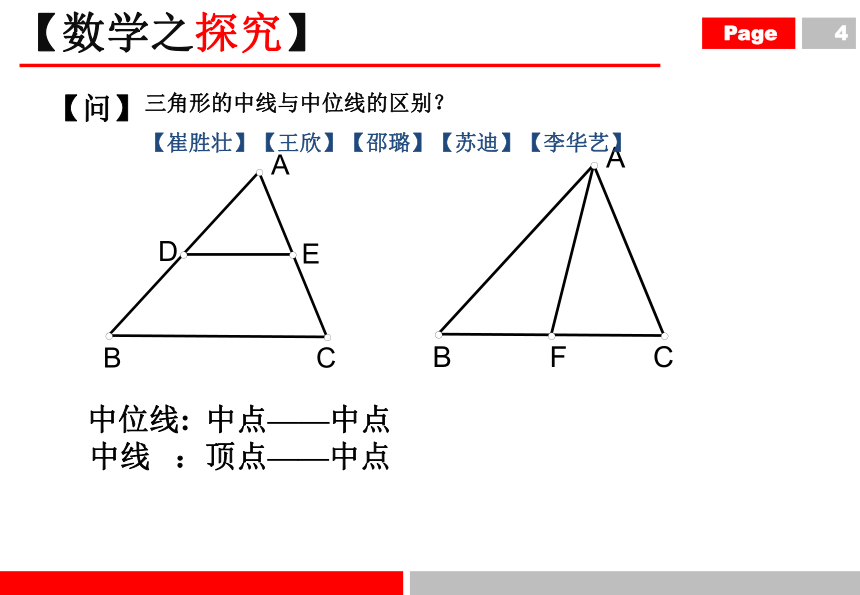
中位线: 中点——中点
中线 :顶点——中点
【问】
三角形的中线与中位线的区别?
【崔胜壮】【王欣】【邵璐】【苏迪】【李华艺】
*
Page
【数学之探究】
理解三角形的中位线定义的两层含义:
① 如果D、E分别为AB、AC的中点,那么DE为△ABC的 ;
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。
中位线
中点
*
Page
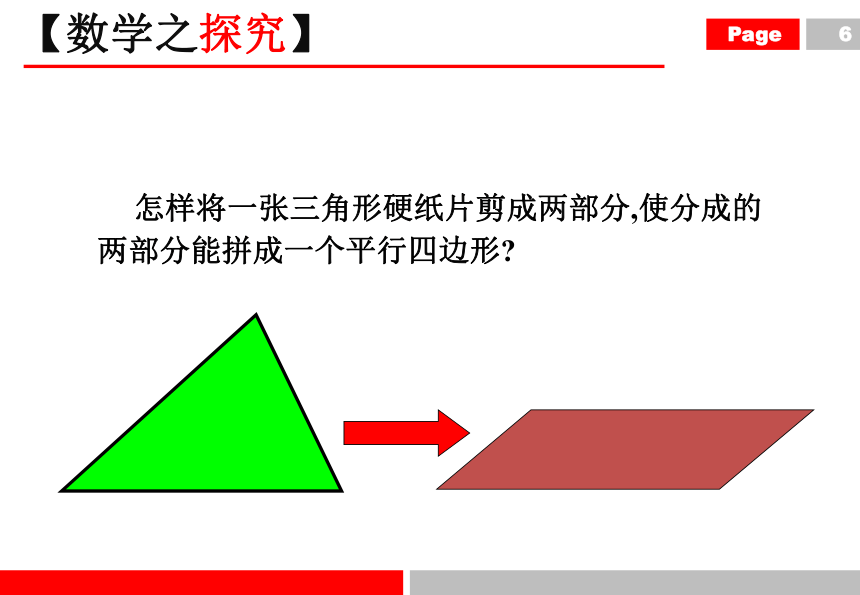
【数学之探究】
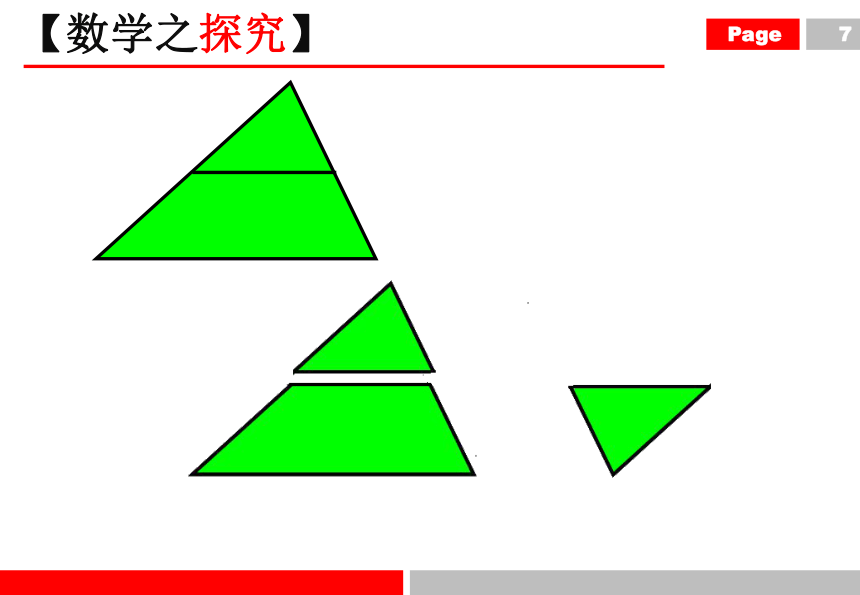
怎样将一张三角形硬纸片剪成两部分,使分成的两部分能拼成一个平行四边形
*
Page
【数学之探究】
【数学之探究】
*
Page
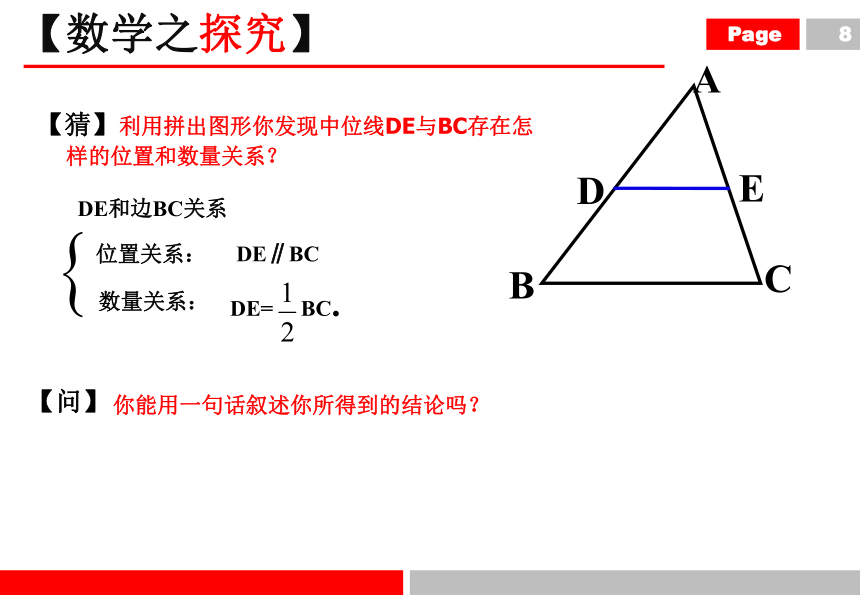
利用拼出图形你发现中位线DE与BC存在怎样的位置和数量关系?
DE和边BC关系
数量关系:
位置关系:
DE∥BC
A
B
C
D
E
DE= BC.
*
Page
【数学之探究】
【猜】
你能用一句话叙述你所得到的结论吗?
【问】
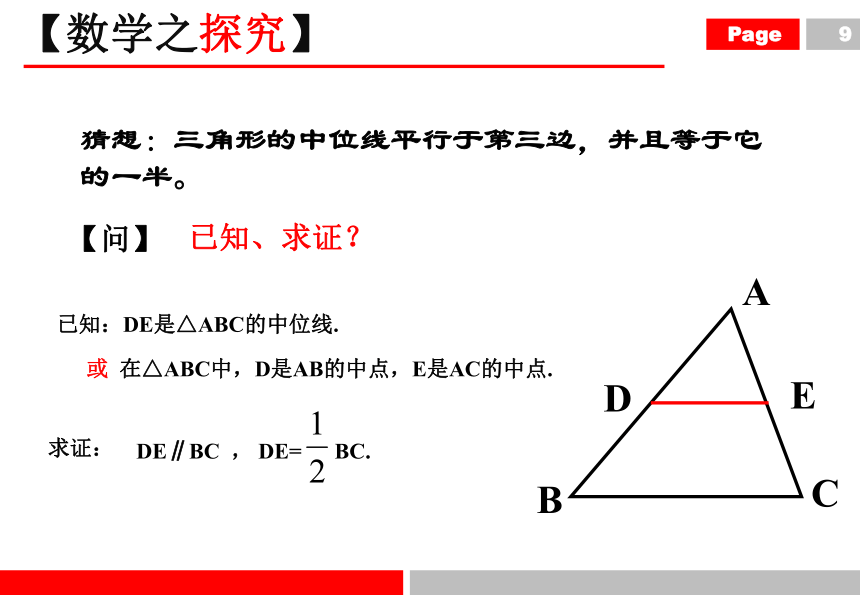
猜想:三角形的中位线平行于第三边,并且等于它的一半。
D
A
B
C
E
【问】
已知、求证?
已知:DE是△ABC的中位线.
或 在△ABC中,D是AB的中点,E是AC的中点.
求证:
DE∥BC , DE= BC.
*
Page
【数学之探究】
已知:在△ABC中,D是AB的中点,E是AC的中点。
求证:
DE∥BC,
DE= BC.
2
1
D
A
B
C
E
则有DE//BC,DE= DF= BC
A
B
C
F
*
Page
【数学之探究】
分析:
延长DE到F,使EF=DE , 连接CF
证△ADE △CFE,
得CF=AD ,∠A=∠FEC 得CF//AB
又可得CF=BD,CF//BD
所以四边形BCFD是平行四边形
≌
A
B
C
D
E
F
*
Page
【数学之探究】
证明:延长DE至点F,使DE=EF , 连接CF
即DE= DF
在△ADE和△CFE中
∴ △ADE △CFE (SAS)
∴ AD=CF,
∴ BD∥CF
∵AD=CF,AD=BD
∴ BD=CF
∴四边形DBCF是平行四边形
∴DE∥BC,DF=BC
即DE∥BC,DE= BC
小结:这种证明方法,是通过做辅助线将问题转化到平行四边形中去解决——转化思想
≌
三角形的中位线定理:三角形的中位线平行于第三边,并且等于它的一半
D
A
B
C
E
*
Page
【数学之探究】
用途:
证明平行问题
证明一条线段是另一条
线段的两倍或一半
符号语言:
∵DE是△ABC的中位线
∴ DE∥BC,DE= BC.
*
Page
个超1.如图1所示,EF是△ABC的中位线,若BC=8cm,则EF=_______cm.
个超2.三角形的三边长分别是3cm,5cm,6cm,则连结三边中点所围成的三角形的周长是_________cm.
图1
*
Page
【数学之用】
三条中位线围成的三角形周长与原三角形的周长
有什么关系?面积呢?【刘亚宁】【王欣】
*
Page
【数学之用】
【问】
A
B
C
D
E
4
7
F
3
5
7
Page
【数学之用】
*
个超6.如图所示,已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不变 D.以上说法都不对
做辅助线:
有中点连线而无三角形,作辅助线产生三角形
C
A
B
C
测出MN的长,就可知A、B两点的距离
M
N
在AB外选一点C,使C能直接到达A和B,
连结AC和BC,并分别找出AC和BC的中点M、N.
若MN=30 m,则AB=
2MN=60 m
如果,MN两点之间还有阻隔,你有什么解决办法?
【数学之用】
Page
*
【数学之趣】
Page
游戏
(1)任意画一个四边形ABCD
(2)取AB、BC、CD、DA的中点E、F、G、H
(3)顺次连接E、F、G、H
四边形EFGH是什么图形?
*
例1、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形。
A
B
C
D
E
F
G
H
聚焦解决问题
【数学之用】
Page
*
解:
连接AC,
在△ABC中,
∵ E、F分别是AB、BC边的中点,
∴EF是△ABC的中位线
∴ EF//AC,EF= AC
∴EF//HG,EF=HG
∴四边形EFGH是平行四边形
同理可得
HG//AC,HG= AC
结论:顺次连接任意四边形中点,得到平行四边形。
顺次连接任意四边形中点,得到一个
怎样的图形?【何如心】【祝嘉威】
【数学之用】
*
Page
个超7、已知:如图所示,在△ABC中,CF平分∠ACB,CA=CD,AE=EB.求证:EF= BD
学会了…的知识
掌握了…的方法
体会了…的思想
在同学身上学到了…
回顾学习活动形成自主反思
【数学之思】
Page
*
聚焦课堂收获
2、三角形的中位线定理
符号语言∵DE是△ABC的中位线
∴ DE∥BC,DE= BC.
用途: 为证明两线平行开辟了新思路
为解决线段倍分提供了新依据
方法上:辅助线
探究三角形中位线定理:三角形 平行四边边形
有中点连线而无三角形:作辅助线产生三角形
思想上:转化思想
1、三角形中位线的的定义
【数学之思】
聚焦课堂收获
Page
*
知识上:
*
Page
毕达哥拉斯
在数学天地里,重要的不是我们知道什么,而是我们怎么知道。
名人润泽课堂
【数学之思】
再 见
*
Page
6.4三角形的中位线定理
*
Page
聚焦质疑问题
小组合作交流:
1、从导学案中选出的5个问题和老师提的1个问题。
2、交流第6个问题时借助手中的三角形纸片。
【数学之问】
具体问题
1、 三角形的中线与中位线的区别?【崔胜壮】【王欣】【邵璐】【苏迪】【李华艺】
2、三角形有几条中位线?【马怡炜】【曹明晧】【陈伯阳】
3、三角形的三条中位线组成的三角形与原三角形的周长有什么关系?【刘亚宁】【王欣】
4、一个三角形的三条中位线分成的四个小三角形是否全等?【张继祖】
5、顺次连接任意四边形中点,得到一个怎样的图形?【何如心】【祝嘉威】
6、 怎样将一张三角形硬纸片剪成两部分,使分成的两部分能拼成一个平行四边形 【师】
A
B
C
D
E
*
Page
【数学之探究】
什么叫三角形的 中位线?
【问】
任意画一个三角形ABC,分别作出AB,AC的中点D、E,连接DE
【问】
三角形有几条中位线?
【马怡炜】【曹明晧】【陈伯阳】
中位线: 中点——中点
中线 :顶点——中点
【问】
三角形的中线与中位线的区别?
【崔胜壮】【王欣】【邵璐】【苏迪】【李华艺】
*
Page
【数学之探究】
理解三角形的中位线定义的两层含义:
① 如果D、E分别为AB、AC的中点,那么DE为△ABC的 ;
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。
中位线
中点
*
Page
【数学之探究】
怎样将一张三角形硬纸片剪成两部分,使分成的两部分能拼成一个平行四边形
*
Page
【数学之探究】
【数学之探究】
*
Page
利用拼出图形你发现中位线DE与BC存在怎样的位置和数量关系?
DE和边BC关系
数量关系:
位置关系:
DE∥BC
A
B
C
D
E
DE= BC.
*
Page
【数学之探究】
【猜】
你能用一句话叙述你所得到的结论吗?
【问】
猜想:三角形的中位线平行于第三边,并且等于它的一半。
D
A
B
C
E
【问】
已知、求证?
已知:DE是△ABC的中位线.
或 在△ABC中,D是AB的中点,E是AC的中点.
求证:
DE∥BC , DE= BC.
*
Page
【数学之探究】
已知:在△ABC中,D是AB的中点,E是AC的中点。
求证:
DE∥BC,
DE= BC.
2
1
D
A
B
C
E
则有DE//BC,DE= DF= BC
A
B
C
F
*
Page
【数学之探究】
分析:
延长DE到F,使EF=DE , 连接CF
证△ADE △CFE,
得CF=AD ,∠A=∠FEC 得CF//AB
又可得CF=BD,CF//BD
所以四边形BCFD是平行四边形
≌
A
B
C
D
E
F
*
Page
【数学之探究】
证明:延长DE至点F,使DE=EF , 连接CF
即DE= DF
在△ADE和△CFE中
∴ △ADE △CFE (SAS)
∴ AD=CF,
∴ BD∥CF
∵AD=CF,AD=BD
∴ BD=CF
∴四边形DBCF是平行四边形
∴DE∥BC,DF=BC
即DE∥BC,DE= BC
小结:这种证明方法,是通过做辅助线将问题转化到平行四边形中去解决——转化思想
≌
三角形的中位线定理:三角形的中位线平行于第三边,并且等于它的一半
D
A
B
C
E
*
Page
【数学之探究】
用途:
证明平行问题
证明一条线段是另一条
线段的两倍或一半
符号语言:
∵DE是△ABC的中位线
∴ DE∥BC,DE= BC.
*
Page
个超1.如图1所示,EF是△ABC的中位线,若BC=8cm,则EF=_______cm.
个超2.三角形的三边长分别是3cm,5cm,6cm,则连结三边中点所围成的三角形的周长是_________cm.
图1
*
Page
【数学之用】
三条中位线围成的三角形周长与原三角形的周长
有什么关系?面积呢?【刘亚宁】【王欣】
*
Page
【数学之用】
【问】
A
B
C
D
E
4
7
F
3
5
7
Page
【数学之用】
*
个超6.如图所示,已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不变 D.以上说法都不对
做辅助线:
有中点连线而无三角形,作辅助线产生三角形
C
A
B
C
测出MN的长,就可知A、B两点的距离
M
N
在AB外选一点C,使C能直接到达A和B,
连结AC和BC,并分别找出AC和BC的中点M、N.
若MN=30 m,则AB=
2MN=60 m
如果,MN两点之间还有阻隔,你有什么解决办法?
【数学之用】
Page
*
【数学之趣】
Page
游戏
(1)任意画一个四边形ABCD
(2)取AB、BC、CD、DA的中点E、F、G、H
(3)顺次连接E、F、G、H
四边形EFGH是什么图形?
*
例1、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形。
A
B
C
D
E
F
G
H
聚焦解决问题
【数学之用】
Page
*
解:
连接AC,
在△ABC中,
∵ E、F分别是AB、BC边的中点,
∴EF是△ABC的中位线
∴ EF//AC,EF= AC
∴EF//HG,EF=HG
∴四边形EFGH是平行四边形
同理可得
HG//AC,HG= AC
结论:顺次连接任意四边形中点,得到平行四边形。
顺次连接任意四边形中点,得到一个
怎样的图形?【何如心】【祝嘉威】
【数学之用】
*
Page
个超7、已知:如图所示,在△ABC中,CF平分∠ACB,CA=CD,AE=EB.求证:EF= BD
学会了…的知识
掌握了…的方法
体会了…的思想
在同学身上学到了…
回顾学习活动形成自主反思
【数学之思】
Page
*
聚焦课堂收获
2、三角形的中位线定理
符号语言∵DE是△ABC的中位线
∴ DE∥BC,DE= BC.
用途: 为证明两线平行开辟了新思路
为解决线段倍分提供了新依据
方法上:辅助线
探究三角形中位线定理:三角形 平行四边边形
有中点连线而无三角形:作辅助线产生三角形
思想上:转化思想
1、三角形中位线的的定义
【数学之思】
聚焦课堂收获
Page
*
知识上:
*
Page
毕达哥拉斯
在数学天地里,重要的不是我们知道什么,而是我们怎么知道。
名人润泽课堂
【数学之思】
再 见
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
