16.1 二次根式的概念及性质课件(26张PPT)
文档属性
| 名称 | 16.1 二次根式的概念及性质课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-20 21:23:30 | ||
图片预览





文档简介
课件26张PPT。(1)如左图所示,礼盒的上面是正方形,其面积为3,则它的边长是 .如果其面积为S,则它的边长是 .(2)如左图所示,一个长方形的围 栏,长是宽的2倍,面积为130m2,则它的宽为 m.(3)一个物体从高处自由落下,落到地面所用的时间t(单位:s)与开始落下时离地面的高度h(单位:m)满足关系式h=5t2.如果用含有h的式子表示t,那么t
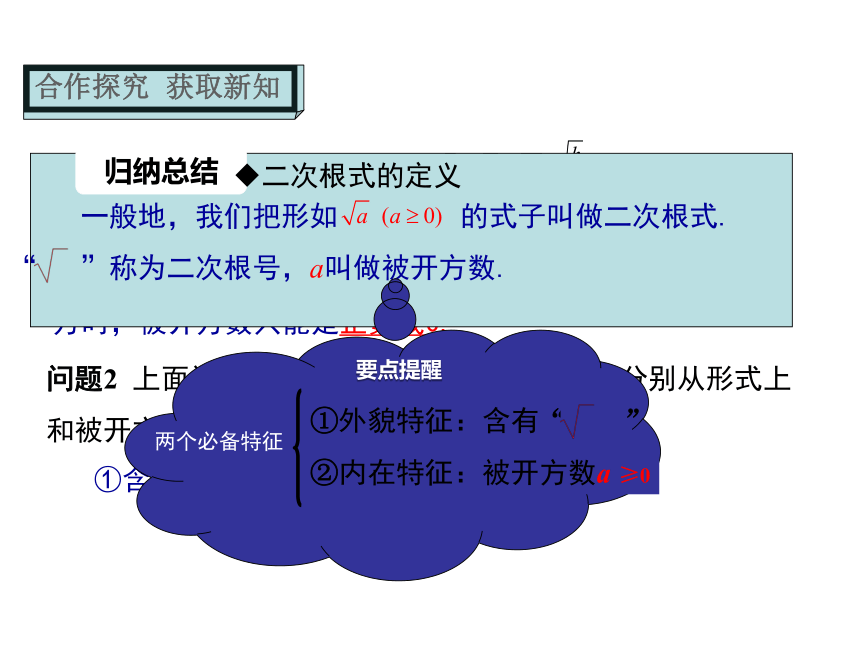
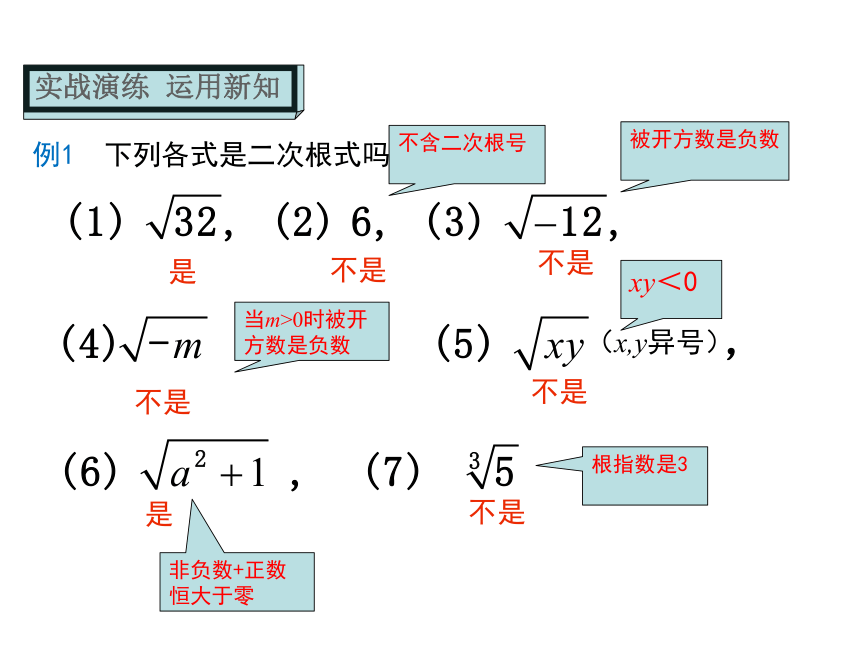
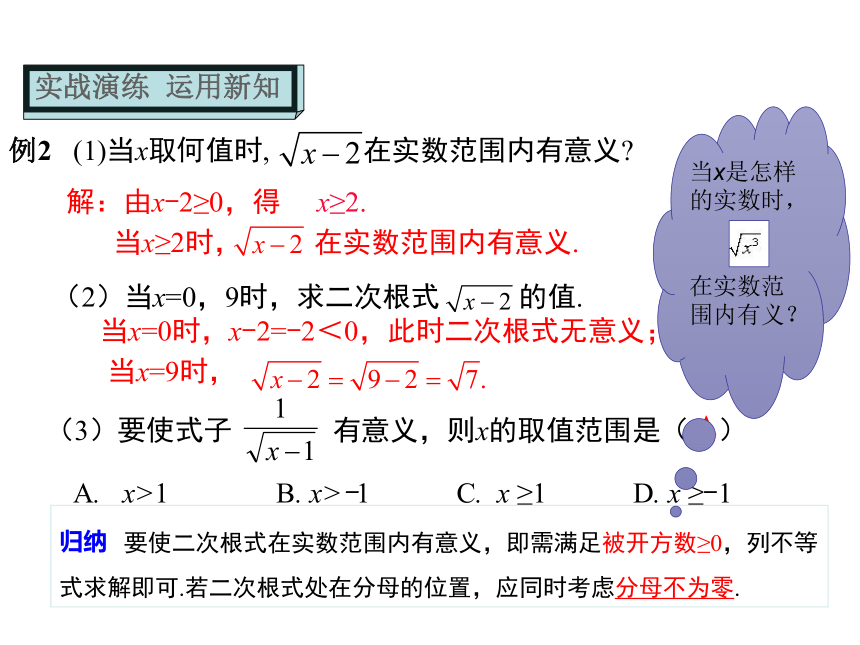
为 . 我们知道,负数没有平方根.因此,在实数范围内开平方时,被开方数只能是正数或0.②被开方数a ≥0例1 下列各式是二次根式吗?是不是不是不是不是是不是不含二次根号被开方数是负数当m>0时被开方数是负数xy<0非负数+正数恒大于零根指数是3解:由x-2≥0,得x≥2. 当x=9时,A. x>1 B. x>-1 C. x ≥1 D. x ≥-1A当x=0时,x-2=-2<0,此时二次根式无意义;思考解:(1)由题意可知a-2=0,b-3=0,c-4=0,解得a=2,b=3,c=4所以a-b+c=2-3+4=3;(2)由题意知,1-x≥0,且x-1≥0,联立解得x=1.从而知y=2016,所以x+2y=1+2×2016=4033.归纳总结
多个非负数的和为零,则可得每个非负数均为零.初中
阶段学过的非负数主要有绝对值、偶次幂及二次根式.
2.式子 有意义的条件是 ( ) A.x>2 B.x≥2 C.x<2 D.x≤23.若 是整数,则自然数n的值有 ( )
A.7个 B.8个 C.9个 D.10个D1. 下列式子中,不属于二次根式的是( )CA牛刀小试4.当a是怎样的实数时,下列各式在实数范围内有意义?5.要画一个面积为24cm2的长方形,使它的长与宽之比为3:2,它的长、宽各应是多少?解:设长方形的宽为xcm,根据得意得解得所以宽为4cm,长为6cm.(负值舍去).通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢?
问题1:你能将下列数字顺利通过下面两扇门吗? 问题2:两扇门交换位置,你还会走吗? 算术平方根之门 a≥0a为任意实数全部都能通过
算术平方根 平方运算 0
1
a(a≥0)观察:两者有什么关系?填一填:420活动1 :根据前面得出的结论填一填根据计算结果,你能把你的发现用字母表示出来吗?例1 计算: 解:想一想:此小题用到了幂的哪条基本性质呢?积的乘方:
(a b)2=a2b2
-4
0
1
-1
a填一填:平方运算算术平方根观察:
两者有什么关系?20.10活动2 :根据前面得出的结论填一填如何用字母表示你所得的公式呢?例3:化简解:你还有其他解法吗?归纳总结从运算顺序看从取值范围看从运算结果看先开方,后平方先平方,后开方a≥0a取任何实数a|a| 用基本运算符号(包括加、减、乘、除、乘方和开方)把_ 或 连接起来的式子,我们称这样的式子为代数式.数表示数的字母代数式的定义 想一想:到现在为止,初中阶段所学的代数式主要有哪几类?
1.化简 得( )
A. ±4 B. ±2 C. 4 D.-4C2.当1 A.3 B.-3 C.1 D.-1D3.化简:
(1) = ; (2) = ;
(3) ;(4) .3745.把下列非负数分别写成一个非负数的平方的形式:
(1) 9 ; (2)5 ; (3) 2.5 ;1通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢?
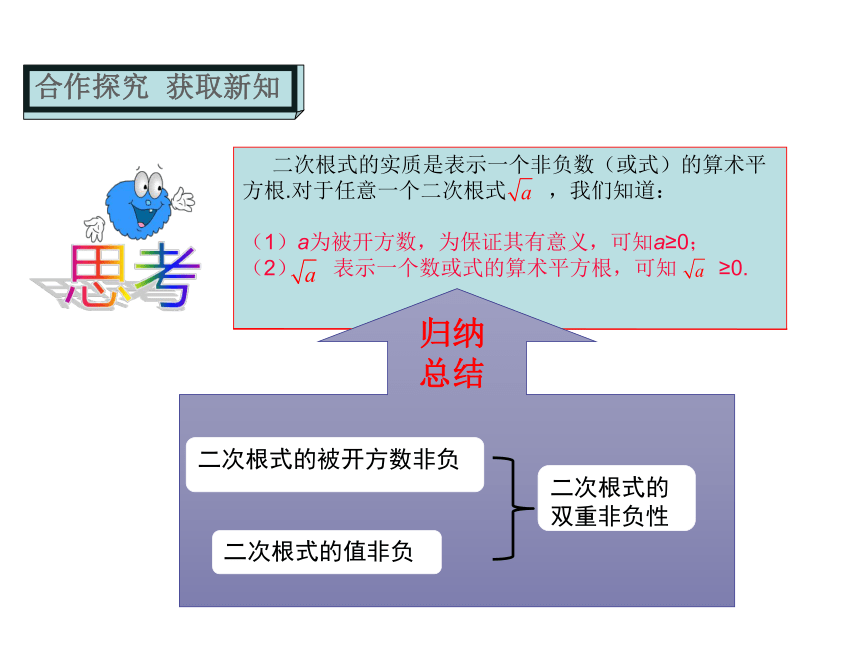
在有意义条件下求 字母的取值范围抓住被开方数必须为非负数,从而建立不等式求出其解集.二次根式的双重
非负性二
次
根
式二
次
根
式性
质拓
展
性
质
为 . 我们知道,负数没有平方根.因此,在实数范围内开平方时,被开方数只能是正数或0.②被开方数a ≥0例1 下列各式是二次根式吗?是不是不是不是不是是不是不含二次根号被开方数是负数当m>0时被开方数是负数xy<0非负数+正数恒大于零根指数是3解:由x-2≥0,得x≥2. 当x=9时,A. x>1 B. x>-1 C. x ≥1 D. x ≥-1A当x=0时,x-2=-2<0,此时二次根式无意义;思考解:(1)由题意可知a-2=0,b-3=0,c-4=0,解得a=2,b=3,c=4所以a-b+c=2-3+4=3;(2)由题意知,1-x≥0,且x-1≥0,联立解得x=1.从而知y=2016,所以x+2y=1+2×2016=4033.归纳总结
多个非负数的和为零,则可得每个非负数均为零.初中
阶段学过的非负数主要有绝对值、偶次幂及二次根式.
2.式子 有意义的条件是 ( ) A.x>2 B.x≥2 C.x<2 D.x≤23.若 是整数,则自然数n的值有 ( )
A.7个 B.8个 C.9个 D.10个D1. 下列式子中,不属于二次根式的是( )CA牛刀小试4.当a是怎样的实数时,下列各式在实数范围内有意义?5.要画一个面积为24cm2的长方形,使它的长与宽之比为3:2,它的长、宽各应是多少?解:设长方形的宽为xcm,根据得意得解得所以宽为4cm,长为6cm.(负值舍去).通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢?
问题1:你能将下列数字顺利通过下面两扇门吗? 问题2:两扇门交换位置,你还会走吗? 算术平方根之门 a≥0a为任意实数全部都能通过
算术平方根 平方运算 0
1
a(a≥0)观察:两者有什么关系?填一填:420活动1 :根据前面得出的结论填一填根据计算结果,你能把你的发现用字母表示出来吗?例1 计算: 解:想一想:此小题用到了幂的哪条基本性质呢?积的乘方:
(a b)2=a2b2
-4
0
1
-1
a填一填:平方运算算术平方根观察:
两者有什么关系?20.10活动2 :根据前面得出的结论填一填如何用字母表示你所得的公式呢?例3:化简解:你还有其他解法吗?归纳总结从运算顺序看从取值范围看从运算结果看先开方,后平方先平方,后开方a≥0a取任何实数a|a| 用基本运算符号(包括加、减、乘、除、乘方和开方)把_ 或 连接起来的式子,我们称这样的式子为代数式.数表示数的字母代数式的定义 想一想:到现在为止,初中阶段所学的代数式主要有哪几类?
1.化简 得( )
A. ±4 B. ±2 C. 4 D.-4C2.当1
(1) = ; (2) = ;
(3) ;(4) .3745.把下列非负数分别写成一个非负数的平方的形式:
(1) 9 ; (2)5 ; (3) 2.5 ;1通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢?
在有意义条件下求 字母的取值范围抓住被开方数必须为非负数,从而建立不等式求出其解集.二次根式的双重
非负性二
次
根
式二
次
根
式性
质拓
展
性
质
