6.9数学思考 课件(15张PPT)
图片预览





文档简介
(共15张PPT)
整理和复习
我们学过哪些数学思想和方法?
排列组合
集合
等量代换
数形结合
逻辑推理
统筹优化
数字编码
抽屉原理
……
一、引入情境,探究规律
(一)出示信息,明确问题
问题:你想怎样解决这个问题?动手试一试吧。
最多有2个点在同一条直线上,那么6个点可以连多少条线段?8个点呢?
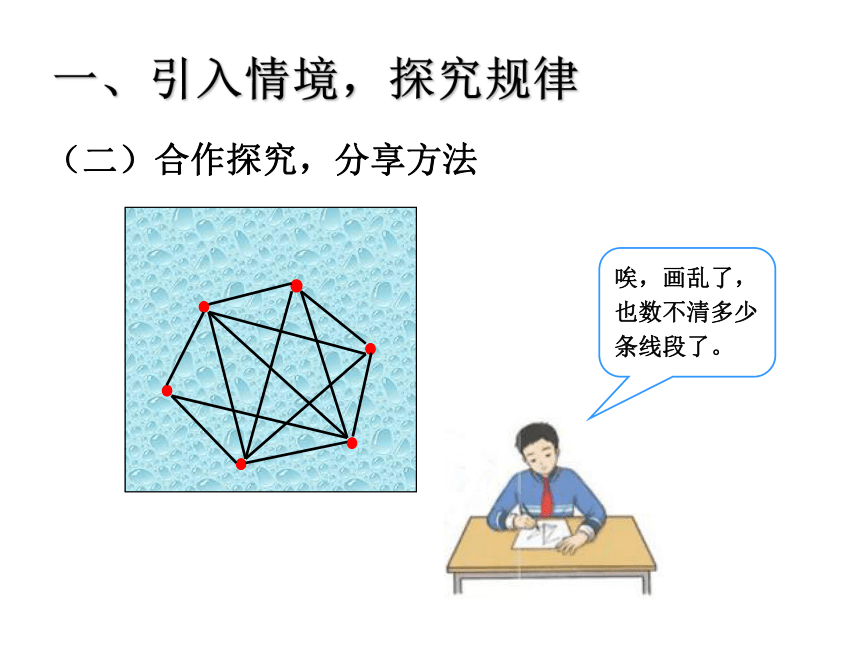
(二)合作探究,分享方法
一、引入情境,探究规律
唉,画乱了,也数不清多少条线段了。
不重复,不遗漏。
问题:想一想,按顺序画有什么好处?
5+4+3+2+1=15(条)
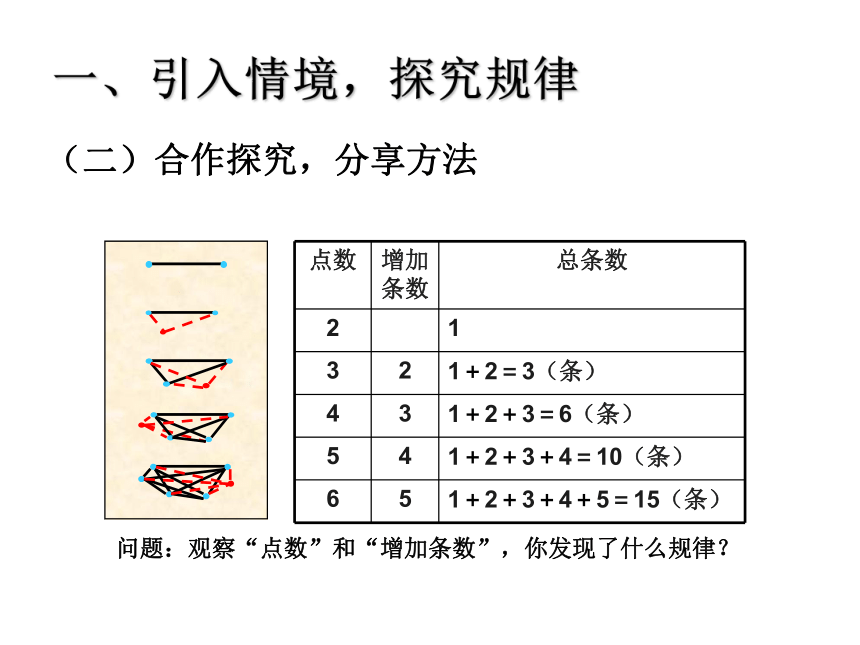
(二)合作探究,分享方法
一、引入情境,探究规律
别着急。
我来帮你!
(二)合作探究,分享方法
一、引入情境,探究规律
幸亏只有6个点,要是有600个点就惨了!
对呀,我们找找规律吧!从最少的2个点开始。
点数 增加条数 总条数
2 1
3 2 1+2=3(条)
4 3 1+2+3=6(条)
5 4 1+2+3+4=10(条)
6 5 1+2+3+4+5=15(条)
问题:观察“点数”和“增加条数”,你发现了什么规律?
(二)合作探究,分享方法
一、引入情境,探究规律
1+2+3+4+5+6+7
问题:1. 按照规律,8个点能连几条线段?
2. 为什么有8个点,列式却依次加到7呢?
(二)合作探究,分享方法
一、引入情境,探究规律
3. 想一想,能用简单方法计算吗?
=(1+7)+(2+6)+(3+5)+4
=28(条) ——8个点
=8×3+4
=(1+7)×7 ÷2
=28(条)
=8×7 ÷2
方法:几个连续自然数连加的和=(首项+末项)×项数÷2
1+2+3+4+5+6+7
二、应用规律,解决问题
=(1+11) × 11 ÷2
1+2+3+4+5+6+7+8+9+10+11
=66(条) ——12个点
=12×11 ÷ 2
1. 根据规律,你知道12个点、20个点能连多少条线段吗?
二、应用规律,解决问题
1. 根据规律,你知道12个点、20个点能连多少条线段吗?
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19
=(1+19) × 19 ÷2
=20×19 ÷2
=190(条) ——20个点
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
问题:1. 你想怎样解决这个问题?
2. 从最简单的数据开始,数一数每幅图各有多少个棋子?
三、巩固练习,提升认识
3. 在数的过程中,你发现了什么?
每行的棋子数×行数=棋子总数
1×1 2×2 3×3 4×4
1 4 9 16
问题:1. 第7幅图每行有几个棋子?有几行?共有几个棋子?
3. 第15幅图共有几个棋子?
三、巩固练习,提升认识
7×7=49(个)
15×15=225(个)
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
2. 每边的棋子数与图形的序号有什么关系?
观察下图,想一想。
(2)第n幅图有多少个棋子?
问题:第n幅图每边有多少个棋子?一共有多少个棋子?
三、巩固练习,提升认识
每行的棋子数×行数=棋子总数
n × n = 棋子总数
n2 =棋子总数
问题:遇到复杂的问题,你可以怎样思考?
三、巩固练习,提升认识
3. 有序思考
2. 画图、枚举
1. 化繁为简
4. 探究规律
整理和复习
我们学过哪些数学思想和方法?
排列组合
集合
等量代换
数形结合
逻辑推理
统筹优化
数字编码
抽屉原理
……
一、引入情境,探究规律
(一)出示信息,明确问题
问题:你想怎样解决这个问题?动手试一试吧。
最多有2个点在同一条直线上,那么6个点可以连多少条线段?8个点呢?
(二)合作探究,分享方法
一、引入情境,探究规律
唉,画乱了,也数不清多少条线段了。
不重复,不遗漏。
问题:想一想,按顺序画有什么好处?
5+4+3+2+1=15(条)
(二)合作探究,分享方法
一、引入情境,探究规律
别着急。
我来帮你!
(二)合作探究,分享方法
一、引入情境,探究规律
幸亏只有6个点,要是有600个点就惨了!
对呀,我们找找规律吧!从最少的2个点开始。
点数 增加条数 总条数
2 1
3 2 1+2=3(条)
4 3 1+2+3=6(条)
5 4 1+2+3+4=10(条)
6 5 1+2+3+4+5=15(条)
问题:观察“点数”和“增加条数”,你发现了什么规律?
(二)合作探究,分享方法
一、引入情境,探究规律
1+2+3+4+5+6+7
问题:1. 按照规律,8个点能连几条线段?
2. 为什么有8个点,列式却依次加到7呢?
(二)合作探究,分享方法
一、引入情境,探究规律
3. 想一想,能用简单方法计算吗?
=(1+7)+(2+6)+(3+5)+4
=28(条) ——8个点
=8×3+4
=(1+7)×7 ÷2
=28(条)
=8×7 ÷2
方法:几个连续自然数连加的和=(首项+末项)×项数÷2
1+2+3+4+5+6+7
二、应用规律,解决问题
=(1+11) × 11 ÷2
1+2+3+4+5+6+7+8+9+10+11
=66(条) ——12个点
=12×11 ÷ 2
1. 根据规律,你知道12个点、20个点能连多少条线段吗?
二、应用规律,解决问题
1. 根据规律,你知道12个点、20个点能连多少条线段吗?
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19
=(1+19) × 19 ÷2
=20×19 ÷2
=190(条) ——20个点
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
问题:1. 你想怎样解决这个问题?
2. 从最简单的数据开始,数一数每幅图各有多少个棋子?
三、巩固练习,提升认识
3. 在数的过程中,你发现了什么?
每行的棋子数×行数=棋子总数
1×1 2×2 3×3 4×4
1 4 9 16
问题:1. 第7幅图每行有几个棋子?有几行?共有几个棋子?
3. 第15幅图共有几个棋子?
三、巩固练习,提升认识
7×7=49(个)
15×15=225(个)
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
2. 每边的棋子数与图形的序号有什么关系?
观察下图,想一想。
(2)第n幅图有多少个棋子?
问题:第n幅图每边有多少个棋子?一共有多少个棋子?
三、巩固练习,提升认识
每行的棋子数×行数=棋子总数
n × n = 棋子总数
n2 =棋子总数
问题:遇到复杂的问题,你可以怎样思考?
三、巩固练习,提升认识
3. 有序思考
2. 画图、枚举
1. 化繁为简
4. 探究规律
