高中数学必修5 3.3.1二元一次不等式 组 与平面区域 课件 共23张PPT
文档属性
| 名称 | 高中数学必修5 3.3.1二元一次不等式 组 与平面区域 课件 共23张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 249.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-16 22:45:34 | ||
图片预览





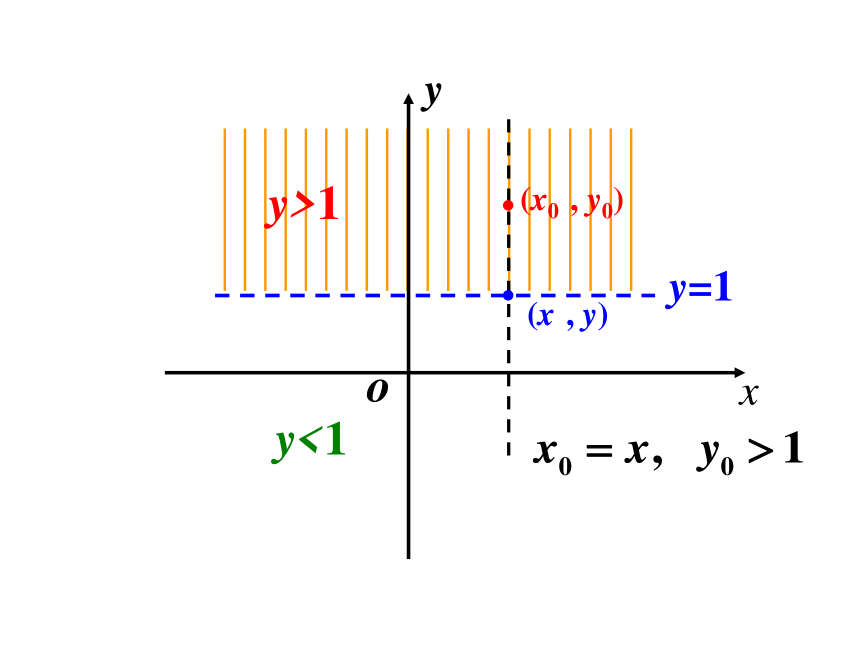

文档简介
课件23张PPT。3.3.13.3.1二元一次不等式(组)
与平面区域人教版·必修5·第三章《不等式》观察下列式子:
1、 2、
3、 4、
问题:你能试着给二元一次不等式和二元一次不等式组下定义吗?二元一次不等式和二元一次不等式组的定义 (1)二元一次不等式: 含有两个未知数,并且未知数的最高次数是1的
不等式叫做二元一次不等式 ;(2)二元一次不等式组: 由几个二元一次不等式组成的不等式组称为二元一次不等式组。 (4)二元一次不等式(组)的解集与平面直角
坐标系内的点之间的关系:二元一次不等式(组)的解集
可以看成是直角坐标系内的点构成的集合。满足二元一次不等式(组)的x和y的取值构成有序实数对(x,y),所有这样的有序实数对(x,y)构成的集合称为二元一次不等式(组)的解集。(3)二元一次不等式(组)的解集: 思考:那么,在直角坐标系内,二元一次不等式(组)的解集表示什么图形呢?一元一次不等式(组)的解集所表示的图形
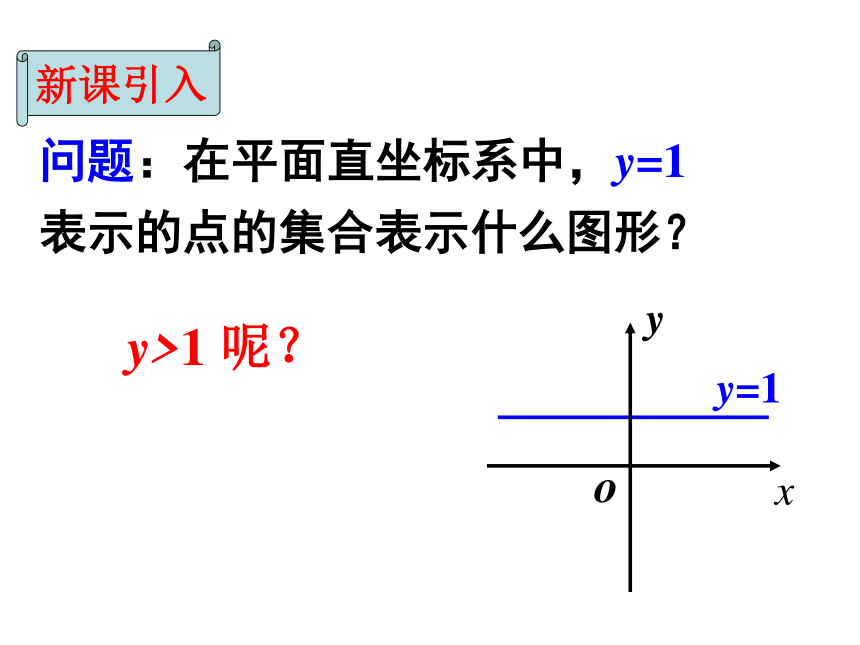
------数轴上的区间回忆:问题:在平面直坐标系中,y=1
表示的点的集合表示什么图形?
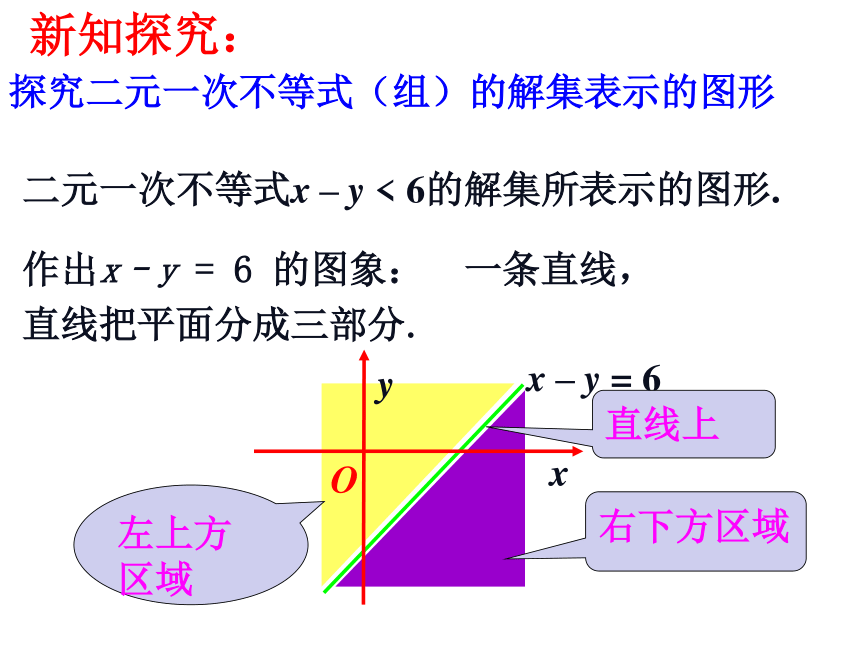
y>1 呢?新课引入y=1(x , y)(x0 , y0)y>1y<1新知探究: 探究二元一次不等式(组)的解集表示的图形 二元一次不等式x – y < 6的解集所表示的图形. 作出x–y = 6 的图象: 一条直线,
直线把平面分成三部分. 左上方区域右下方区域直线上 验证:设点P(x,y 1)是直线x – y = 6上的点,选取点
A(x,y 2),使它的坐标满足不等式x – y < 6,
请完成下面的表格, 新知探究:O新知探究: 当点A与点P有相同的横坐标时,它们的纵坐标有什么关
系?
直线x – y = 6左上方点的坐标与不等式x – y < 6有什么关系?
直线x – y = 6右下方点的坐标呢? O ( A点纵坐标大于P点纵坐标)(左上方点的坐标满足不等式)(右下方点的坐标不满足不等式)结论 不等式x – y < 6表示直线x – y = 6左上方的平面区域; 不等式x – y > 6表示直线x – y = 6右下方的平面区域; 直线叫做这两个区域的边界新知探究: 从特殊到一般情况: 二元一次不等式Ax + By + C>0在平面直角坐标系中表示直线Ax + By + C = 0某一侧所有点组成的平面区域。(虚线表示区域不包括边界直线) 注意:
若不等式中可以取等号,
则边界应画成实线,
否则应画成虚线。新知探究:如何判断二元一次不等式表示直线的哪一侧
平面区域?判断方法 由于直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同(同侧同号),所以只需在直线的某一侧取一个特殊点(x0,y0),根据Ax+By+C的正负即可判断Ax+By+C>0表示直线的哪一侧区域。
一般地 C≠0时,常把原点作为特殊点
C=0时,可取其他特殊点。
新知探究:例1:画出不等式 x + 4y < 4表示的平面区域 解:(1) 先画直线x + 4y – 4 = 0 (画成虚线) (2) 取原点(0,0),
代入x + 4y – 4,
∵0 + 4×0 – 4 = – 4 < 0∴原点在x + 4y – 4 < 0表示的平面区域内,不等式x + 4y – 4 < 0
表示的区域如图所示。特殊点定域例题分析分别在坐标系画出下列不等式表示的平面区域(1) x-y+5≥0(2) x+y≥0(3) x<3课堂练习1y=-3x+12x=2y此区域为所求二元一次不等式组表示平面区域:
是各个不等式所表示平面区域的公共部分. 画出不等式组 表示的平面区域所以黄色阴影部分即为所求。课堂练习2例3.一个化肥厂生产甲、乙两种混合肥料,
生产1车皮甲种肥料需用的主要原料是磷酸盐4吨,硝酸盐18吨;
生产1车皮乙种肥料需用的主要原料是磷酸盐1吨,硝酸盐15吨;
现有库存磷酸盐10吨,硝酸盐66吨.如果在此基础上进行生产,设x,y分别是计划生产甲、乙两种混合肥料的车皮数,请列出满足生产条件的数学关系式,并画出相应的平面区域. 解:设x,y分别是计划生产甲、乙两种混合肥料的车皮数,则x,y所满足的数学关系式为 分别画出不等式组中,各不等式所表示的区域. 然后取交集,就是不等式组所表示的区域。
1、二元一次不等式Ax+By+C>0(或<0)在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点 组成的平面区域。小结
小结课后作业
1.点A(3,1)和点B(-4,6)在直线
3x-2y+a=0的两侧,则( )
A.a<-7或a>24, B.-7C.a=-7或a=24, D.以上都不对
2.变式:如果同侧呢?
思考题
与平面区域人教版·必修5·第三章《不等式》观察下列式子:
1、 2、
3、 4、
问题:你能试着给二元一次不等式和二元一次不等式组下定义吗?二元一次不等式和二元一次不等式组的定义 (1)二元一次不等式: 含有两个未知数,并且未知数的最高次数是1的
不等式叫做二元一次不等式 ;(2)二元一次不等式组: 由几个二元一次不等式组成的不等式组称为二元一次不等式组。 (4)二元一次不等式(组)的解集与平面直角
坐标系内的点之间的关系:二元一次不等式(组)的解集
可以看成是直角坐标系内的点构成的集合。满足二元一次不等式(组)的x和y的取值构成有序实数对(x,y),所有这样的有序实数对(x,y)构成的集合称为二元一次不等式(组)的解集。(3)二元一次不等式(组)的解集: 思考:那么,在直角坐标系内,二元一次不等式(组)的解集表示什么图形呢?一元一次不等式(组)的解集所表示的图形
------数轴上的区间回忆:问题:在平面直坐标系中,y=1
表示的点的集合表示什么图形?
y>1 呢?新课引入y=1(x , y)(x0 , y0)y>1y<1新知探究: 探究二元一次不等式(组)的解集表示的图形 二元一次不等式x – y < 6的解集所表示的图形. 作出x–y = 6 的图象: 一条直线,
直线把平面分成三部分. 左上方区域右下方区域直线上 验证:设点P(x,y 1)是直线x – y = 6上的点,选取点
A(x,y 2),使它的坐标满足不等式x – y < 6,
请完成下面的表格, 新知探究:O新知探究: 当点A与点P有相同的横坐标时,它们的纵坐标有什么关
系?
直线x – y = 6左上方点的坐标与不等式x – y < 6有什么关系?
直线x – y = 6右下方点的坐标呢? O ( A点纵坐标大于P点纵坐标)(左上方点的坐标满足不等式)(右下方点的坐标不满足不等式)结论 不等式x – y < 6表示直线x – y = 6左上方的平面区域; 不等式x – y > 6表示直线x – y = 6右下方的平面区域; 直线叫做这两个区域的边界新知探究: 从特殊到一般情况: 二元一次不等式Ax + By + C>0在平面直角坐标系中表示直线Ax + By + C = 0某一侧所有点组成的平面区域。(虚线表示区域不包括边界直线) 注意:
若不等式中可以取等号,
则边界应画成实线,
否则应画成虚线。新知探究:如何判断二元一次不等式表示直线的哪一侧
平面区域?判断方法 由于直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同(同侧同号),所以只需在直线的某一侧取一个特殊点(x0,y0),根据Ax+By+C的正负即可判断Ax+By+C>0表示直线的哪一侧区域。
一般地 C≠0时,常把原点作为特殊点
C=0时,可取其他特殊点。
新知探究:例1:画出不等式 x + 4y < 4表示的平面区域 解:(1) 先画直线x + 4y – 4 = 0 (画成虚线) (2) 取原点(0,0),
代入x + 4y – 4,
∵0 + 4×0 – 4 = – 4 < 0∴原点在x + 4y – 4 < 0表示的平面区域内,不等式x + 4y – 4 < 0
表示的区域如图所示。特殊点定域例题分析分别在坐标系画出下列不等式表示的平面区域(1) x-y+5≥0(2) x+y≥0(3) x<3课堂练习1y=-3x+12x=2y此区域为所求二元一次不等式组表示平面区域:
是各个不等式所表示平面区域的公共部分. 画出不等式组 表示的平面区域所以黄色阴影部分即为所求。课堂练习2例3.一个化肥厂生产甲、乙两种混合肥料,
生产1车皮甲种肥料需用的主要原料是磷酸盐4吨,硝酸盐18吨;
生产1车皮乙种肥料需用的主要原料是磷酸盐1吨,硝酸盐15吨;
现有库存磷酸盐10吨,硝酸盐66吨.如果在此基础上进行生产,设x,y分别是计划生产甲、乙两种混合肥料的车皮数,请列出满足生产条件的数学关系式,并画出相应的平面区域. 解:设x,y分别是计划生产甲、乙两种混合肥料的车皮数,则x,y所满足的数学关系式为 分别画出不等式组中,各不等式所表示的区域. 然后取交集,就是不等式组所表示的区域。
1、二元一次不等式Ax+By+C>0(或<0)在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点 组成的平面区域。小结
小结课后作业
1.点A(3,1)和点B(-4,6)在直线
3x-2y+a=0的两侧,则( )
A.a<-7或a>24, B.-7
2.变式:如果同侧呢?
思考题
