人教版高中数学必修三课件:2.3 变量间的相关关系 共38张PPT
文档属性
| 名称 | 人教版高中数学必修三课件:2.3 变量间的相关关系 共38张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 431.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-16 22:49:31 | ||
图片预览








文档简介
课件38张PPT。基础知识框图表解变量间关系2.3变量间的相关关系一、变量之间的相关关系不同点:函数关系是一种确定的关系;而相关关系是一种非确定关系.相关关系与函数关系的异同点:相同点:均是指两个变量的关系.现实生活中存在许多相关关系,在下列两个变量的关系中,哪些是相关关系?
①正方形边长与面积之间的关系;
②作文水平与课外阅读量之间的关系;
③人的身高与体重之间的关系;
④人的身高与视力之间的关系;
⑤商品销售收入与广告支出经费之间的关系;
⑥粮食产量与施肥量之间的关系;
⑦匀速行驶的车辆的行驶距离与时间×××通过收集两个变量的大量数据,进行统计和数据分析,找出其中的规律,对其相关关系的程度作出一定判断.
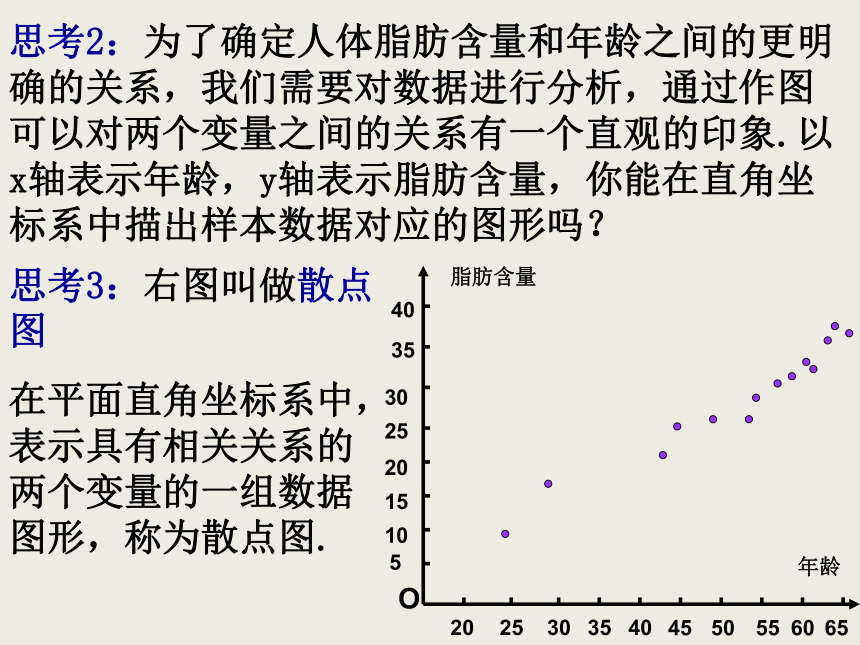
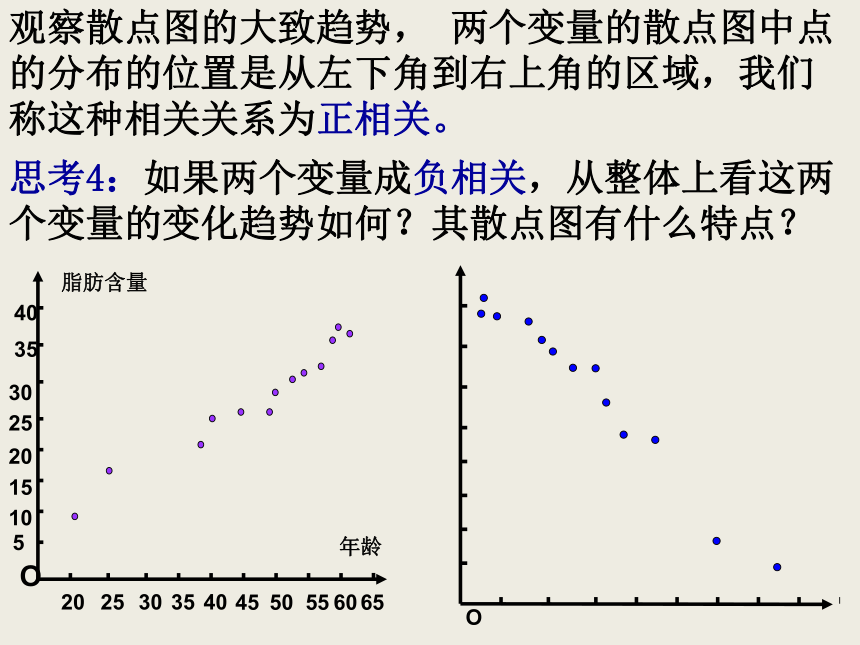
由于变量之间相关关系的广泛性和不确定性,所以样本数据应较大,和有代表性.才能对它们之间的关系作出正确的判断.如何判断两个变量之间是否具有相关关系以及相关程度的强弱探究:在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:其中各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均数.根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?思考1:对某一个人来说,他的体内脂肪含量不一定随年龄增长而增加或减少,但是如果把很多个体放在一起,就可能表现出一定的规律性.观察上表中的数据,大体上看,随着年龄的增加,人体脂肪含量怎样变化?思考2:为了确定人体脂肪含量和年龄之间的更明确的关系,我们需要对数据进行分析,通过作图可以对两个变量之间的关系有一个直观的印象.以x轴表示年龄,y轴表示脂肪含量,你能在直角坐标系中描出样本数据对应的图形吗? 思考3:右图叫做散点图在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图. 观察散点图的大致趋势, 两个变量的散点图中点
的分布的位置是从左下角到右上角的区域,我们称这种相关关系为正相关。思考4:如果两个变量成负相关,从整体上看这两个变量的变化趋势如何?其散点图有什么特点? 注:若两个变量散点图呈上图,则不具有相关关系。例1、以下是2000年某地搜集到的新房屋的销售价格和房屋的面积的数据:画出数据对应的散点图,并指出销售价格与房屋面积这两个变量是正相关还是负相关. 如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线就叫做回归直线。这条回归直线的方程,简称为回归方程。二、回归直线 只有散点图中的点呈条状集中在某一直线周围的时候,才可以说两个变量之间具有线性关系,才有两个变量的正线性相关和负线性相关的概念,才可以用回归直线来描述两个变量之间的关系三、如何具体的求出这个回归方程呢?求回归方程的关键是如何用数学的方法来刻画“从整体上看,各点与直线的偏差最小”。思考5:对一组具有线性相关关系的样本数据:(x1,y1),(x2,y2),…,(xn,yn),设其回归方
程为 ,可以用很多关系来刻画各样本点与回归直线的接近程度,我们经常使用样本数据的点到回归直线的距离的平方和最小来描述接近程度。这种方法叫最小二乘法。
通过最小二乘法得到的回归直线方程为:其中:
(其中,b是回归方程的斜率,a是截距)0.577×65-0.448= 37.1思考6:利用计算器或计算机可求得年龄和人体脂肪含量的样本数据的回归方程为
由此我们可以根据一个人的年龄预测其体内脂肪含量的百分比的回归值.若某人65岁,则其体内脂肪含量的百分比约为多少?能不能说他体内脂肪含量一定是37.1%?若某人65岁,可预测他体内脂肪含量在37.1%(0.577×65-0.448= 37.1%)附近的可能性比较大。但不能说他体内脂肪含量一定是37.1%原因:线性回归方程中的截距和斜率都是通过样本估计的,存在随机误差,这种误差可以导致预测结果的偏差,即使截距斜率没有误差,也不可
能百分百地保证对应于x,预报值 能等于实际值y例2、(07广东)下表提供了某厂节油降耗技术发行后生产甲产品过程中记录的产量(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
X 3 4 5 6
y2.5 3 4 4.5
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y= ;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
所求的回归方程为 (2)解:(3) 预测生产100吨甲产品的生产能耗比技改前降
低 (吨) 例2、有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:1、画出散点图;
2、从散点图中发现气温与热饮销售杯数之间关系的一般规律;
3、求回归方程;
4、如果某天的气温是2摄氏度,预测这天卖出的热饮杯数。1、散点图2、从图3-1看到,各点散布在从左上角到由下角的区域里,因此,气温与热饮销售杯数之间成负相关,即气温越高,卖出去的热饮杯数越少。3、从散点图可以看出,这些点大致分布在一条直线的附近,因此利用公式1求出回归方程的系数。Y= -2.352x+147.7674、当x=2时,Y=143.063 因此,某天的气温为2摄氏度时,这天大约可以卖出143杯热饮。本节重点知识回顾1、相关关系
(1)概念:自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫相关关系。
(2)相关关系与函数关系的异同点。
相同点:两者均是指两个变量间的关系。
不同点:函数关系是一种确定关系,是一种因果系;相关关系是一种非确定的关系,也不一定是因果关系(但可能是伴随关系)。
(3)相关关系的分析方向。
在收集大量数据的基础上,利用统计分析,发现规律,对它们的关系作出判断。2、两个变量的线性相关 (1)回归分析
对具有相关关系的两个变量进行统计分析的方法叫回归分析。通俗地讲,回归分析是寻找相关关系中非确定关系的某种确定性。 (2)散点图
A、定义;B、正相关、负相关。 3、回归直线方程 注:如果关于两个变量统计数据的散点图呈现发散状,则这两个变量之间不具有相关关系.3、回归直线方程 (1)回归直线:观察散点图的特征,如果各点大致分布在一条直线的附近,就称两个变量之间具有线性相关的关系,这条直线叫做回归直线。(2)最小二乘法(3)利用回归直线对总体进行估计练习2-1、 观察两相关量得如下数据:求两变量间的回归方程.解:列表:计算得:所求回归直线方程为注意:求回归直线方程的步骤:第一步:列表第二步:计算:第三步:代入公式计算b,a的值第四步:列出直线方程。练习2-2、:给出施化肥量对水稻产量
影响的试验数据:(1)画出上表的散点图;
(2)求出回归直线并且画出图形. 从而得回归直线方程是 解:(1)散点图(略).
(2)表中的数据进行具体计算,列成以下表格.(图形略)故可得到4、利用回归直线方程对总体进行估计练习2-3、炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系。如果已测得炉料熔化完毕时,钢水的含碳量X与冶炼时间y(从炉料熔化完毕到出刚的时间)的一列数据,如下表所示:(1)作出散点图,找规律。
(2)求回归直线方程。
(3)预测当钢水含碳量为160时,应冶炼多少分钟?解: (1) 作散点图.从图可以看出,各点分布在一条直线附近,即它们线形相关.(2)列出下表,并计算设所求的回归直线方程为其中a,b的值使的值最小.所以回归直线的方程为 =1.267x-30.51(3)当x=160时, 1.267.160-30.51=172归纳:1.求样本数据的线性回归方程,可按下列步骤进行:第一步,计算平均数 , 第二步,求和 , (列表) 第三步,计算 第四步,写出回归方程 2.回归方程被样本数据惟一确定,各样本点大致分布在回归直线附近.对同一个总体,不同的样本数据对应不同的回归直线,所以回归直线也具有随机性. 3.对于任意一组样本数据,利用上述公式都可以求得“回归方程”,如果这组数据不具有线性相关关系,即不存在回归直线,那么所得的“回归方程”是没有实际意义的.因此,对一组样本数据,应先作散点图,在具有线性相关关系的前提下再求回归方程.整体上最接近 方案一:采用测量的方法:先画一条直线,测量出各点到它的距离,然后移动直线,到达一个使距离之和最小的位置,测量出此时直线的斜率和截距,就得到回归方程。三、如何具体的求出这个回归方程呢?方案二: 在图中选取两点画直线,使得直线两侧的点的个数基本相同。三、如何具体的求出这个回归方程呢?方案三: 在散点图中多取几组点,确定几条直线的方程,分别求出各条直线的斜率和截距的平均数,将这两个平均数作为回归方程的斜率和截距。三、如何具体的求出这个回归方程呢? 以上公式的推导较复杂,故不作推导,但它的原理较为简单:即各点到该直线的距离的平方和最小,这一方法叫最小二乘法。(参看如书P88-P89)
①正方形边长与面积之间的关系;
②作文水平与课外阅读量之间的关系;
③人的身高与体重之间的关系;
④人的身高与视力之间的关系;
⑤商品销售收入与广告支出经费之间的关系;
⑥粮食产量与施肥量之间的关系;
⑦匀速行驶的车辆的行驶距离与时间×××通过收集两个变量的大量数据,进行统计和数据分析,找出其中的规律,对其相关关系的程度作出一定判断.
由于变量之间相关关系的广泛性和不确定性,所以样本数据应较大,和有代表性.才能对它们之间的关系作出正确的判断.如何判断两个变量之间是否具有相关关系以及相关程度的强弱探究:在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:其中各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均数.根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?思考1:对某一个人来说,他的体内脂肪含量不一定随年龄增长而增加或减少,但是如果把很多个体放在一起,就可能表现出一定的规律性.观察上表中的数据,大体上看,随着年龄的增加,人体脂肪含量怎样变化?思考2:为了确定人体脂肪含量和年龄之间的更明确的关系,我们需要对数据进行分析,通过作图可以对两个变量之间的关系有一个直观的印象.以x轴表示年龄,y轴表示脂肪含量,你能在直角坐标系中描出样本数据对应的图形吗? 思考3:右图叫做散点图在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图. 观察散点图的大致趋势, 两个变量的散点图中点
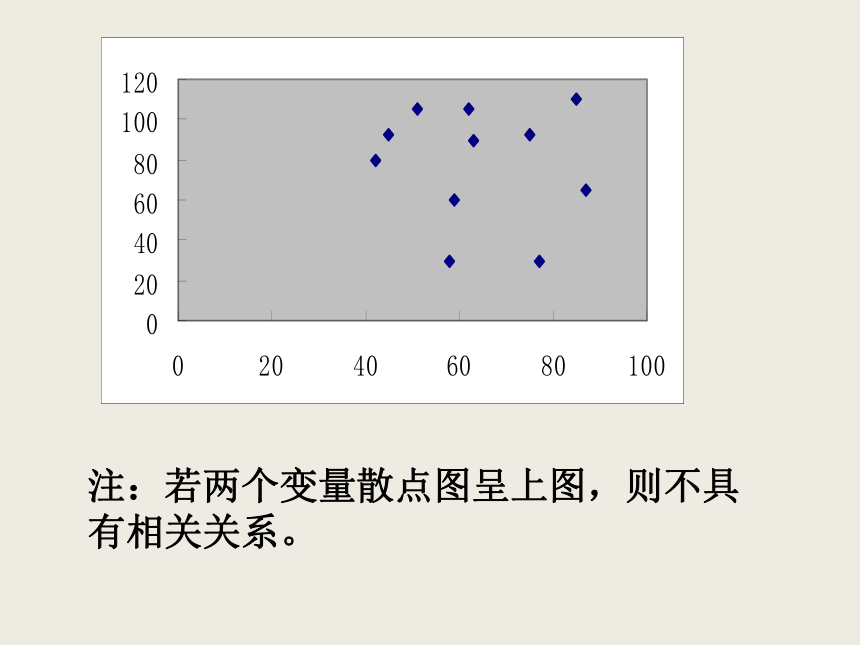
的分布的位置是从左下角到右上角的区域,我们称这种相关关系为正相关。思考4:如果两个变量成负相关,从整体上看这两个变量的变化趋势如何?其散点图有什么特点? 注:若两个变量散点图呈上图,则不具有相关关系。例1、以下是2000年某地搜集到的新房屋的销售价格和房屋的面积的数据:画出数据对应的散点图,并指出销售价格与房屋面积这两个变量是正相关还是负相关. 如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线就叫做回归直线。这条回归直线的方程,简称为回归方程。二、回归直线 只有散点图中的点呈条状集中在某一直线周围的时候,才可以说两个变量之间具有线性关系,才有两个变量的正线性相关和负线性相关的概念,才可以用回归直线来描述两个变量之间的关系三、如何具体的求出这个回归方程呢?求回归方程的关键是如何用数学的方法来刻画“从整体上看,各点与直线的偏差最小”。思考5:对一组具有线性相关关系的样本数据:(x1,y1),(x2,y2),…,(xn,yn),设其回归方
程为 ,可以用很多关系来刻画各样本点与回归直线的接近程度,我们经常使用样本数据的点到回归直线的距离的平方和最小来描述接近程度。这种方法叫最小二乘法。
通过最小二乘法得到的回归直线方程为:其中:
(其中,b是回归方程的斜率,a是截距)0.577×65-0.448= 37.1思考6:利用计算器或计算机可求得年龄和人体脂肪含量的样本数据的回归方程为
由此我们可以根据一个人的年龄预测其体内脂肪含量的百分比的回归值.若某人65岁,则其体内脂肪含量的百分比约为多少?能不能说他体内脂肪含量一定是37.1%?若某人65岁,可预测他体内脂肪含量在37.1%(0.577×65-0.448= 37.1%)附近的可能性比较大。但不能说他体内脂肪含量一定是37.1%原因:线性回归方程中的截距和斜率都是通过样本估计的,存在随机误差,这种误差可以导致预测结果的偏差,即使截距斜率没有误差,也不可
能百分百地保证对应于x,预报值 能等于实际值y例2、(07广东)下表提供了某厂节油降耗技术发行后生产甲产品过程中记录的产量(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
X 3 4 5 6
y2.5 3 4 4.5
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y= ;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
所求的回归方程为 (2)解:(3) 预测生产100吨甲产品的生产能耗比技改前降
低 (吨) 例2、有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:1、画出散点图;
2、从散点图中发现气温与热饮销售杯数之间关系的一般规律;
3、求回归方程;
4、如果某天的气温是2摄氏度,预测这天卖出的热饮杯数。1、散点图2、从图3-1看到,各点散布在从左上角到由下角的区域里,因此,气温与热饮销售杯数之间成负相关,即气温越高,卖出去的热饮杯数越少。3、从散点图可以看出,这些点大致分布在一条直线的附近,因此利用公式1求出回归方程的系数。Y= -2.352x+147.7674、当x=2时,Y=143.063 因此,某天的气温为2摄氏度时,这天大约可以卖出143杯热饮。本节重点知识回顾1、相关关系
(1)概念:自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫相关关系。
(2)相关关系与函数关系的异同点。
相同点:两者均是指两个变量间的关系。
不同点:函数关系是一种确定关系,是一种因果系;相关关系是一种非确定的关系,也不一定是因果关系(但可能是伴随关系)。
(3)相关关系的分析方向。
在收集大量数据的基础上,利用统计分析,发现规律,对它们的关系作出判断。2、两个变量的线性相关 (1)回归分析
对具有相关关系的两个变量进行统计分析的方法叫回归分析。通俗地讲,回归分析是寻找相关关系中非确定关系的某种确定性。 (2)散点图
A、定义;B、正相关、负相关。 3、回归直线方程 注:如果关于两个变量统计数据的散点图呈现发散状,则这两个变量之间不具有相关关系.3、回归直线方程 (1)回归直线:观察散点图的特征,如果各点大致分布在一条直线的附近,就称两个变量之间具有线性相关的关系,这条直线叫做回归直线。(2)最小二乘法(3)利用回归直线对总体进行估计练习2-1、 观察两相关量得如下数据:求两变量间的回归方程.解:列表:计算得:所求回归直线方程为注意:求回归直线方程的步骤:第一步:列表第二步:计算:第三步:代入公式计算b,a的值第四步:列出直线方程。练习2-2、:给出施化肥量对水稻产量
影响的试验数据:(1)画出上表的散点图;
(2)求出回归直线并且画出图形. 从而得回归直线方程是 解:(1)散点图(略).
(2)表中的数据进行具体计算,列成以下表格.(图形略)故可得到4、利用回归直线方程对总体进行估计练习2-3、炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系。如果已测得炉料熔化完毕时,钢水的含碳量X与冶炼时间y(从炉料熔化完毕到出刚的时间)的一列数据,如下表所示:(1)作出散点图,找规律。
(2)求回归直线方程。
(3)预测当钢水含碳量为160时,应冶炼多少分钟?解: (1) 作散点图.从图可以看出,各点分布在一条直线附近,即它们线形相关.(2)列出下表,并计算设所求的回归直线方程为其中a,b的值使的值最小.所以回归直线的方程为 =1.267x-30.51(3)当x=160时, 1.267.160-30.51=172归纳:1.求样本数据的线性回归方程,可按下列步骤进行:第一步,计算平均数 , 第二步,求和 , (列表) 第三步,计算 第四步,写出回归方程 2.回归方程被样本数据惟一确定,各样本点大致分布在回归直线附近.对同一个总体,不同的样本数据对应不同的回归直线,所以回归直线也具有随机性. 3.对于任意一组样本数据,利用上述公式都可以求得“回归方程”,如果这组数据不具有线性相关关系,即不存在回归直线,那么所得的“回归方程”是没有实际意义的.因此,对一组样本数据,应先作散点图,在具有线性相关关系的前提下再求回归方程.整体上最接近 方案一:采用测量的方法:先画一条直线,测量出各点到它的距离,然后移动直线,到达一个使距离之和最小的位置,测量出此时直线的斜率和截距,就得到回归方程。三、如何具体的求出这个回归方程呢?方案二: 在图中选取两点画直线,使得直线两侧的点的个数基本相同。三、如何具体的求出这个回归方程呢?方案三: 在散点图中多取几组点,确定几条直线的方程,分别求出各条直线的斜率和截距的平均数,将这两个平均数作为回归方程的斜率和截距。三、如何具体的求出这个回归方程呢? 以上公式的推导较复杂,故不作推导,但它的原理较为简单:即各点到该直线的距离的平方和最小,这一方法叫最小二乘法。(参看如书P88-P89)
