苏教版高中数学选修2-1课件:第二章 圆锥曲线与方程 共19张PPT
文档属性
| 名称 | 苏教版高中数学选修2-1课件:第二章 圆锥曲线与方程 共19张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-16 22:53:23 | ||
图片预览




文档简介
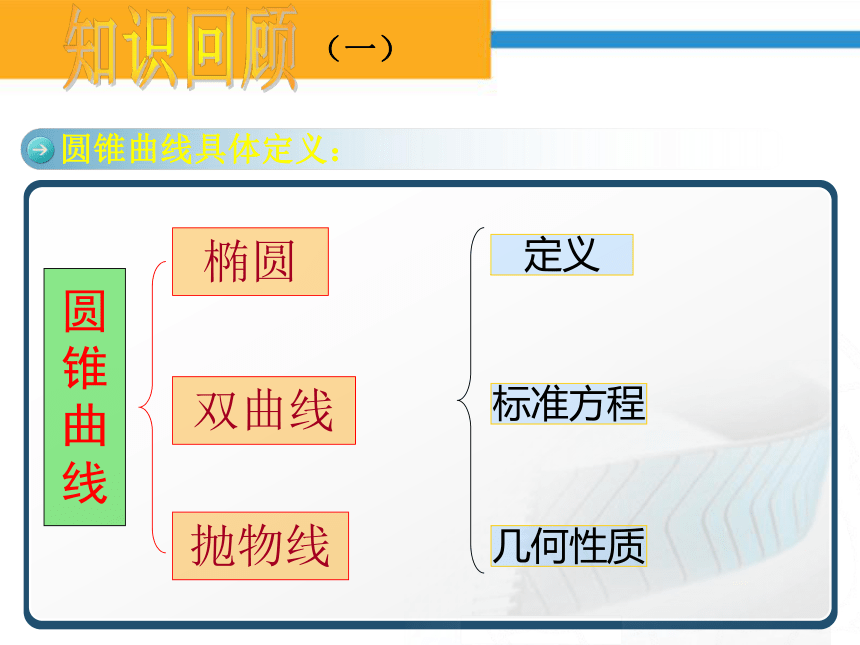
课件19张PPT。圆锥曲线与方程主要考查的内容: 知识回顾圆锥曲线具体定义:(一)知识回顾(一)圆
锥
曲
线椭圆双曲线抛物线定义标准方程几何性质知识回顾(二)双曲线的定义: 平面内到两个定点F1、F2的距离之和等于常数 (大于F1F2 )的点的轨迹被叫为椭圆。 知识回顾(二)可以用表达式 来表示。 平面内到两个定点F1、F2距离差的绝对值等于
常数(小于F1F2 )的点的轨迹叫做双曲线。
可用表达式 表示。抛物线的定义:平面内到一个定点F和一条定直线 l(F不在l上)
的距离相等的点的轨迹叫做抛物线.
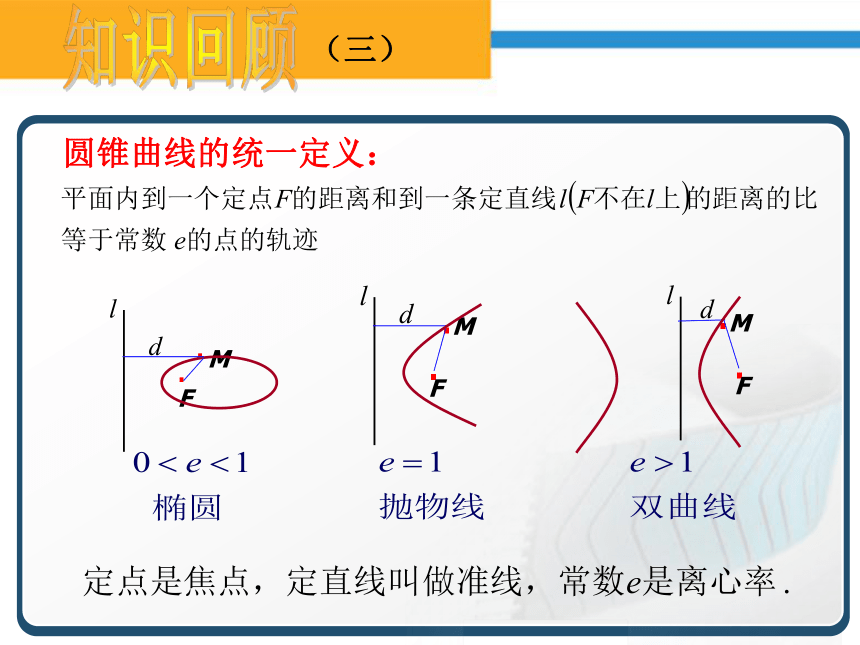
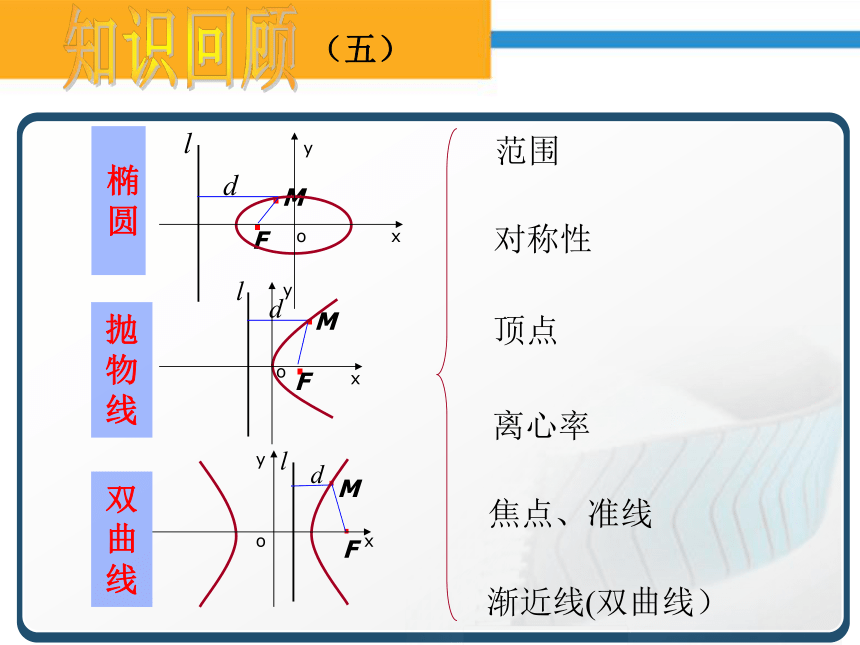
可用表达式 MF=d 表示,其中d为F到l的距离.椭圆的定义:知识回顾(三)知识回顾(三)圆锥曲线的统一定义:知识回顾(四)椭圆的标准方程:双曲线的标准方程:抛物线的标准方程:知识回顾(四)知识回顾(五) 椭
圆抛
物
线双
曲
线知识回顾(五)yxoyxoyxo知识回顾(六)知识回顾(六)01(0,0) e=1关于x、y轴、原点对称关于x、y轴、原点对称关于x轴对称基础训练基础训练1、2、3基础训练基础训练4、5、64(0,-1)基础训练基础训练7、8小结:要熟练掌握圆锥曲线的基础知识,以解决基本问题。典型例题典型例题1【例1】已知椭圆的中心在原点,焦点在坐标轴上,又过点
P(3,2),长轴长是短轴长的3倍,求该椭圆的方程。 解:由题知,椭圆的方程为标准方程。 小结:本题用待定系数法求椭圆的标准方程,
但在无法判断焦点所在的坐标轴时,要分情况讨论 解: 依题意,双曲线焦点在y轴上,半焦距c=10,典型例题典型例题2【例2】 已知双曲线的中心在坐标原点,一个焦点为F(0,10),两条渐近线的方程为 ,求该双曲线的标准方程.小结:本题是利用渐近线方程、a,b,c三者之间的
关系,求解双曲线方程可设标准方程为为 ,故双曲线方程为又渐近线方程故典型例题【例3】已知抛物线C的顶点在原点,焦点F在x轴的正半轴上,
设A、B是抛物线C上的两个动点(AB不垂直于x轴),
且AF+BF=8,线段AB的垂直平分线恒经过点Q(6、0),求此抛物线方程。 典型例题3典型例题典型例题3【例3】已知抛物线C的顶点在原点,焦点F在x轴的正半轴上,
设A、B是抛物线C上的两个动点(AB不垂直于x轴),
且AF+BF=8,线段AB的垂直平分线恒经过点Q(6、0),求此抛物线方程。 小结:抛物线的标准方程有四种形式,用待定系数法求解是最基本的方法。
本题是综合抛物线的定义及中垂线的有关知识解题。 解:典型例题典型例题4【例4】 (2009·江苏)如图所示,在平面直角坐标系xOy中,A1,A2,B1,B2为椭圆 (a>b>0)的四个顶点,F为其右焦点,直线A1B2与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,求该椭圆的离心率.
解 由题意结合图形得,
即-bx+ay=ab, ①
即bx-cy=bc, ② 由①②求得:典型例题典型例题4【例4】 (2009·江苏)如图所示,在平面直角坐标系xOy中,A1,A2,B1,B2为椭圆 (a>b>0)的四个顶点,F为其右焦点,直线A1B2与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,求该椭圆的离心率.
解:
(续)即4c2+a2+2ac+c2=4a2-8ac+4c2,
c2+10ac-3a2=0,∴e2+10e-3=0.
又∵0小结:本题综合了直线和椭圆的定义、离心率等几何性质,
体现了方程的思想。 变式训练变式训练 已知双曲线 (a>0,b>0)的左、右焦点分别为F1、
F2,点P在右支上,|PF1|=4|PF2|,求双曲线离心率e的最大值.解 方法一 在△PF1F2中,cos∠F1PF2= ,要求e的最大值,只须求cos∠F1PF2的最小值,
当cos∠F1PF2=-1时e最大值为 .变式训练变式训练 已知双曲线 (a>0,b>0)的左、右焦点分别为F1、
F2,点P在右支上,|PF1|=4|PF2|,求双曲线离心率e的最大值.
方法二 由以上可知小结:本题考查了双曲线的两种定义形式,熟练运用
定义解题是基本思路。 课堂小结 本节课主要复习圆锥曲线的定义、标准方程、
几何性质及应用,同时注重与其他知识的综合
运用,在解题时除了要熟练掌握圆锥曲线基本知
识外,需注重利用数形结合思想解决实际问题。
课堂小结
锥
曲
线椭圆双曲线抛物线定义标准方程几何性质知识回顾(二)双曲线的定义: 平面内到两个定点F1、F2的距离之和等于常数 (大于F1F2 )的点的轨迹被叫为椭圆。 知识回顾(二)可以用表达式 来表示。 平面内到两个定点F1、F2距离差的绝对值等于
常数(小于F1F2 )的点的轨迹叫做双曲线。
可用表达式 表示。抛物线的定义:平面内到一个定点F和一条定直线 l(F不在l上)
的距离相等的点的轨迹叫做抛物线.
可用表达式 MF=d 表示,其中d为F到l的距离.椭圆的定义:知识回顾(三)知识回顾(三)圆锥曲线的统一定义:知识回顾(四)椭圆的标准方程:双曲线的标准方程:抛物线的标准方程:知识回顾(四)知识回顾(五) 椭
圆抛
物
线双
曲
线知识回顾(五)yxoyxoyxo知识回顾(六)知识回顾(六)0
P(3,2),长轴长是短轴长的3倍,求该椭圆的方程。 解:由题知,椭圆的方程为标准方程。 小结:本题用待定系数法求椭圆的标准方程,
但在无法判断焦点所在的坐标轴时,要分情况讨论 解: 依题意,双曲线焦点在y轴上,半焦距c=10,典型例题典型例题2【例2】 已知双曲线的中心在坐标原点,一个焦点为F(0,10),两条渐近线的方程为 ,求该双曲线的标准方程.小结:本题是利用渐近线方程、a,b,c三者之间的
关系,求解双曲线方程可设标准方程为为 ,故双曲线方程为又渐近线方程故典型例题【例3】已知抛物线C的顶点在原点,焦点F在x轴的正半轴上,
设A、B是抛物线C上的两个动点(AB不垂直于x轴),
且AF+BF=8,线段AB的垂直平分线恒经过点Q(6、0),求此抛物线方程。 典型例题3典型例题典型例题3【例3】已知抛物线C的顶点在原点,焦点F在x轴的正半轴上,
设A、B是抛物线C上的两个动点(AB不垂直于x轴),
且AF+BF=8,线段AB的垂直平分线恒经过点Q(6、0),求此抛物线方程。 小结:抛物线的标准方程有四种形式,用待定系数法求解是最基本的方法。
本题是综合抛物线的定义及中垂线的有关知识解题。 解:典型例题典型例题4【例4】 (2009·江苏)如图所示,在平面直角坐标系xOy中,A1,A2,B1,B2为椭圆 (a>b>0)的四个顶点,F为其右焦点,直线A1B2与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,求该椭圆的离心率.
解 由题意结合图形得,
即-bx+ay=ab, ①
即bx-cy=bc, ② 由①②求得:典型例题典型例题4【例4】 (2009·江苏)如图所示,在平面直角坐标系xOy中,A1,A2,B1,B2为椭圆 (a>b>0)的四个顶点,F为其右焦点,直线A1B2与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,求该椭圆的离心率.
解:
(续)即4c2+a2+2ac+c2=4a2-8ac+4c2,
c2+10ac-3a2=0,∴e2+10e-3=0.
又∵0
体现了方程的思想。 变式训练变式训练 已知双曲线 (a>0,b>0)的左、右焦点分别为F1、
F2,点P在右支上,|PF1|=4|PF2|,求双曲线离心率e的最大值.解 方法一 在△PF1F2中,cos∠F1PF2= ,要求e的最大值,只须求cos∠F1PF2的最小值,
当cos∠F1PF2=-1时e最大值为 .变式训练变式训练 已知双曲线 (a>0,b>0)的左、右焦点分别为F1、
F2,点P在右支上,|PF1|=4|PF2|,求双曲线离心率e的最大值.
方法二 由以上可知小结:本题考查了双曲线的两种定义形式,熟练运用
定义解题是基本思路。 课堂小结 本节课主要复习圆锥曲线的定义、标准方程、
几何性质及应用,同时注重与其他知识的综合
运用,在解题时除了要熟练掌握圆锥曲线基本知
识外,需注重利用数形结合思想解决实际问题。
课堂小结
