苏教版高中数学选修2-1课件:2.4.2 抛物线的简单几何性质 共27张PPT
文档属性
| 名称 | 苏教版高中数学选修2-1课件:2.4.2 抛物线的简单几何性质 共27张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-16 22:54:39 | ||
图片预览




文档简介
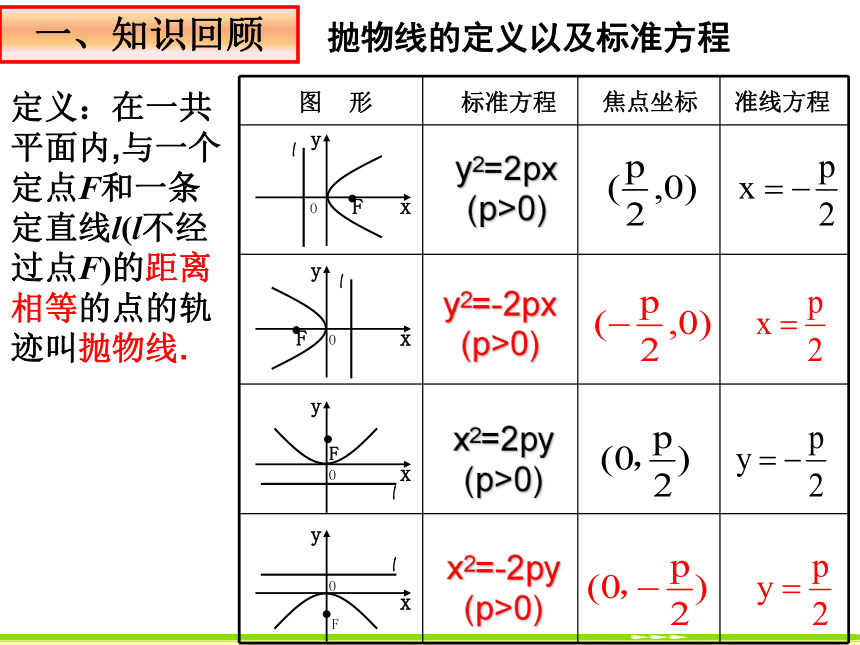
课件27张PPT。§2.4.2 抛物线的简单几何性质定义:在一共平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.抛物线的定义以及标准方程y2=-2px
(p>0)x2=2py
(p>0)y2=2px
(p>0)x2=-2py
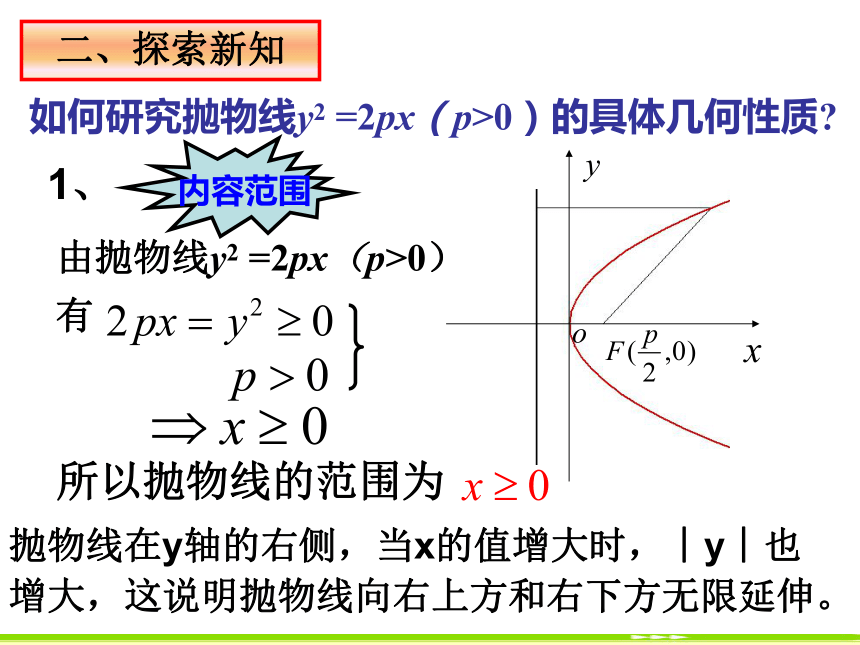
(p>0)一、知识回顾由抛物线y2 =2px(p>0)所以抛物线的范围为二、探索新知如何研究抛物线y2 =2px(p>0)的具体几何性质?抛物线在y轴的右侧,当x的值增大时,︱y︱也增大,这说明抛物线向右上方和右下方无限延伸。即点(x,-y) 也在抛物线上,故 抛物线y2 = 2px(p>0)关于x轴对称.则 (-y)2 = 2px若点(x,y)在抛物线上, 即满足y2 = 2px, 定义:抛物线与它的轴的交点叫做抛物线的顶点。y2 = 2px (p>0)中,
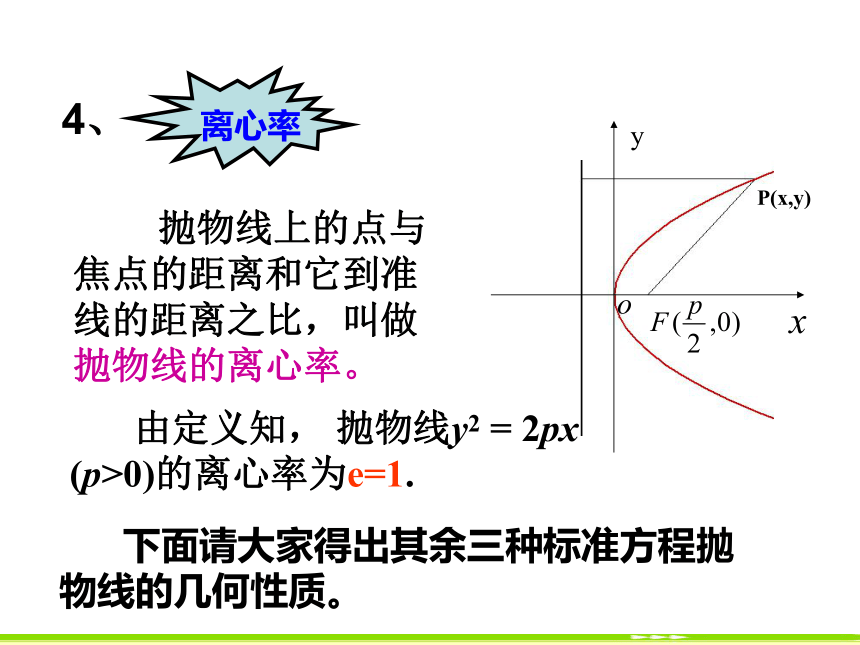
令y=0,则x=0.即:抛物线y2 = 2px (p>0)的顶点(0,0).注:这与椭圆有四个顶点,双曲线有两个顶点不同。 抛物线上的点与焦点的距离和它到准线的距离之比,叫做抛物线的离心率。 由定义知, 抛物线y2 = 2px (p>0)的离心率为e=1. 下面请大家得出其余三种标准方程抛物线的几何性质。(二)归纳:抛物线的几何性质y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)x≥0
y∈Rx≤0
y∈Ry≥0
x∈Ry ≤ 0
x∈R(0,0)x轴y轴1特点:1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;2.抛物线只有一条对称轴,没有
对称中心;3.抛物线只有一个顶点、
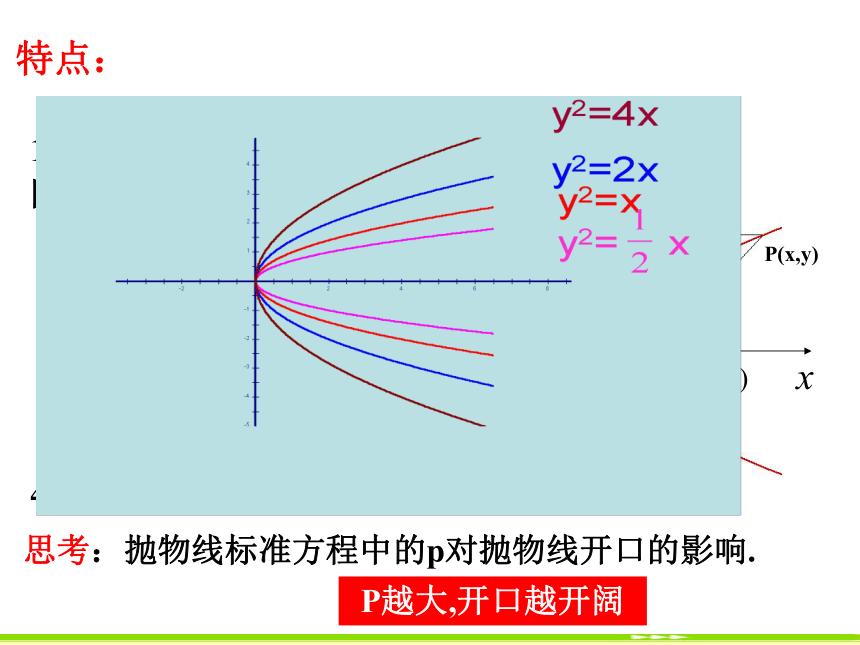
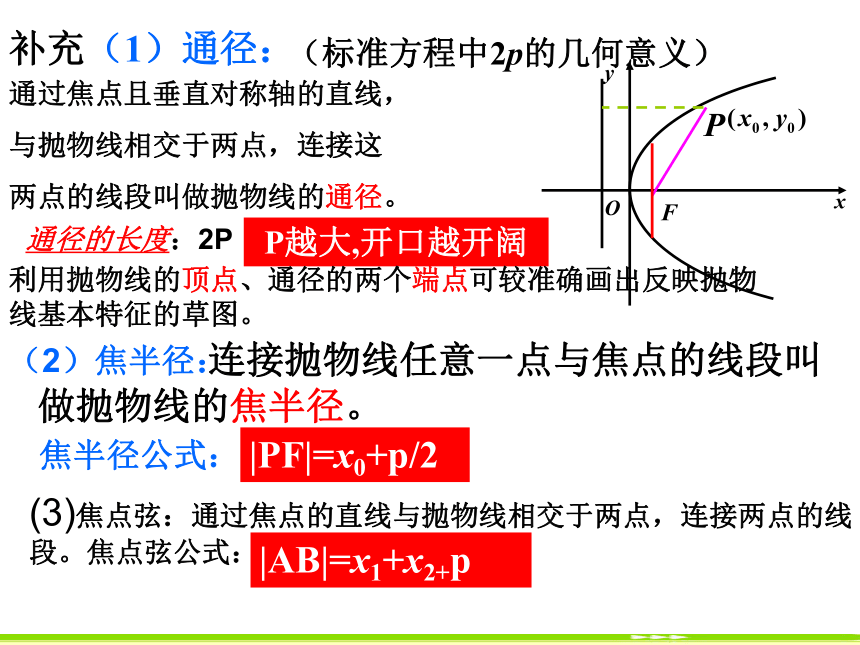
一个焦点、一条准线;4.抛物线的离心率是确定的,为1;思考:抛物线标准方程中的p对抛物线开口的影响.P越大,开口越开阔补充(1)通径:通过焦点且垂直对称轴的直线,
与抛物线相交于两点,连接这
两点的线段叫做抛物线的通径。|PF|=x0+p/2FP通径的长度:2PP越大,开口越开阔(2)焦半径: 连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。焦半径公式:(标准方程中2p的几何意义)利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图。(3)焦点弦:通过焦点的直线与抛物线相交于两点,连接两点的线段。焦点弦公式:F|=|AB|=x1+x2+py2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0) 因为抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),解:所以设方程为:因此所求抛物线标准方程为:三、典例精析坐标轴当焦点在x(y)轴上,开口方向不定时,设为y2=2mx(m ≠0)
(x2=2my (m≠0)),可避免讨论 例1:已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),求它的标准方程.练习:1、已知抛物线的顶点在原点,对称轴为x轴,焦点在直线3x-4y-12=0上,那么抛物线通径长是 .2、已知点A(-2,3)与抛物线
的焦点的距离是5,则P= 。 4例2、斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长。1.已知M为抛物线 上一动点,F为抛物线的焦点,
定点P(3,1),则 的最小值为( )
(A)3 (B)4 (C)5 (D)6 B.分析:直线与抛物线有一个公共点的情况有两种情形:一种是直线平行于抛物线的对称轴;
另一种是直线与抛物线相切. 判断直线与抛物线位置关系的操作程序把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线的
对称轴平行相交(一个交点) 计 算 判 别 式分析:
直线与抛物线有两个公共点时△>0 分析:
直线与抛物线没有公共点时△<0 注:在方程中,二次项系数含有k,所以要对k进行讨论
作图要点:画出直线与抛物线只有一个公共点时的情形,观察直线绕点P转动的情形
(p>0)x2=2py
(p>0)y2=2px
(p>0)x2=-2py
(p>0)一、知识回顾由抛物线y2 =2px(p>0)所以抛物线的范围为二、探索新知如何研究抛物线y2 =2px(p>0)的具体几何性质?抛物线在y轴的右侧,当x的值增大时,︱y︱也增大,这说明抛物线向右上方和右下方无限延伸。即点(x,-y) 也在抛物线上,故 抛物线y2 = 2px(p>0)关于x轴对称.则 (-y)2 = 2px若点(x,y)在抛物线上, 即满足y2 = 2px, 定义:抛物线与它的轴的交点叫做抛物线的顶点。y2 = 2px (p>0)中,
令y=0,则x=0.即:抛物线y2 = 2px (p>0)的顶点(0,0).注:这与椭圆有四个顶点,双曲线有两个顶点不同。 抛物线上的点与焦点的距离和它到准线的距离之比,叫做抛物线的离心率。 由定义知, 抛物线y2 = 2px (p>0)的离心率为e=1. 下面请大家得出其余三种标准方程抛物线的几何性质。(二)归纳:抛物线的几何性质y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)x≥0
y∈Rx≤0
y∈Ry≥0
x∈Ry ≤ 0
x∈R(0,0)x轴y轴1特点:1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;2.抛物线只有一条对称轴,没有
对称中心;3.抛物线只有一个顶点、
一个焦点、一条准线;4.抛物线的离心率是确定的,为1;思考:抛物线标准方程中的p对抛物线开口的影响.P越大,开口越开阔补充(1)通径:通过焦点且垂直对称轴的直线,
与抛物线相交于两点,连接这
两点的线段叫做抛物线的通径。|PF|=x0+p/2FP通径的长度:2PP越大,开口越开阔(2)焦半径: 连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。焦半径公式:(标准方程中2p的几何意义)利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图。(3)焦点弦:通过焦点的直线与抛物线相交于两点,连接两点的线段。焦点弦公式:F|=|AB|=x1+x2+py2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0) 因为抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),解:所以设方程为:因此所求抛物线标准方程为:三、典例精析坐标轴当焦点在x(y)轴上,开口方向不定时,设为y2=2mx(m ≠0)
(x2=2my (m≠0)),可避免讨论 例1:已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),求它的标准方程.练习:1、已知抛物线的顶点在原点,对称轴为x轴,焦点在直线3x-4y-12=0上,那么抛物线通径长是 .2、已知点A(-2,3)与抛物线
的焦点的距离是5,则P= 。 4例2、斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长。1.已知M为抛物线 上一动点,F为抛物线的焦点,
定点P(3,1),则 的最小值为( )
(A)3 (B)4 (C)5 (D)6 B.分析:直线与抛物线有一个公共点的情况有两种情形:一种是直线平行于抛物线的对称轴;
另一种是直线与抛物线相切. 判断直线与抛物线位置关系的操作程序把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线的
对称轴平行相交(一个交点) 计 算 判 别 式分析:
直线与抛物线有两个公共点时△>0 分析:
直线与抛物线没有公共点时△<0 注:在方程中,二次项系数含有k,所以要对k进行讨论
作图要点:画出直线与抛物线只有一个公共点时的情形,观察直线绕点P转动的情形
