苏教版高中数学选修2-1课件:2.2.1 椭圆及其标准方程 共37张PPT
文档属性
| 名称 | 苏教版高中数学选修2-1课件:2.2.1 椭圆及其标准方程 共37张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 754.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-16 22:58:02 | ||
图片预览










文档简介
课件37张PPT。2.1.1椭圆及其标准方程如何来精确地设计、制作以及建造出现实生活中这些椭圆形的具体物件呢?生活中存在的椭圆一.课题导入:椭圆的画法椭圆及其标准方程F1F2一、椭圆的定义: 平面内与两个定点F1、F2的距离间的和等于常数(大于|F1F2|)的点的轨迹被叫做椭圆,这两个定点被叫做椭圆的焦点,两焦点的距离被叫做椭圆的焦距.问题1:当常数等于|F1F2|时,点M的轨迹
是什么?
问题2:当常数小于|F1F2|时,点M的轨迹
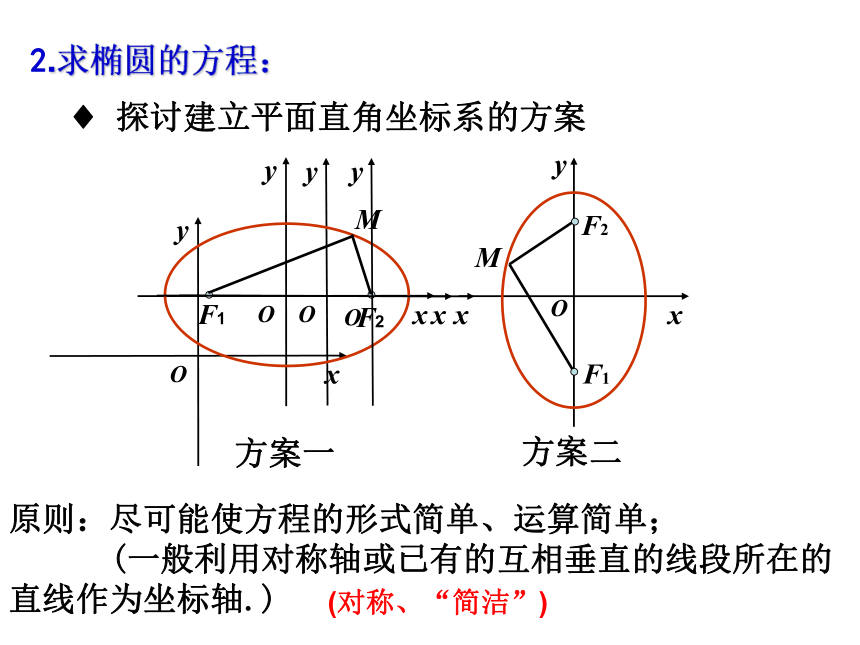
是什么?线段F1F2轨迹不存在1、椭圆的定义: 平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。几点说明:1、F1、F2是两个不同的定点;2、M是椭圆上任意一点,且|MF1| + |MF2| = 常数;3、通常这个常数记为2a,焦距记为2c,且2a>2c(?);4、如果2a = 2c,则M点的轨迹是线段F1F2.5、如果2a < 2c,则M点的轨迹不存在.(由三角形的性质知) 下面我们来求椭圆的标准方程.? 探讨建立平面直角坐标系的方案方案一2.求椭圆的方程:原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)(对称、“简洁”)OXYF1F2M如图所示: F1、F2为两定点,且|F1F2|=2c,求平面内到两定点F1、F2距离之和为定值2a(2a>2c)的动点M的轨迹方程。 解:以F1F2所在直线为X轴, F1F2 的中点为原点建立平面直角坐标系,则焦点F1、F2的坐标分别为(-c,0)、 (c,0)。(-c,0)(c,0)(x,y) 设M(x,y)为所求轨迹上的任意一点,则:|MF1|+ |MF2|=2aOXYF1F2M(-c,0)(c,0)(x,y)两边平方得:a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2即:(a2-c2)x2+a2y2=a2(a2-c2)因为2a>2c,即a>c,所以a2-c2>0,令a2-c2=b2,其中b>0,代入上式可得:b2x2+a2y2=a2b2两边同时除以a2b2得:(a>b>0)这个方程叫做椭圆的标准方程,
它所表示的椭圆的焦点在x 轴上。aA1yOF1F2xB2B1A2cb三、①椭圆方程的几何意义:如果椭圆的焦点在y轴上,
焦点是F1(o,-c)、F2(0,c)方程是怎样呢?②椭圆的第二种形式: 图 形方 程焦 点F(±c,0)在X轴上F(0,±c)在Y轴上a,b,c之间的关系c2=a2-b2P={M||MF1|+|MF2|=2a} (2a>2c>0)定 义四、两类标准方程的对照表:注:哪个分母大,焦点就在相应的哪条坐标轴上!Y椭圆的标准方程的再认识:(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1(3)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。(4)由椭圆的标准方程可以求出三个参数a、b、c的值。(2)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪
一个轴上。例1 写出适合下列条件的椭圆的标准方程 (1) a =4,b=1,焦点在 x 轴上;
(2) a =4,b=1,焦点在坐标轴上;
或五、数学应用:例2、求满足下列条件的椭圆的标准方程:(1)两焦点的坐标分别是(-4,0)、(4,0),
椭圆上一点P到两焦点距离之和等于10。(2)两焦点的坐标分别是(-2,0)、(2,0),
且椭圆经过点P 。(1)两焦点的坐标分别是(-4,0)、(4,0),椭圆上一点P到两焦点距离之和等于10。解:因为椭圆的焦点在X轴上,所以可设它的方程
为:?2a=10,2c=8即 a=5,c=4故 b2=a2-c2=52-42=9所以椭圆的标准方程为:(2)两焦点的坐标分别是(-2,0)、(2,0),且
椭圆经过点P 。解:因为椭圆的焦点在X轴上,所以可设它的方程为:?由椭圆的定义可知:又因 c=2,所以椭圆的标准方程为:故 b2=a2-c2=10-22=6课堂练习2:1.口答:下列方程哪些表示椭圆? 若是,则判定其焦点在何轴?
并指明 ,写出焦点坐标.?1、方程 ,分别求方程满足下列条件
的m的取值范围:
①表示一个圆;
探究与互动:析:方程表示圆需要满足的条件:1、方程 ,分别求方程满足下列条件
的m的取值范围:
①表示一个圆;
②表示一个椭圆;
探究与互动:析:方程表示一个椭圆需要满足的条件:1、方程 ,分别求方程满足下列条件
的m的取值范围:
①表示一个圆;
②表示一个椭圆;
探究与互动:析:方程表示一个椭圆需要满足的条件:1、方程 ,分别求方程满足下列条件
的m的取值范围:
①表示一个圆;
②表示一个椭圆;
③表示焦点在x轴上的椭圆。探究与互动:析:表示焦点在x轴上的椭圆需要满足的条件:解题感悟:
方程表示椭圆时要看清楚限制条件,焦点在哪个轴上。练习3:若方程4x2+ky2=1表示的曲线是焦点在y轴上的椭圆,求k的取值范围。∵方程表示的曲线是焦点在y轴上的椭圆解之得:0∴|AB|+|AC|=12>|BC|,
∴点A的轨迹是以B?C为焦点的椭圆(除去与x轴的交点).
且2a=12,2c=8,及a2=b2+c2得a2=36,b2=20.
故点A的轨迹方程是 (y≠0).例4:已知△ABC的一边BC长为8,周长为20,求顶点A的轨迹方程.解:以BC边所在直线为x轴,BC中点为原点,建立如右图所示的直角坐标系,则B?C两点的坐标分别为(-4,0)?(4,0).定义法练习:已知A(-1,0),B(1,0),线段CA、AB、CB的长成等差数列,则点C的轨迹方程是_____________.x2/4+y2/3=1椭圆及其标准方程(2)分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹复习旧知例1求焦点在坐标轴上,且经过两点
的椭圆的标准方程。x2/15+y2/5=1分析一:当焦点在x轴上时,
设方程x2/a2+y2/b2=1 当焦点在x轴上时,
设方程x2/b2+y2/a2=1分析二:设方程mx2+ny2=1(m>0,n>0)(2)求与椭圆x2/5+y2/4=1有公共焦点,且过点(3,0)的椭圆的标准方程。
x2/9+y2/8=1
(3)已知椭圆x2+2y2=a2(a>0)的左焦点到直线l:x-y-2=0的距离为 ,求椭圆方程。
x2/8+y2/4=1 例2、在圆 上任取一点P,过点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?相关点法(转移法):即利用中间变量求曲线方程.PABMxyo练习:课本P42,练习第4题七.走进高考: (海南2009高考(理)第20题第一问)
已知椭圆的中心为直角坐标系xOy的原点,焦点在X轴上,它的一个顶点到两个焦点的距离分别是7和1. 求椭圆的方程.
(海南2008高考(文)第15题)
过椭圆 的右焦点作一条斜率为1的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________.
是什么?
问题2:当常数小于|F1F2|时,点M的轨迹
是什么?线段F1F2轨迹不存在1、椭圆的定义: 平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。几点说明:1、F1、F2是两个不同的定点;2、M是椭圆上任意一点,且|MF1| + |MF2| = 常数;3、通常这个常数记为2a,焦距记为2c,且2a>2c(?);4、如果2a = 2c,则M点的轨迹是线段F1F2.5、如果2a < 2c,则M点的轨迹不存在.(由三角形的性质知) 下面我们来求椭圆的标准方程.? 探讨建立平面直角坐标系的方案方案一2.求椭圆的方程:原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)(对称、“简洁”)OXYF1F2M如图所示: F1、F2为两定点,且|F1F2|=2c,求平面内到两定点F1、F2距离之和为定值2a(2a>2c)的动点M的轨迹方程。 解:以F1F2所在直线为X轴, F1F2 的中点为原点建立平面直角坐标系,则焦点F1、F2的坐标分别为(-c,0)、 (c,0)。(-c,0)(c,0)(x,y) 设M(x,y)为所求轨迹上的任意一点,则:|MF1|+ |MF2|=2aOXYF1F2M(-c,0)(c,0)(x,y)两边平方得:a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2即:(a2-c2)x2+a2y2=a2(a2-c2)因为2a>2c,即a>c,所以a2-c2>0,令a2-c2=b2,其中b>0,代入上式可得:b2x2+a2y2=a2b2两边同时除以a2b2得:(a>b>0)这个方程叫做椭圆的标准方程,
它所表示的椭圆的焦点在x 轴上。aA1yOF1F2xB2B1A2cb三、①椭圆方程的几何意义:如果椭圆的焦点在y轴上,
焦点是F1(o,-c)、F2(0,c)方程是怎样呢?②椭圆的第二种形式: 图 形方 程焦 点F(±c,0)在X轴上F(0,±c)在Y轴上a,b,c之间的关系c2=a2-b2P={M||MF1|+|MF2|=2a} (2a>2c>0)定 义四、两类标准方程的对照表:注:哪个分母大,焦点就在相应的哪条坐标轴上!Y椭圆的标准方程的再认识:(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1(3)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。(4)由椭圆的标准方程可以求出三个参数a、b、c的值。(2)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪
一个轴上。例1 写出适合下列条件的椭圆的标准方程 (1) a =4,b=1,焦点在 x 轴上;
(2) a =4,b=1,焦点在坐标轴上;
或五、数学应用:例2、求满足下列条件的椭圆的标准方程:(1)两焦点的坐标分别是(-4,0)、(4,0),
椭圆上一点P到两焦点距离之和等于10。(2)两焦点的坐标分别是(-2,0)、(2,0),
且椭圆经过点P 。(1)两焦点的坐标分别是(-4,0)、(4,0),椭圆上一点P到两焦点距离之和等于10。解:因为椭圆的焦点在X轴上,所以可设它的方程
为:?2a=10,2c=8即 a=5,c=4故 b2=a2-c2=52-42=9所以椭圆的标准方程为:(2)两焦点的坐标分别是(-2,0)、(2,0),且
椭圆经过点P 。解:因为椭圆的焦点在X轴上,所以可设它的方程为:?由椭圆的定义可知:又因 c=2,所以椭圆的标准方程为:故 b2=a2-c2=10-22=6课堂练习2:1.口答:下列方程哪些表示椭圆? 若是,则判定其焦点在何轴?
并指明 ,写出焦点坐标.?1、方程 ,分别求方程满足下列条件
的m的取值范围:
①表示一个圆;
探究与互动:析:方程表示圆需要满足的条件:1、方程 ,分别求方程满足下列条件
的m的取值范围:
①表示一个圆;
②表示一个椭圆;
探究与互动:析:方程表示一个椭圆需要满足的条件:1、方程 ,分别求方程满足下列条件
的m的取值范围:
①表示一个圆;
②表示一个椭圆;
探究与互动:析:方程表示一个椭圆需要满足的条件:1、方程 ,分别求方程满足下列条件
的m的取值范围:
①表示一个圆;
②表示一个椭圆;
③表示焦点在x轴上的椭圆。探究与互动:析:表示焦点在x轴上的椭圆需要满足的条件:解题感悟:
方程表示椭圆时要看清楚限制条件,焦点在哪个轴上。练习3:若方程4x2+ky2=1表示的曲线是焦点在y轴上的椭圆,求k的取值范围。∵方程表示的曲线是焦点在y轴上的椭圆解之得:0
∴点A的轨迹是以B?C为焦点的椭圆(除去与x轴的交点).
且2a=12,2c=8,及a2=b2+c2得a2=36,b2=20.
故点A的轨迹方程是 (y≠0).例4:已知△ABC的一边BC长为8,周长为20,求顶点A的轨迹方程.解:以BC边所在直线为x轴,BC中点为原点,建立如右图所示的直角坐标系,则B?C两点的坐标分别为(-4,0)?(4,0).定义法练习:已知A(-1,0),B(1,0),线段CA、AB、CB的长成等差数列,则点C的轨迹方程是_____________.x2/4+y2/3=1椭圆及其标准方程(2)分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹复习旧知例1求焦点在坐标轴上,且经过两点
的椭圆的标准方程。x2/15+y2/5=1分析一:当焦点在x轴上时,
设方程x2/a2+y2/b2=1 当焦点在x轴上时,
设方程x2/b2+y2/a2=1分析二:设方程mx2+ny2=1(m>0,n>0)(2)求与椭圆x2/5+y2/4=1有公共焦点,且过点(3,0)的椭圆的标准方程。
x2/9+y2/8=1
(3)已知椭圆x2+2y2=a2(a>0)的左焦点到直线l:x-y-2=0的距离为 ,求椭圆方程。
x2/8+y2/4=1 例2、在圆 上任取一点P,过点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?相关点法(转移法):即利用中间变量求曲线方程.PABMxyo练习:课本P42,练习第4题七.走进高考: (海南2009高考(理)第20题第一问)
已知椭圆的中心为直角坐标系xOy的原点,焦点在X轴上,它的一个顶点到两个焦点的距离分别是7和1. 求椭圆的方程.
(海南2008高考(文)第15题)
过椭圆 的右焦点作一条斜率为1的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________.
