2018-2019学年湖南省长沙市岳麓区麓山国际实验学校七年级(下)开学数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年湖南省长沙市岳麓区麓山国际实验学校七年级(下)开学数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 219.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-17 10:33:03 | ||
图片预览


文档简介
2018-2019学年湖南省长沙市岳麓区麓山国际实验学校七年级(下)开学数学试卷
一、选择题(每小题3分,共36分)
1.(3分)﹣2019的相反数是( )
A.﹣2019 B.2019 C.﹣ D.
2.(3分)下列说法中错误的是( )
A.﹣x2y的系数是﹣ B.0是单项式
C.﹣x是一次单项式 D.xy2的次数是2
3.(3分)已知∠A=70°,则∠A的余角等于( )
A.70° B.20° C.110° D.10°
4.(3分)计算3a3﹣a3的结果是( )
A.2 B.2a C.2a3 D.3a3
5.(3分)中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图①表示的是(+2)+(﹣2),根据刘徵的这种表示法,可推算图②中所表示的算式为( )
A.(+3)+(+6) B.(﹣3)+(﹣6) C.(﹣3)+(+6) D.(+3)+(﹣6)
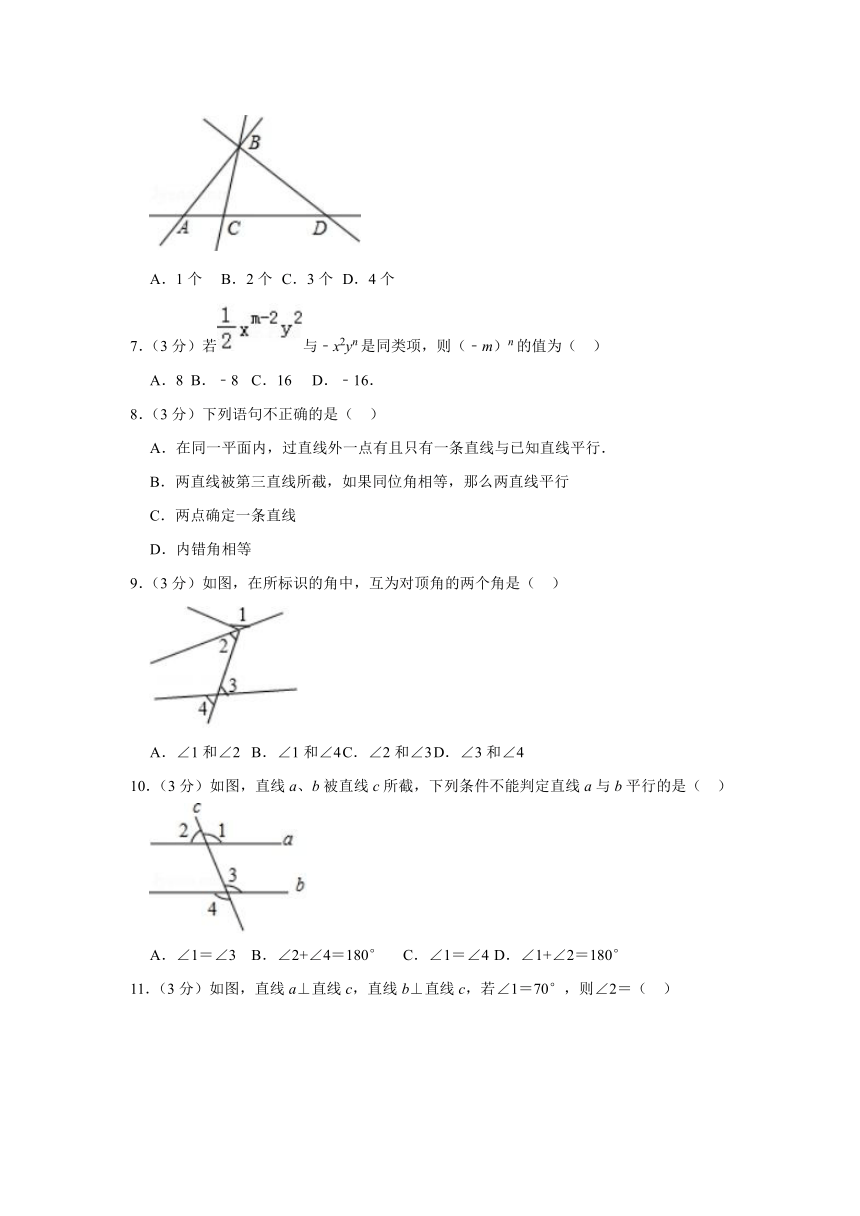
6.(3分)观察图形,下列说法正确的个数是( )
(1)直线BA和直线AB是同一条直线;
(2)AB+BD>AD;
(3)射线AC和射线AD是同一条射线;
(4)三条直线两两相交时,一定有三个交点.
A.1个 B.2个 C.3个 D.4个
7.(3分)若与﹣x2yn是同类项,则(﹣m)n的值为( )
A.8 B.﹣8 C.16 D.﹣16.
8.(3分)下列语句不正确的是( )
A.在同一平面内,过直线外一点有且只有一条直线与已知直线平行.
B.两直线被第三直线所截,如果同位角相等,那么两直线平行
C.两点确定一条直线
D.内错角相等
9.(3分)如图,在所标识的角中,互为对顶角的两个角是( )
A.∠1和∠2 B.∠1和∠4 C.∠2和∠3 D.∠3和∠4
10.(3分)如图,直线a、b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠1+∠2=180°
11.(3分)如图,直线a⊥直线c,直线b⊥直线c,若∠1=70°,则∠2=( )
A.70° B.90° C.110° D.80°
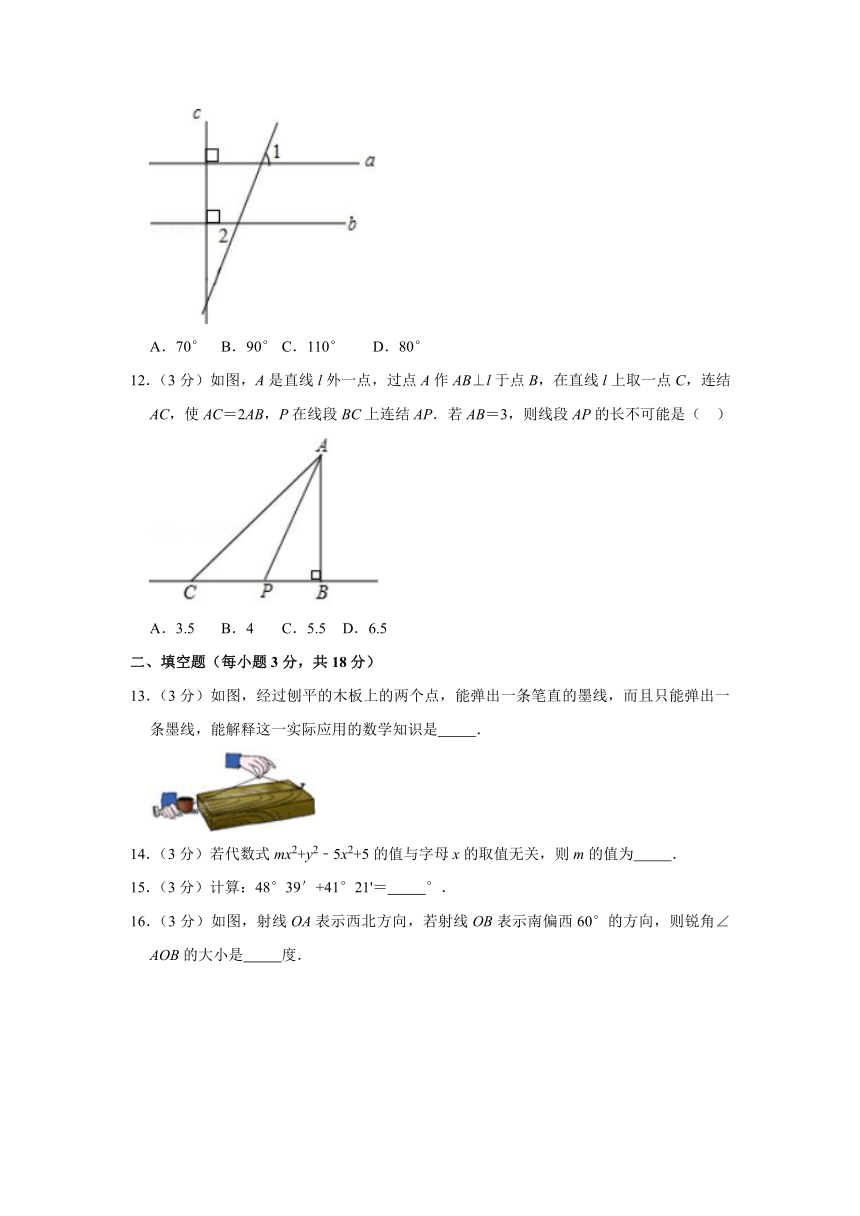
12.(3分)如图,A是直线l外一点,过点A作AB⊥l于点B,在直线l上取一点C,连结AC,使AC=2AB,P在线段BC上连结AP.若AB=3,则线段AP的长不可能是( )
A.3.5 B.4 C.5.5 D.6.5
二、填空题(每小题3分,共18分)
13.(3分)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 .
14.(3分)若代数式mx2+y2﹣5x2+5的值与字母x的取值无关,则m的值为 .
15.(3分)计算:48°39′+41°21'= °.
16.(3分)如图,射线OA表示西北方向,若射线OB表示南偏西60°的方向,则锐角∠AOB的大小是 度.
17.(3分)互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利20元,则这件商品的进价为 元.
18.(3分)已知线段AB=8cm,点C是线段AB所在直线上一点.下列说法:①若点C为线段AB的中点,则AC=4cm;②若AC=4cm,则点C为线段AB的中点;③AC>BC,则点C一定在线段AB的延长线上;④线段AC与BC的长度和一定不小于8cm,其中正确的有 (填写正确答案的序号).
三、解答题(共66分)
19.(8分)解方程:
(1)4x+3(2x﹣3)=12﹣(x﹣1)
(2)y﹣=2﹣
20.(6分)先化简,再求值:(4a2﹣2ab+b2)﹣3(a2﹣ab+b2),其中a=﹣1,b=﹣.
21.(6分)如图①,长方体的上下底面是边长为1的正方形,高为2;如图②,在5×5的正方形网格中,每个小方格都是边长为1的正方形.
(1)在图②中画出这个长方体的一个展开图;
(2)如果一只蚂蚁从顶点A处沿长方体表面爬行到顶点B处,请你在(1)中所画的展开图中画出该蚂蚁爬行的最短路线,并说明理由.
22.(6分)如果x=1是方程的解,
(1)求m的值;
(2)求关于y的方程m(y﹣3)﹣2=m(2y﹣5)的解.
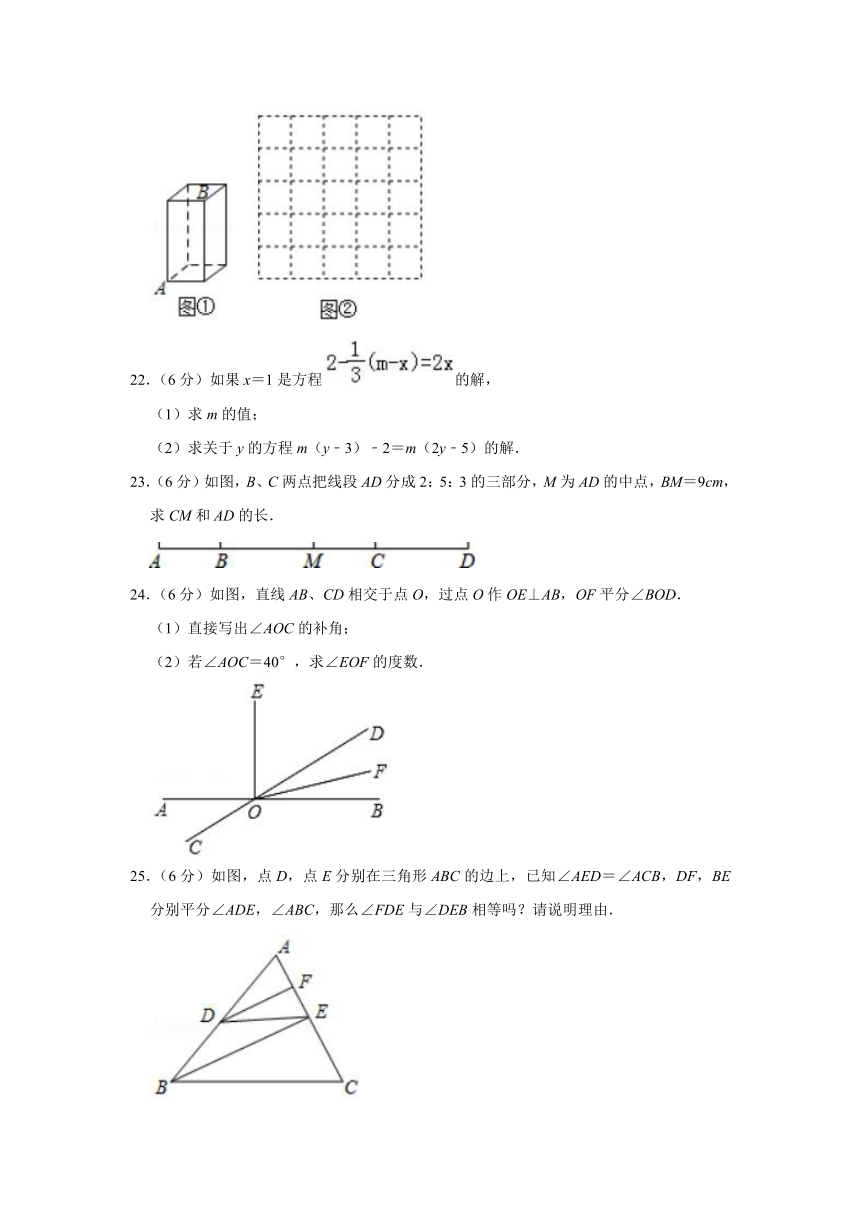
23.(6分)如图,B、C两点把线段AD分成2:5:3的三部分,M为AD的中点,BM=9cm,求CM和AD的长.
24.(6分)如图,直线AB、CD相交于点O,过点O作OE⊥AB,OF平分∠BOD.
(1)直接写出∠AOC的补角;
(2)若∠AOC=40°,求∠EOF的度数.
25.(6分)如图,点D,点E分别在三角形ABC的边上,已知∠AED=∠ACB,DF,BE分别平分∠ADE,∠ABC,那么∠FDE与∠DEB相等吗?请说明理由.
26.(6分)某人原计划用26天生产一批零件,工作两天后因改变了操作方法,每天比原来多生产5个零件结果提前4天完成任务,问原来每天生产多少个零件?这批零件有多少个?
27.(8分)如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连接EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD∥BC和AB∥CD.
请完成下面的推理过程,并填空:
∵∠1=∠2( )
∠1=∠AGH( )
∴∠2=∠AGH( )
∴AD∥BC( )
∴∠ADE=∠C( )
∵∠A=∠C( )
∴∠ADE=∠A( )
∴AB∥CD( ).
28.(8分)如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
2018-2019学年湖南省长沙市岳麓区麓山国际实验学校七年级(下)开学数学试卷
参考答案与试题解析
一、选择题(每小题3分,共36分)
1.【解答】解:﹣2019的相反数是:2019.
故选:B.
2.【解答】解:该单项式是次数为3,故D错误;
故选:D.
3.【解答】解:∠A的余角:90°﹣70°=20°,
故选:B.
4.【解答】解:3a3﹣a3=2a3,
故选:C.
5.【解答】解:根据题意知,图②表示的数值为(+3)+(﹣6)=﹣3.
故选:D.
6.【解答】解:(1)直线BA和直线AB是同一条直线;正确,
(2)AB+BD>AD;正确
(3)射线AC和射线AD是同一条射线;正确,
(4)三条直线两两相交时,一定有三个交点,还可能有一个,故不正确.
共3个说法正确.
故选:C.
7.【解答】解:与﹣x2yn是同类项,
∴m﹣2=2,n=2,解得:m=4,n=2.
(﹣m)n=(﹣4)2=16.
故选:C.
8.【解答】解:A、在同一平面内,过直线外一点有且只有一条直线与已知直线平行,故A正确;
B、两直线被第三直线所截,如果同位角相等,那么两直线平行,故B正确;
C、两点确定一条直线,故C正确;
D、两直线平行,内错角相等,故D错误;
故选:D.
9.【解答】解:观察图形可知,互为对顶角的两个角是∠3和∠4.
故选:D.
10.【解答】解:由∠1=∠3,可得直线a与b平行,故A能判定;
由∠2+∠4=180°,∠2=∠5,∠4=∠3,可得∠3+∠5=180°,故直线a与b平行,故B能判定;
由∠1=∠4,∠4=∠3,可得∠1=∠3,故直线a与b平行,故C能判定;
由∠1+∠2=180°,不能判定直线a与b平行.
故选:D.
11.【解答】解:∵直线a⊥直线c,直线b⊥直线c,
∴a∥b,
∴∠1=∠3,
∵∠3=∠2,
∴∠2=∠1=70°.
故选:A.
12.【解答】解:∵过点A作AB⊥l于点B,AC=2AB,P在线段BC上连结AP,AB=3,
∴AC=6,
∴3≤AP≤6,
故AP不可能是6.5,
故选:D.
二、填空题(每小题3分,共18分)
13.【解答】解:能解释这一实际应用的数学知识是:两点确定一条直线,
故答案为:两点确定一条直线.
14.【解答】解:∵代数式mx2+y2﹣5x2+5的值与字母x的取值无关,
∴m﹣5=0,
解得:m=5.
故答案为:5.
15.【解答】解:原式=89°60′=90°,
故答案为:90.
16.【解答】解:由图可知:∠AOB=180°﹣45°﹣60°=75°.
故答案为:75.
17.【解答】解:设该商品的进价为x元,
根据题意得:200×0.5﹣x=20,
解得:x=80.
故答案为:80.
18.【解答】解:∵线段AB=8cm,点C是线段AB所在直线上一点,
∴①若点C为线段AB的中点,则AC=4cm是正确的;
②若AC=4cm,则点C为线段AB的中点或在线段AB的反向延长线上,原来的说法是错误的;
③AC>BC,则点C可能在线段AB上,原来的说法是错误的;
④线段AC与BC的长度和一定不小于8cm是正确的.
故答案为:①④.
三、解答题(共66分)
19.【解答】解:(1)去括号得:4x+6x﹣9=12﹣x+1,
移项,得:4x+6x+x=12+1+9,
合并同类项,得:11x=2,
系数化为1,得:x=2;
(2)去分母,得:10y﹣2(y+2)=10﹣5(y﹣3),
去括号,得:10y﹣2y﹣4=20﹣5y+15,
移项,得:10y﹣2y+5y=20+15+4,
合并同类项,得:13y=39,
系数化为1,得:y=3.
20.【解答】解:原式=4a2﹣2ab+b2﹣3a2+3ab﹣3b2
=a2+ab﹣2b2,
当a=﹣1,b=时,
原式=1+﹣
=1.
21.【解答】解:(1)其展开图如下图所示:
(2)如图所示,蚂蚁爬行的最短路线即为线段AB,
理由是:两点之间线段最短.
22.【解答】解:(1)将x=1代入方程得:2﹣(m﹣1)=2,
去分母得6﹣m+1=6,即m=1;
(2)将m=1代入方程得y﹣3﹣2=2y﹣5,
移项合并得:y=0.
23.【解答】解:设AB=2x(cm),BC=5x(cm),CD=3x(cm)
则AD=AB+BC+CD=10x(cm),
∵M是AD的中点
∴AM=MD=AD=5xcm
∴BM=AM﹣AB=5x﹣2x=3xcm
∵BM=9cm,
∴3x=9,
解得:x=3,
故CM=MD﹣CD=5x﹣3x=2x=2×3=6cm,
AD=10x=10×3=30(cm).
24.【解答】解:(1)∠AOC的补角是∠AOD,∠BOC;
(2)∵∠AOC=40°,
∴∠BOD=∠AOC=40°,
∵OF平分∠BOD,
∴∠BOF=20°,
∵OE⊥AB,
∴∠EOB=90°,
∴∠EOF=90°﹣20°=70°.
25.【解答】解:∠FDE=∠DEB,
理由:∵∠AED=∠ACB,
∴DE∥BC,
∴∠ADE=∠ABC,
∵DF,BE分别平分∠ADE,∠ABC,
∴∠ADF=∠ADE,∠ABE=∠ABC,
∴∠ADF=∠ABE,
∴DF∥BE,
∴∠FDE=∠DEB.
26.【解答】解:设原来每天生产x个零件,根据题意可得:
26x=2x+(x+5)×20,
解得:x=25,
故26×25=650(个).
答:原来每天生产25个零件,这批零件有650个.
27.【解答】证明:∵∠1=∠2(已知)
∠1=∠AGH(对顶角相等)
∴∠2=∠AGH(等量代换)
∴AD∥BC(同位角相等,两直线平行)
∴∠ADE=∠C(两直线平行,同位角相等)
∵∠A=∠C(已知)
∴∠ADE=∠A(等量代换)
∴AB∥CD(内错角相等,两直线平行)
故答案为:已知;对顶角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.
28.【解答】解:(1)∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°﹣80°=100°,
∴∠ABP+∠PBN=100°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=100°,
∴∠CBD=∠CBP+∠DBP=50°;
(2)不变,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=100°,∠CBD=50°,
∴∠ABC+∠DBN=50°,
∴∠ABC=25°.
一、选择题(每小题3分,共36分)
1.(3分)﹣2019的相反数是( )
A.﹣2019 B.2019 C.﹣ D.
2.(3分)下列说法中错误的是( )
A.﹣x2y的系数是﹣ B.0是单项式
C.﹣x是一次单项式 D.xy2的次数是2
3.(3分)已知∠A=70°,则∠A的余角等于( )
A.70° B.20° C.110° D.10°
4.(3分)计算3a3﹣a3的结果是( )
A.2 B.2a C.2a3 D.3a3
5.(3分)中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图①表示的是(+2)+(﹣2),根据刘徵的这种表示法,可推算图②中所表示的算式为( )
A.(+3)+(+6) B.(﹣3)+(﹣6) C.(﹣3)+(+6) D.(+3)+(﹣6)
6.(3分)观察图形,下列说法正确的个数是( )
(1)直线BA和直线AB是同一条直线;
(2)AB+BD>AD;
(3)射线AC和射线AD是同一条射线;
(4)三条直线两两相交时,一定有三个交点.
A.1个 B.2个 C.3个 D.4个
7.(3分)若与﹣x2yn是同类项,则(﹣m)n的值为( )
A.8 B.﹣8 C.16 D.﹣16.
8.(3分)下列语句不正确的是( )
A.在同一平面内,过直线外一点有且只有一条直线与已知直线平行.
B.两直线被第三直线所截,如果同位角相等,那么两直线平行
C.两点确定一条直线
D.内错角相等
9.(3分)如图,在所标识的角中,互为对顶角的两个角是( )
A.∠1和∠2 B.∠1和∠4 C.∠2和∠3 D.∠3和∠4
10.(3分)如图,直线a、b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠1+∠2=180°
11.(3分)如图,直线a⊥直线c,直线b⊥直线c,若∠1=70°,则∠2=( )
A.70° B.90° C.110° D.80°
12.(3分)如图,A是直线l外一点,过点A作AB⊥l于点B,在直线l上取一点C,连结AC,使AC=2AB,P在线段BC上连结AP.若AB=3,则线段AP的长不可能是( )
A.3.5 B.4 C.5.5 D.6.5
二、填空题(每小题3分,共18分)
13.(3分)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 .
14.(3分)若代数式mx2+y2﹣5x2+5的值与字母x的取值无关,则m的值为 .
15.(3分)计算:48°39′+41°21'= °.
16.(3分)如图,射线OA表示西北方向,若射线OB表示南偏西60°的方向,则锐角∠AOB的大小是 度.
17.(3分)互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利20元,则这件商品的进价为 元.
18.(3分)已知线段AB=8cm,点C是线段AB所在直线上一点.下列说法:①若点C为线段AB的中点,则AC=4cm;②若AC=4cm,则点C为线段AB的中点;③AC>BC,则点C一定在线段AB的延长线上;④线段AC与BC的长度和一定不小于8cm,其中正确的有 (填写正确答案的序号).
三、解答题(共66分)
19.(8分)解方程:
(1)4x+3(2x﹣3)=12﹣(x﹣1)
(2)y﹣=2﹣
20.(6分)先化简,再求值:(4a2﹣2ab+b2)﹣3(a2﹣ab+b2),其中a=﹣1,b=﹣.
21.(6分)如图①,长方体的上下底面是边长为1的正方形,高为2;如图②,在5×5的正方形网格中,每个小方格都是边长为1的正方形.
(1)在图②中画出这个长方体的一个展开图;
(2)如果一只蚂蚁从顶点A处沿长方体表面爬行到顶点B处,请你在(1)中所画的展开图中画出该蚂蚁爬行的最短路线,并说明理由.
22.(6分)如果x=1是方程的解,
(1)求m的值;
(2)求关于y的方程m(y﹣3)﹣2=m(2y﹣5)的解.
23.(6分)如图,B、C两点把线段AD分成2:5:3的三部分,M为AD的中点,BM=9cm,求CM和AD的长.
24.(6分)如图,直线AB、CD相交于点O,过点O作OE⊥AB,OF平分∠BOD.
(1)直接写出∠AOC的补角;
(2)若∠AOC=40°,求∠EOF的度数.
25.(6分)如图,点D,点E分别在三角形ABC的边上,已知∠AED=∠ACB,DF,BE分别平分∠ADE,∠ABC,那么∠FDE与∠DEB相等吗?请说明理由.
26.(6分)某人原计划用26天生产一批零件,工作两天后因改变了操作方法,每天比原来多生产5个零件结果提前4天完成任务,问原来每天生产多少个零件?这批零件有多少个?
27.(8分)如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连接EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD∥BC和AB∥CD.
请完成下面的推理过程,并填空:
∵∠1=∠2( )
∠1=∠AGH( )
∴∠2=∠AGH( )
∴AD∥BC( )
∴∠ADE=∠C( )
∵∠A=∠C( )
∴∠ADE=∠A( )
∴AB∥CD( ).
28.(8分)如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
2018-2019学年湖南省长沙市岳麓区麓山国际实验学校七年级(下)开学数学试卷
参考答案与试题解析
一、选择题(每小题3分,共36分)
1.【解答】解:﹣2019的相反数是:2019.
故选:B.
2.【解答】解:该单项式是次数为3,故D错误;
故选:D.
3.【解答】解:∠A的余角:90°﹣70°=20°,
故选:B.
4.【解答】解:3a3﹣a3=2a3,
故选:C.
5.【解答】解:根据题意知,图②表示的数值为(+3)+(﹣6)=﹣3.
故选:D.
6.【解答】解:(1)直线BA和直线AB是同一条直线;正确,
(2)AB+BD>AD;正确
(3)射线AC和射线AD是同一条射线;正确,
(4)三条直线两两相交时,一定有三个交点,还可能有一个,故不正确.
共3个说法正确.
故选:C.
7.【解答】解:与﹣x2yn是同类项,
∴m﹣2=2,n=2,解得:m=4,n=2.
(﹣m)n=(﹣4)2=16.
故选:C.
8.【解答】解:A、在同一平面内,过直线外一点有且只有一条直线与已知直线平行,故A正确;
B、两直线被第三直线所截,如果同位角相等,那么两直线平行,故B正确;
C、两点确定一条直线,故C正确;
D、两直线平行,内错角相等,故D错误;
故选:D.
9.【解答】解:观察图形可知,互为对顶角的两个角是∠3和∠4.
故选:D.
10.【解答】解:由∠1=∠3,可得直线a与b平行,故A能判定;
由∠2+∠4=180°,∠2=∠5,∠4=∠3,可得∠3+∠5=180°,故直线a与b平行,故B能判定;
由∠1=∠4,∠4=∠3,可得∠1=∠3,故直线a与b平行,故C能判定;
由∠1+∠2=180°,不能判定直线a与b平行.
故选:D.
11.【解答】解:∵直线a⊥直线c,直线b⊥直线c,
∴a∥b,
∴∠1=∠3,
∵∠3=∠2,
∴∠2=∠1=70°.
故选:A.
12.【解答】解:∵过点A作AB⊥l于点B,AC=2AB,P在线段BC上连结AP,AB=3,
∴AC=6,
∴3≤AP≤6,
故AP不可能是6.5,
故选:D.
二、填空题(每小题3分,共18分)
13.【解答】解:能解释这一实际应用的数学知识是:两点确定一条直线,
故答案为:两点确定一条直线.
14.【解答】解:∵代数式mx2+y2﹣5x2+5的值与字母x的取值无关,
∴m﹣5=0,
解得:m=5.
故答案为:5.
15.【解答】解:原式=89°60′=90°,
故答案为:90.
16.【解答】解:由图可知:∠AOB=180°﹣45°﹣60°=75°.
故答案为:75.
17.【解答】解:设该商品的进价为x元,
根据题意得:200×0.5﹣x=20,
解得:x=80.
故答案为:80.
18.【解答】解:∵线段AB=8cm,点C是线段AB所在直线上一点,
∴①若点C为线段AB的中点,则AC=4cm是正确的;
②若AC=4cm,则点C为线段AB的中点或在线段AB的反向延长线上,原来的说法是错误的;
③AC>BC,则点C可能在线段AB上,原来的说法是错误的;
④线段AC与BC的长度和一定不小于8cm是正确的.
故答案为:①④.
三、解答题(共66分)
19.【解答】解:(1)去括号得:4x+6x﹣9=12﹣x+1,
移项,得:4x+6x+x=12+1+9,
合并同类项,得:11x=2,
系数化为1,得:x=2;
(2)去分母,得:10y﹣2(y+2)=10﹣5(y﹣3),
去括号,得:10y﹣2y﹣4=20﹣5y+15,
移项,得:10y﹣2y+5y=20+15+4,
合并同类项,得:13y=39,
系数化为1,得:y=3.
20.【解答】解:原式=4a2﹣2ab+b2﹣3a2+3ab﹣3b2
=a2+ab﹣2b2,
当a=﹣1,b=时,
原式=1+﹣
=1.
21.【解答】解:(1)其展开图如下图所示:
(2)如图所示,蚂蚁爬行的最短路线即为线段AB,
理由是:两点之间线段最短.
22.【解答】解:(1)将x=1代入方程得:2﹣(m﹣1)=2,
去分母得6﹣m+1=6,即m=1;
(2)将m=1代入方程得y﹣3﹣2=2y﹣5,
移项合并得:y=0.
23.【解答】解:设AB=2x(cm),BC=5x(cm),CD=3x(cm)
则AD=AB+BC+CD=10x(cm),
∵M是AD的中点
∴AM=MD=AD=5xcm
∴BM=AM﹣AB=5x﹣2x=3xcm
∵BM=9cm,
∴3x=9,
解得:x=3,
故CM=MD﹣CD=5x﹣3x=2x=2×3=6cm,
AD=10x=10×3=30(cm).
24.【解答】解:(1)∠AOC的补角是∠AOD,∠BOC;
(2)∵∠AOC=40°,
∴∠BOD=∠AOC=40°,
∵OF平分∠BOD,
∴∠BOF=20°,
∵OE⊥AB,
∴∠EOB=90°,
∴∠EOF=90°﹣20°=70°.
25.【解答】解:∠FDE=∠DEB,
理由:∵∠AED=∠ACB,
∴DE∥BC,
∴∠ADE=∠ABC,
∵DF,BE分别平分∠ADE,∠ABC,
∴∠ADF=∠ADE,∠ABE=∠ABC,
∴∠ADF=∠ABE,
∴DF∥BE,
∴∠FDE=∠DEB.
26.【解答】解:设原来每天生产x个零件,根据题意可得:
26x=2x+(x+5)×20,
解得:x=25,
故26×25=650(个).
答:原来每天生产25个零件,这批零件有650个.
27.【解答】证明:∵∠1=∠2(已知)
∠1=∠AGH(对顶角相等)
∴∠2=∠AGH(等量代换)
∴AD∥BC(同位角相等,两直线平行)
∴∠ADE=∠C(两直线平行,同位角相等)
∵∠A=∠C(已知)
∴∠ADE=∠A(等量代换)
∴AB∥CD(内错角相等,两直线平行)
故答案为:已知;对顶角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.
28.【解答】解:(1)∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°﹣80°=100°,
∴∠ABP+∠PBN=100°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=100°,
∴∠CBD=∠CBP+∠DBP=50°;
(2)不变,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=100°,∠CBD=50°,
∴∠ABC+∠DBN=50°,
∴∠ABC=25°.
同课章节目录
