华东师大版数学八年级下册 20.3数据的离散程度课件共22张PPT
文档属性
| 名称 | 华东师大版数学八年级下册 20.3数据的离散程度课件共22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-22 00:00:00 | ||
图片预览







文档简介
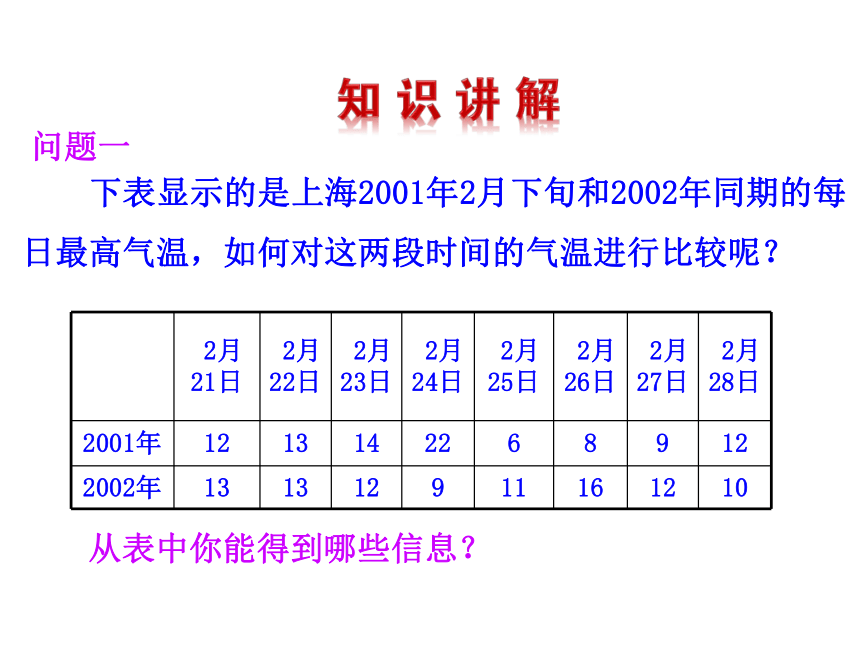
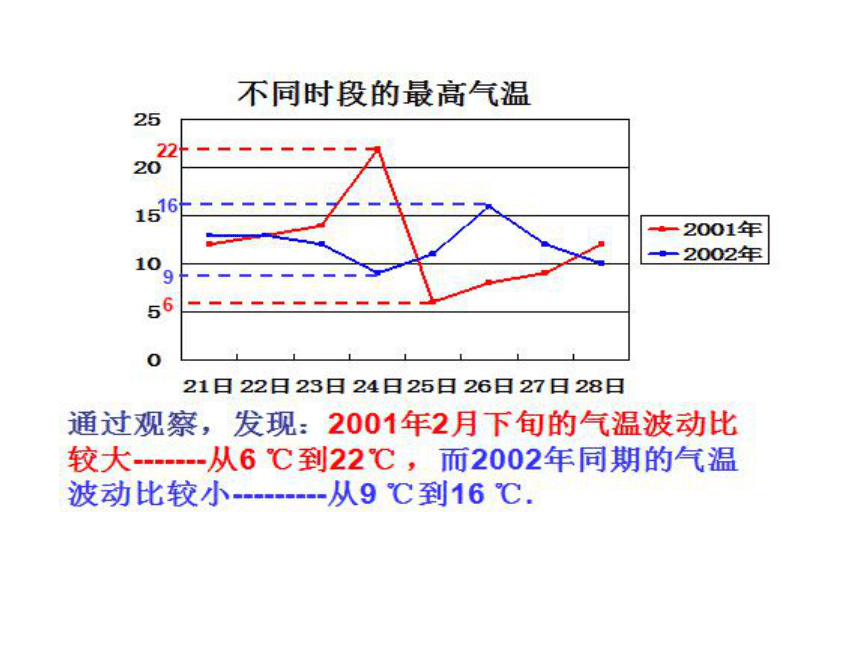
课件22张PPT。数据的离散程度华师版20.3 .1 方差平均数、众数、中位数的定义?众数:一组数据中出现次数最多的数值.中位数:将一组数据从小到大排列(或从大到小排列)处在中间位置的那个值.数据是偶数个时取中间两个数的平均数作为中位数.从表中你能得到哪些信息? 下表显示的是上海2001年2月下旬和2002年同期的每日最高气温,如何对这两段时间的气温进行比较呢?问题一 经计算可以看出,对于 2 月下旬的这段时间而言,2001年和2002年上海地区的平均气温相等,都是12°C. 比较两段时间气温的高低,求平均气温是一种常用的方法.这是不是说,两个时段的气温情况没有什么差异呢?观察图你感觉他们有没有差异呢? 小明和小兵两人参加体育项目训练,近期的五次测试成绩如表所示.谁的成绩较为稳定?为什么?问题二所以我们说小明的成绩比较稳定. 通过计算,我们发现两人测试成绩的平均值都是12.4分.从图可以看到:相比之下,小明的成绩大部分集中在平均数附近,而小兵的成绩与其平均值的离散程度略大.通常,如果一组数据与其平均值的离散程度较小,我们就说它比较稳定. 怎样的数能反映一组数据与其平均值的离散程度? 我们已经看出,小兵的测试成绩与平均值的偏差较大,而小明的较小.那么如何加以说明呢?可以直接将各数据与平均值的差进行累加吗?在表中写出你的计算结果.
通过计算,依据最后求和的结果可以比较两组数据围绕其平均值的波动情况吗?
如果不能,请你提出一个可行的方案1.6不能-2.40.6-0.40.60-1.4-1.42.61.6 -1.40-2.41.60.6-0.4 0.69.2-1.4 -1.42.61.6
-1.415.2如果一共进行了7次测试,小明因故缺席了两次,怎样比较谁的成绩更稳定?请将你的方法与数据填入表中.65平均130100120.49113990119938 我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况.这个结果通常称为方差.通常用s2表示一组数据的方差,用 x 表示一组数据的平均
数,x1,x2,…,xn表示各个数据.方差比较下列两组数据的方差:
A组:0, 10, 5, 5, 5, 5, 5, 5, 5, 5;
B组:4, 6, 3, 7, 2, 8, 1, 9, 5, 5解:先求平均数 求方差: 【跟踪训练】A的方差﹤B的方差1. 甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:则这四人中成绩发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁B2 .下列数据中,能用来刻画一组数据的离散程度的是( )
A.方差 B .中位数 C .平均数 D .众数
A甲3.为了考察甲、乙两种小麦的长势,分别从中抽出20株测得其高度,并求得它们的方差分别为 S甲 2 =3.6,S乙2 =15.8,则( )种小麦的长势比较整齐。解:因为S甲 2 =3.6, S乙2 =15.8,
所以S甲 2 < S乙2,
所以甲种小麦的长势较整齐。4. 甲、乙两人5次射击命中的环数如下:
甲 7 9 8 6 10
乙 7 8 9 8 8
则这两人5次射击命中的环数的平均数 甲= 乙=8,
方差 ____ .(填“>”“<”或“=”)>5.甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:(1)请填写下表:777.53(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看(分析谁的成绩好些);
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环及以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).通过本课的学习,需要我们掌握:2.能正确应用方差进行分析数据,并作出决策.1.理解方差的相关概念及计算公式,并能进行求值计算.谢谢
通过计算,依据最后求和的结果可以比较两组数据围绕其平均值的波动情况吗?
如果不能,请你提出一个可行的方案1.6不能-2.40.6-0.40.60-1.4-1.42.61.6 -1.40-2.41.60.6-0.4 0.69.2-1.4 -1.42.61.6
-1.415.2如果一共进行了7次测试,小明因故缺席了两次,怎样比较谁的成绩更稳定?请将你的方法与数据填入表中.65平均130100120.49113990119938 我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况.这个结果通常称为方差.通常用s2表示一组数据的方差,用 x 表示一组数据的平均
数,x1,x2,…,xn表示各个数据.方差比较下列两组数据的方差:
A组:0, 10, 5, 5, 5, 5, 5, 5, 5, 5;
B组:4, 6, 3, 7, 2, 8, 1, 9, 5, 5解:先求平均数 求方差: 【跟踪训练】A的方差﹤B的方差1. 甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:则这四人中成绩发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁B2 .下列数据中,能用来刻画一组数据的离散程度的是( )
A.方差 B .中位数 C .平均数 D .众数
A甲3.为了考察甲、乙两种小麦的长势,分别从中抽出20株测得其高度,并求得它们的方差分别为 S甲 2 =3.6,S乙2 =15.8,则( )种小麦的长势比较整齐。解:因为S甲 2 =3.6, S乙2 =15.8,
所以S甲 2 < S乙2,
所以甲种小麦的长势较整齐。4. 甲、乙两人5次射击命中的环数如下:
甲 7 9 8 6 10
乙 7 8 9 8 8
则这两人5次射击命中的环数的平均数 甲= 乙=8,
方差 ____ .(填“>”“<”或“=”)>5.甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:(1)请填写下表:777.53(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看(分析谁的成绩好些);
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环及以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).通过本课的学习,需要我们掌握:2.能正确应用方差进行分析数据,并作出决策.1.理解方差的相关概念及计算公式,并能进行求值计算.谢谢
