人教版九年级数学下28.2.2 解直角三角形应用举例—航海问题教学课件 共20张PPT
文档属性
| 名称 | 人教版九年级数学下28.2.2 解直角三角形应用举例—航海问题教学课件 共20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-18 00:00:00 | ||
图片预览








文档简介
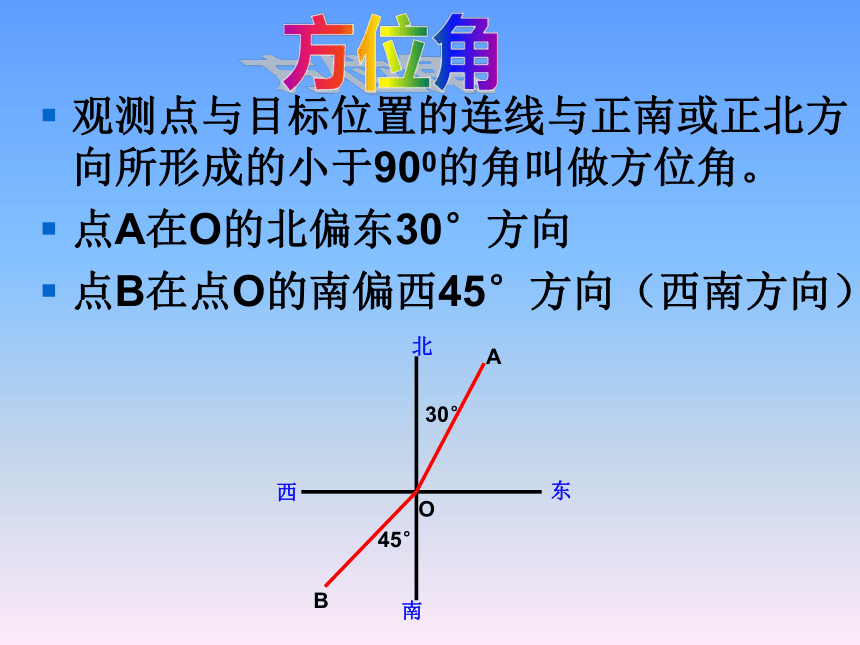
课件20张PPT。解直角三角形的应用(三)航海问题ABCbc1.三边关系3. 边角关系2.锐角关系导 回顾与思考观测点与目标位置的连线与正南或正北方向所形成的小于900的角叫做方位角。
点A在O的北偏东30°方向
点B在点O的南偏西45°方向(西南方向)
方位角例1:如图,一艘海轮位于灯塔P的北偏东600方向,
距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东300方向上的B处,这时,B处距离灯塔P有多远?(结果取整数)学600300ABPC解:?30030080海里∴cos∠APC?=在Rt△APC中,在Rt△BPC中,∠APC=300∴ PC =PA ·cos30°=∴∠PBC=300∴ PB =2PC =∴ PB ≈138.56≈139答:B处距离灯塔P约有139海里。归小结:利用解直角三角形的知识解决实际问题的一般过程是:(1) 将实际问题抽象为数学问题;
(画出平面图形,转化为解直角三角形的问题)(2) 根据问题中的条件,适当选用锐角三角函数或勾股定理解直角三角形;(3) 得到数学问题的答案;(4) 检验是否符合题意,得到实际问题的答案。北南西东船在什么位置离小岛最近呢?思考1垂线段最短货船继续向西航行途中会有触礁的危险吗?船有触礁的危险吗? 审题,画图。 茫茫大海中有一个小岛A,该岛四周16海里内有暗礁.今有货船由东向西航行,开始在距A岛30海里南偏东600的B处。A30海里这个问题归结为:在Rt△ABC中,已知∠A= 60°,斜边AB=30,求出AC的长与16比较大小。16海里●B思考2例2展海中有一个小岛A,它周围8千米内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东600方向上,航行12千米到达C点,这时测得小岛A在北偏东300方向上。如果渔船不改变航线继续向东航行,有没有触礁的危险?东北ABC60012千米300北?600300300解:过点A作AD⊥BC于点D,∠ABC=30 °, ∠ACD=60 °∴∠BAC=60°-30 °=30°∴AC=BC=12在Rt△ACD中,sin∠ACD=sin600=∴AD=AC· =6 ??≈10>8所以没有危险。12千米 如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?,航行24海里到C,见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?ABDCNN130?60?变式练习一2424ABDCNN145?60?如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?,航行24海里到C,见岛A在北偏西45?,货轮继续向西航行,有无触礁的危险?变式练习二如图:一艘轮船由海平面上A地出发向南偏西400的方向行驶40海里到达B地,再由B地向北偏西200的方向行驶40海里到达C地,则A,C两地的距离为 ____北A北BC40040海里D200有一个角是600的等腰三角形是等边三角形
你真棒!动动脑1.把实际问题转化成数学问题:一是将实际问题的图形转化为几何图形,画出正确的平面示意图,二是将已知条件转化为示意图中的边或角或它们之间的关系.2.把数学问题转化成解直角三角形问题,如果示意图不是
直角三角形,可添加适当的辅助线,构造直角三角形.方法小结:布置作业1、完成课后习题
2、拓展延伸练习(2019年·贵阳市模拟题一)某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到达,到达后必须立即卸货.此时,接到气象部门通知,一台风中心正以40海里/时的速度由A向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响.
(1)问:B处是否会受到台风的影响?请说明理由.
(2)为避免受到台风的影响,该船应在多少小时内卸完货物?课后拓展延伸结束寄语 悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.再见
点A在O的北偏东30°方向
点B在点O的南偏西45°方向(西南方向)
方位角例1:如图,一艘海轮位于灯塔P的北偏东600方向,
距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东300方向上的B处,这时,B处距离灯塔P有多远?(结果取整数)学600300ABPC解:?30030080海里∴cos∠APC?=在Rt△APC中,在Rt△BPC中,∠APC=300∴ PC =PA ·cos30°=∴∠PBC=300∴ PB =2PC =∴ PB ≈138.56≈139答:B处距离灯塔P约有139海里。归小结:利用解直角三角形的知识解决实际问题的一般过程是:(1) 将实际问题抽象为数学问题;
(画出平面图形,转化为解直角三角形的问题)(2) 根据问题中的条件,适当选用锐角三角函数或勾股定理解直角三角形;(3) 得到数学问题的答案;(4) 检验是否符合题意,得到实际问题的答案。北南西东船在什么位置离小岛最近呢?思考1垂线段最短货船继续向西航行途中会有触礁的危险吗?船有触礁的危险吗? 审题,画图。 茫茫大海中有一个小岛A,该岛四周16海里内有暗礁.今有货船由东向西航行,开始在距A岛30海里南偏东600的B处。A30海里这个问题归结为:在Rt△ABC中,已知∠A= 60°,斜边AB=30,求出AC的长与16比较大小。16海里●B思考2例2展海中有一个小岛A,它周围8千米内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东600方向上,航行12千米到达C点,这时测得小岛A在北偏东300方向上。如果渔船不改变航线继续向东航行,有没有触礁的危险?东北ABC60012千米300北?600300300解:过点A作AD⊥BC于点D,∠ABC=30 °, ∠ACD=60 °∴∠BAC=60°-30 °=30°∴AC=BC=12在Rt△ACD中,sin∠ACD=sin600=∴AD=AC· =6 ??≈10>8所以没有危险。12千米 如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?,航行24海里到C,见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?ABDCNN130?60?变式练习一2424ABDCNN145?60?如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?,航行24海里到C,见岛A在北偏西45?,货轮继续向西航行,有无触礁的危险?变式练习二如图:一艘轮船由海平面上A地出发向南偏西400的方向行驶40海里到达B地,再由B地向北偏西200的方向行驶40海里到达C地,则A,C两地的距离为 ____北A北BC40040海里D200有一个角是600的等腰三角形是等边三角形
你真棒!动动脑1.把实际问题转化成数学问题:一是将实际问题的图形转化为几何图形,画出正确的平面示意图,二是将已知条件转化为示意图中的边或角或它们之间的关系.2.把数学问题转化成解直角三角形问题,如果示意图不是
直角三角形,可添加适当的辅助线,构造直角三角形.方法小结:布置作业1、完成课后习题
2、拓展延伸练习(2019年·贵阳市模拟题一)某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到达,到达后必须立即卸货.此时,接到气象部门通知,一台风中心正以40海里/时的速度由A向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响.
(1)问:B处是否会受到台风的影响?请说明理由.
(2)为避免受到台风的影响,该船应在多少小时内卸完货物?课后拓展延伸结束寄语 悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.再见
