人教版九年级数学上册24.3正多边形和圆课件34张PPT
文档属性
| 名称 | 人教版九年级数学上册24.3正多边形和圆课件34张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 680.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-18 00:00:00 | ||
图片预览



文档简介
课件34张PPT。24.3正多边形和圆各边相等,各角也相等的多边形叫做正多边形
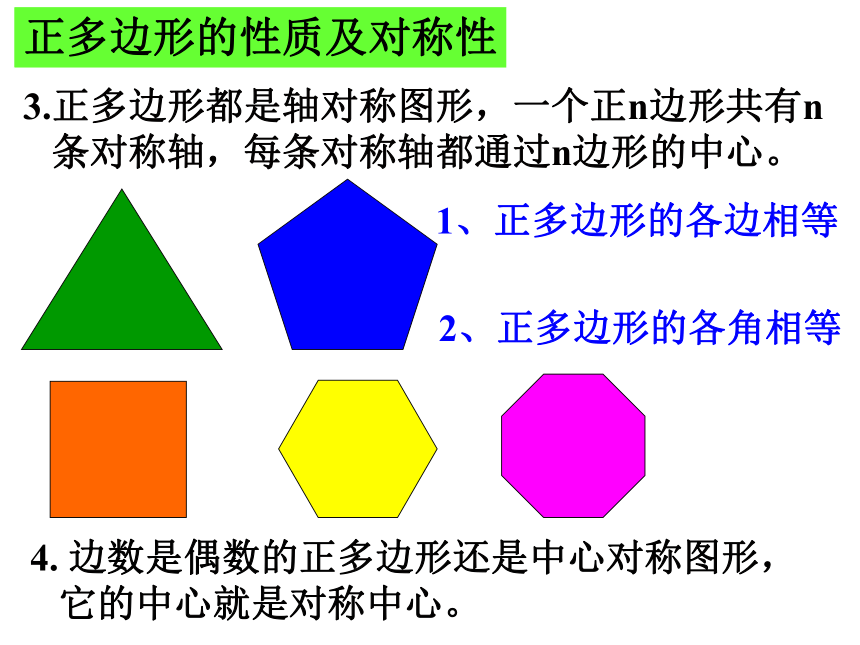
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形。三条边相等三个角相等(60度)。四条边相等四个角相等(900)一 .正多边形定义问题1,什么样的图形是正多边形?各边相等,各角也相等的多边形是正多边形.练习:1. 矩形是正多边形吗?菱形呢?正方形呢?为什么?矩形不是正多边形,因为四条边不都相等;菱形不是正多边形,因为菱形的四个角不都相等;正方形是正多边形.因为四条边都相等,四个角都相等.3.正多边形都是轴对称图形,一个正n边形共有n
条对称轴,每条对称轴都通过n边形的中心。正多边形的性质及对称性4. 边数是偶数的正多边形还是中心对称图形,
它的中心就是对称中心。1、正多边形的各边相等2、正多边形的各角相等正n边形与圆的关系1.把正n边形的边数无限增多,就接近于圆.2.怎样由圆得到多边形呢?ABCD思考1: 把一个圆4等分, 并依次连
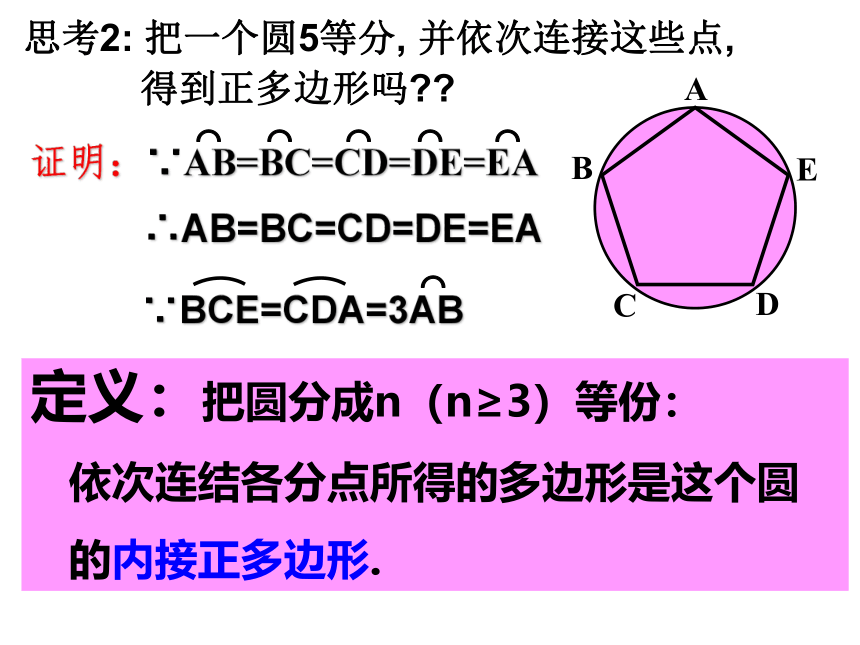
接这些点,得到正多边形吗??弧相等弦相等(多边形的边相等)圆周角相等(多边形的角相等)—多边形是正多边形思考2: 把一个圆5等分, 并依次连接这些点,
得到正多边形吗??证明:∵AB=BC=CD=DE=EAABCDE⌒⌒⌒⌒⌒∴AB=BC=CD=DE=EA∵BCE=CDA=3AB⌒∴∠A=∠B同理∠B=∠C=∠D=∠E∴∠A=∠B=∠C=∠D=∠E又∵顶点A、B、C、D、E都在⊙O上∴五边形ABCDE是⊙O的 内接正五边形.定义:把圆分成n(n≥3)等份:
依次连结各分点所得的多边形是这个圆
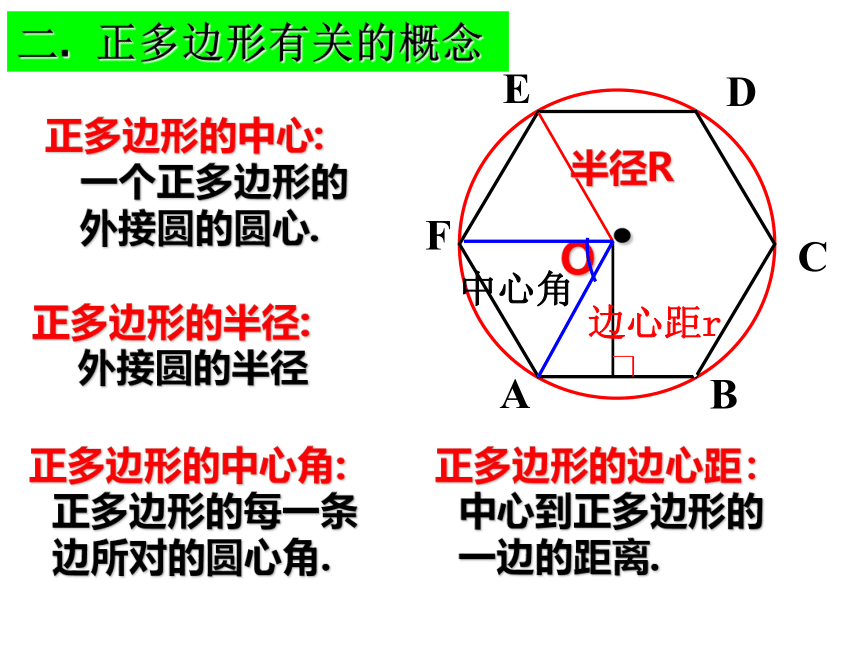
的内接正多边形..O中心角半径R边心距r正多边形的中心:
一个正多边形的
外接圆的圆心.正多边形的半径:
外接圆的半径正多边形的中心角:
正多边形的每一条
边所对的圆心角.正多边形的边心距:
中心到正多边形的
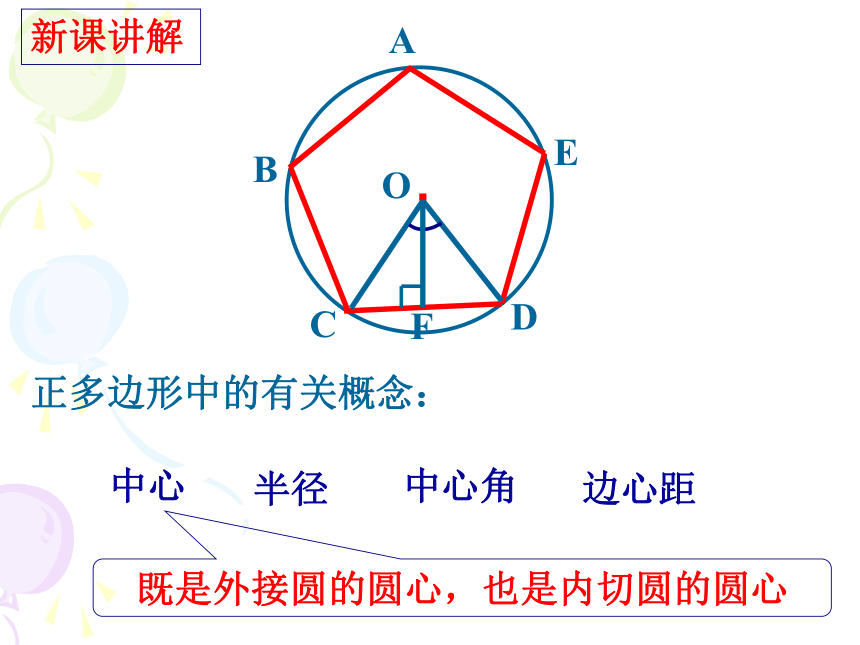
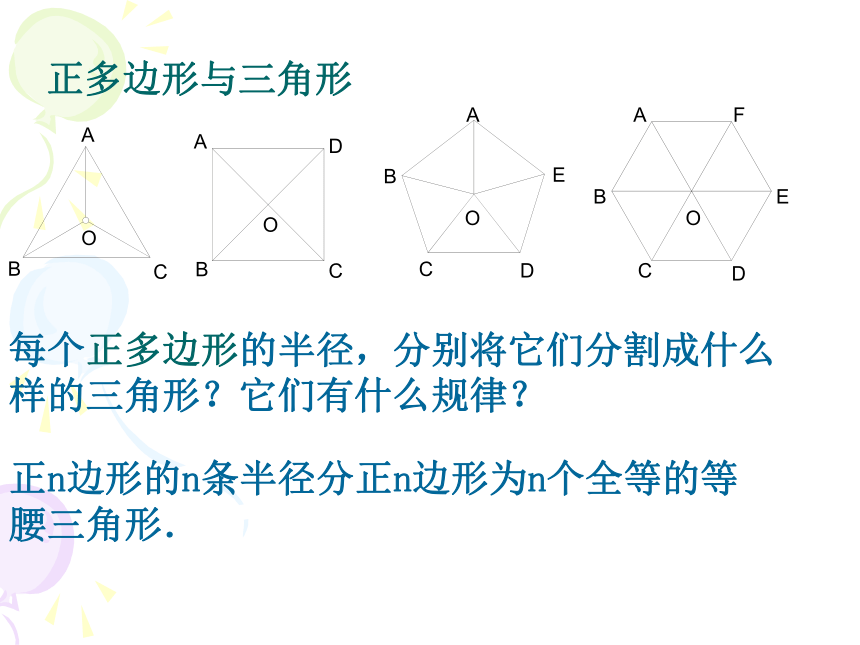
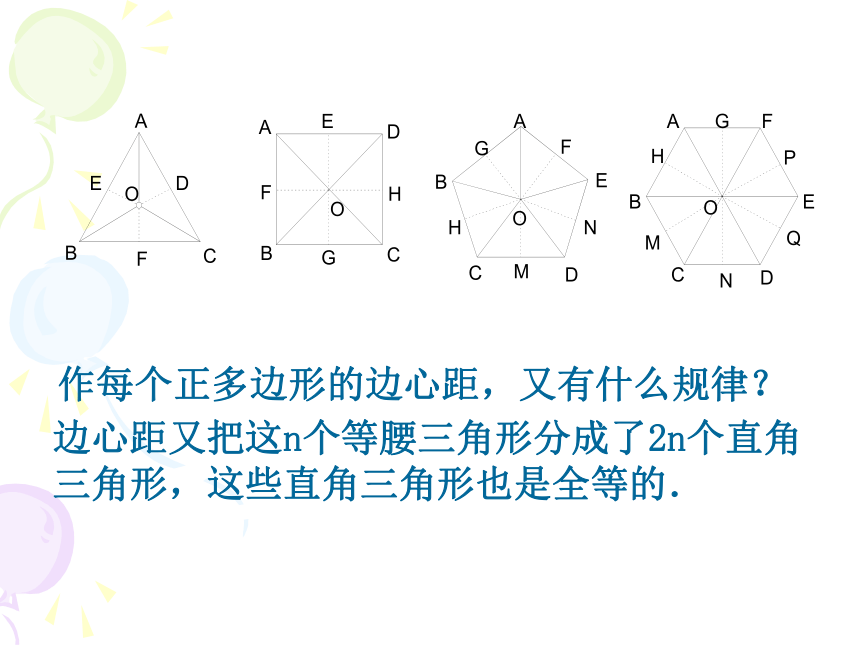
一边的距离.二. 正多边形有关的概念AB新课讲解中心半径中心角边心距正多边形中的有关概念:既是外接圆的圆心,也是内切圆的圆心每个正多边形的半径,分别将它们分割成什么样的三角形?它们有什么规律? 正n边形的n条半径分正n边形为n个全等的等腰三角形. 正多边形与三角形作每个正多边形的边心距,又有什么规律? 边心距又把这n个等腰三角形分成了2n个直角
三角形,这些直角三角形也是全等的.
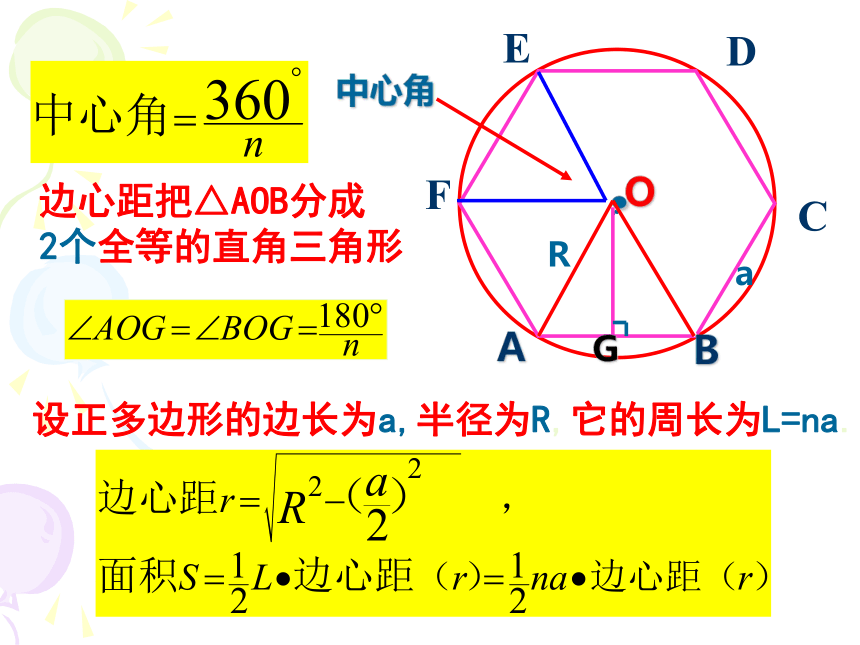
.O中心角ABG边心距把△AOB分成
2个全等的直角三角形设正多边形的边长为a,半径为R,它的周长为L=na.Ra新课讲解
正n边形的一个内角的
度数是____________;
中心角是___________;
正多边形的中心角与外角的大小关系是________.相等抢答题:1.o是正
与 的圆心。△ABC的中心,它是△ABC的2、OB叫正△ABC的
它是正△ABC的 的半径。 3、OD叫作正△ABC的 它是正△ABC的 的半径。D半径外接圆边心距内切圆外接圆内切圆4、正方形ABCD的外接圆圆心O叫做
正方形ABCD的5、正方形ABCD的内切圆的半径OE叫做
正方形ABCD的ABCD.OE中心边心距6、⊙O是正五边形ABCDE的外接圆,弦AB的
弦心距OF叫正五边形ABCDE的 ,
它是正五边形ABCDE的 圆的半径。7、 ∠AOB叫做正五边形ABCDE的 角,
它的度数是边心距内切中心72度8、图中正六边形ABCDEF的中心角是( )
它的度数是( )9、你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么? BA∠AOB60度解答:正六边形的半径与边长数量关系是相等因为:正六边形的中心角
是60度和半径组成的三角
形是等边三角形,所以边
长与半径相等。例1、 有一个亭子它的地基是半径为4m的正六边形, 求地基的周长和面积.OBCrRP∴亭子的周长 L=6×4=24(m).OBCrR=4P例2、如图:已知正六边形ABCDEF的边长为6cm,(1)求正六边形ABCDEF的外接圆的半径。(2)求正六边形ABCDEF的边心距。作半径OA、OB;∵OA=OB,∠AOB=60° ∴△OAB是正三角形,R=AB=6cm, HR解:(1)(2)作OG⊥AB于H,得Rt△OHB.练习:已知正六边形ABCDEF的的边心距为
r =6cm,求正六边形ABCDEF的外接圆的半径R。ABCODS3例4: 已知正六边形ABCDEF的半径为R,求这个正六边形的边长a6、周长l6、面积S6 .ABCDEFOG例5:如图,M,N分别是⊙O内接正多边形AB,BC上的点,且BM=CN.
(1)求图①中∠MON的度数;
(2)图②中∠MON= ;
图③中∠MON= ;
(3)试探究∠MON的度数与正n边形的边数n的关系.;四边形MONB的面积与正n边形面积之间的关系...ABCMNMNMNOOO当堂训练1.课本P108第1题1.圆内接正方形的半径:边心距:边长________
2. 圆内接正六边形的边长是8 cm用么该正六边形的半径为________;边心距_____.
3.正多边形的中心角与该正多边形一个内角的关系是-------
4.若一个正多边形的每一个外角都等于36°,那么这个正多边形的中心角为------练习;巩固提高:
5. 边长为a的正三角形的高h=_____,外接圆半径R=_____,内切圆半径r=______
6.分别求半径为R的圆内接正三角形、正方形的边长、边心距和面积。
7、若同一个圆的内接三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3:r4:r6=____________
7、如图,正六边形ABCDEF中,阴影部分的面积为 ,则此正六边形的边长为_______怎样画一个正多边形呢?
问题1:已知⊙O的半径为2cm,求作圆的内接正三角形.
120 °①用量角器度量,使∠AOB=∠BOC=∠COA=120°.
②用量角器或30°角的三角板度量,使∠BAO=∠oAc=30°.
AOCB你能用以上方法画出正四边形、正五边形、正六边形吗?·ABCDOOABCDEF·90°72°60°你能尺规作出正六边形、正三角形、正十二边形吗?OABCEF·D 以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形……… 定理:
把圆分成n(n≥3)等份:
⑴依次连结各分点所得的多边形是这个圆的
内接正多边形;
⑵经过各分点作圆的切线,以相邻切线的交
点为顶点的多边形是这个圆的外切正多边
形。ABCDEO如图:
已知点A、B、C、D、E是⊙O 的5等分点,画出⊙O的内接和外切正五边形 说说作正多边形的方法有哪些?归纳
(1)用量角器等分圆周作正n边形;
(2)用尺规作正方形及由此扩展作正八边形, 用尺规作正六边形及由此扩展作正12边形、正三角形.
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形。三条边相等三个角相等(60度)。四条边相等四个角相等(900)一 .正多边形定义问题1,什么样的图形是正多边形?各边相等,各角也相等的多边形是正多边形.练习:1. 矩形是正多边形吗?菱形呢?正方形呢?为什么?矩形不是正多边形,因为四条边不都相等;菱形不是正多边形,因为菱形的四个角不都相等;正方形是正多边形.因为四条边都相等,四个角都相等.3.正多边形都是轴对称图形,一个正n边形共有n
条对称轴,每条对称轴都通过n边形的中心。正多边形的性质及对称性4. 边数是偶数的正多边形还是中心对称图形,
它的中心就是对称中心。1、正多边形的各边相等2、正多边形的各角相等正n边形与圆的关系1.把正n边形的边数无限增多,就接近于圆.2.怎样由圆得到多边形呢?ABCD思考1: 把一个圆4等分, 并依次连
接这些点,得到正多边形吗??弧相等弦相等(多边形的边相等)圆周角相等(多边形的角相等)—多边形是正多边形思考2: 把一个圆5等分, 并依次连接这些点,
得到正多边形吗??证明:∵AB=BC=CD=DE=EAABCDE⌒⌒⌒⌒⌒∴AB=BC=CD=DE=EA∵BCE=CDA=3AB⌒∴∠A=∠B同理∠B=∠C=∠D=∠E∴∠A=∠B=∠C=∠D=∠E又∵顶点A、B、C、D、E都在⊙O上∴五边形ABCDE是⊙O的 内接正五边形.定义:把圆分成n(n≥3)等份:
依次连结各分点所得的多边形是这个圆
的内接正多边形..O中心角半径R边心距r正多边形的中心:
一个正多边形的
外接圆的圆心.正多边形的半径:
外接圆的半径正多边形的中心角:
正多边形的每一条
边所对的圆心角.正多边形的边心距:
中心到正多边形的
一边的距离.二. 正多边形有关的概念AB新课讲解中心半径中心角边心距正多边形中的有关概念:既是外接圆的圆心,也是内切圆的圆心每个正多边形的半径,分别将它们分割成什么样的三角形?它们有什么规律? 正n边形的n条半径分正n边形为n个全等的等腰三角形. 正多边形与三角形作每个正多边形的边心距,又有什么规律? 边心距又把这n个等腰三角形分成了2n个直角
三角形,这些直角三角形也是全等的.
.O中心角ABG边心距把△AOB分成
2个全等的直角三角形设正多边形的边长为a,半径为R,它的周长为L=na.Ra新课讲解
正n边形的一个内角的
度数是____________;
中心角是___________;
正多边形的中心角与外角的大小关系是________.相等抢答题:1.o是正
与 的圆心。△ABC的中心,它是△ABC的2、OB叫正△ABC的
它是正△ABC的 的半径。 3、OD叫作正△ABC的 它是正△ABC的 的半径。D半径外接圆边心距内切圆外接圆内切圆4、正方形ABCD的外接圆圆心O叫做
正方形ABCD的5、正方形ABCD的内切圆的半径OE叫做
正方形ABCD的ABCD.OE中心边心距6、⊙O是正五边形ABCDE的外接圆,弦AB的
弦心距OF叫正五边形ABCDE的 ,
它是正五边形ABCDE的 圆的半径。7、 ∠AOB叫做正五边形ABCDE的 角,
它的度数是边心距内切中心72度8、图中正六边形ABCDEF的中心角是( )
它的度数是( )9、你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么? BA∠AOB60度解答:正六边形的半径与边长数量关系是相等因为:正六边形的中心角
是60度和半径组成的三角
形是等边三角形,所以边
长与半径相等。例1、 有一个亭子它的地基是半径为4m的正六边形, 求地基的周长和面积.OBCrRP∴亭子的周长 L=6×4=24(m).OBCrR=4P例2、如图:已知正六边形ABCDEF的边长为6cm,(1)求正六边形ABCDEF的外接圆的半径。(2)求正六边形ABCDEF的边心距。作半径OA、OB;∵OA=OB,∠AOB=60° ∴△OAB是正三角形,R=AB=6cm, HR解:(1)(2)作OG⊥AB于H,得Rt△OHB.练习:已知正六边形ABCDEF的的边心距为
r =6cm,求正六边形ABCDEF的外接圆的半径R。ABCODS3例4: 已知正六边形ABCDEF的半径为R,求这个正六边形的边长a6、周长l6、面积S6 .ABCDEFOG例5:如图,M,N分别是⊙O内接正多边形AB,BC上的点,且BM=CN.
(1)求图①中∠MON的度数;
(2)图②中∠MON= ;
图③中∠MON= ;
(3)试探究∠MON的度数与正n边形的边数n的关系.;四边形MONB的面积与正n边形面积之间的关系...ABCMNMNMNOOO当堂训练1.课本P108第1题1.圆内接正方形的半径:边心距:边长________
2. 圆内接正六边形的边长是8 cm用么该正六边形的半径为________;边心距_____.
3.正多边形的中心角与该正多边形一个内角的关系是-------
4.若一个正多边形的每一个外角都等于36°,那么这个正多边形的中心角为------练习;巩固提高:
5. 边长为a的正三角形的高h=_____,外接圆半径R=_____,内切圆半径r=______
6.分别求半径为R的圆内接正三角形、正方形的边长、边心距和面积。
7、若同一个圆的内接三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3:r4:r6=____________
7、如图,正六边形ABCDEF中,阴影部分的面积为 ,则此正六边形的边长为_______怎样画一个正多边形呢?
问题1:已知⊙O的半径为2cm,求作圆的内接正三角形.
120 °①用量角器度量,使∠AOB=∠BOC=∠COA=120°.
②用量角器或30°角的三角板度量,使∠BAO=∠oAc=30°.
AOCB你能用以上方法画出正四边形、正五边形、正六边形吗?·ABCDOOABCDEF·90°72°60°你能尺规作出正六边形、正三角形、正十二边形吗?OABCEF·D 以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形……… 定理:
把圆分成n(n≥3)等份:
⑴依次连结各分点所得的多边形是这个圆的
内接正多边形;
⑵经过各分点作圆的切线,以相邻切线的交
点为顶点的多边形是这个圆的外切正多边
形。ABCDEO如图:
已知点A、B、C、D、E是⊙O 的5等分点,画出⊙O的内接和外切正五边形 说说作正多边形的方法有哪些?归纳
(1)用量角器等分圆周作正n边形;
(2)用尺规作正方形及由此扩展作正八边形, 用尺规作正六边形及由此扩展作正12边形、正三角形.
同课章节目录
