18.2平行四边形的判定(第一课时)课件(21张PPT)(新版)华东师大版
文档属性
| 名称 | 18.2平行四边形的判定(第一课时)课件(21张PPT)(新版)华东师大版 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-18 14:19:05 | ||
图片预览





文档简介
课件21张PPT。HS八(下)
教学课件第18章 平行四边形18.2 平行四边形的判定第1课时 平行四边形的判定定理1,2学习目标1.经历平行四边形判定定理的猜想与证明过程,体会
类比思想及探究图形判定方法的一般思路.(重点)
2.掌握平行四边形的判定定理1和2,能根据不同条件
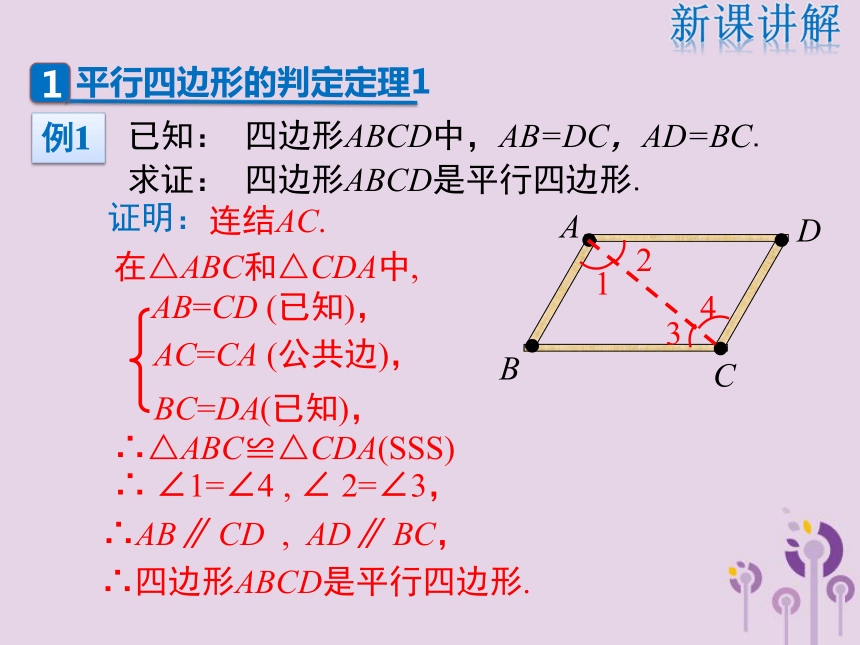
灵活选取适当的判定定理进行推理论证.(难点) 数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样确保它们平行的呢?新课导入只要使互相平行的夹在铁轨之间的枕木长相等就可以了.那这是为什么呢?会不会跟我们学过的平行四边形有关呢?新课导入 已知: 四边形ABCD中,AB=DC,AD=BC.
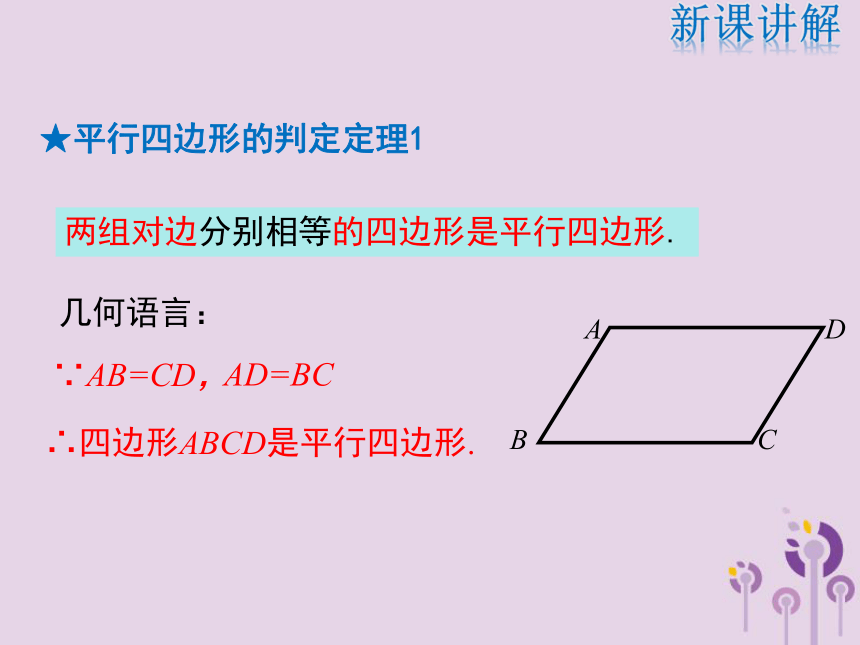
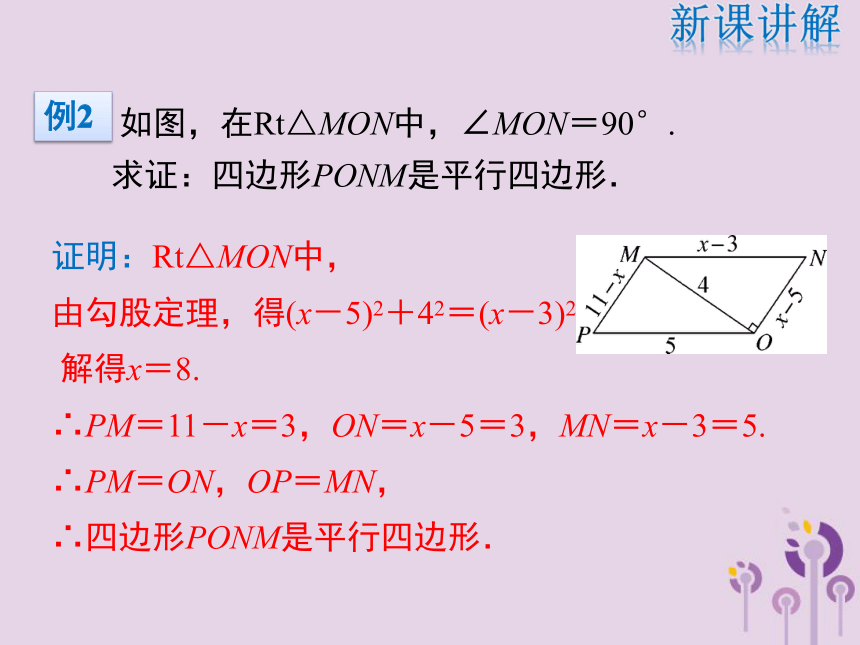
求证: 四边形ABCD是平行四边形.连结AC.在△ABC和△CDA中,AB=CD (已知),BC=DA(已知),AC=CA (公共边),∴△ABC≌△CDA(SSS)∴ ∠1=∠4 , ∠ 2=∠3,∴AB∥ CD , AD∥ BC,∴四边形ABCD是平行四边形.证明:新课讲解平行四边形的判定定理1例1两组对边分别相等的四边形是平行四边形.∵AB=CD,AD=BC∴四边形ABCD是平行四边形.几何语言:BDCA新课讲解★平行四边形的判定定理1 如图,在Rt△MON中,∠MON=90°.
求证:四边形PONM是平行四边形.证明:Rt△MON中,
由勾股定理,得(x-5)2+42=(x-3)2,
解得x=8.
∴PM=11-x=3,ON=x-5=3,MN=x-3=5.
∴PM=ON,OP=MN,
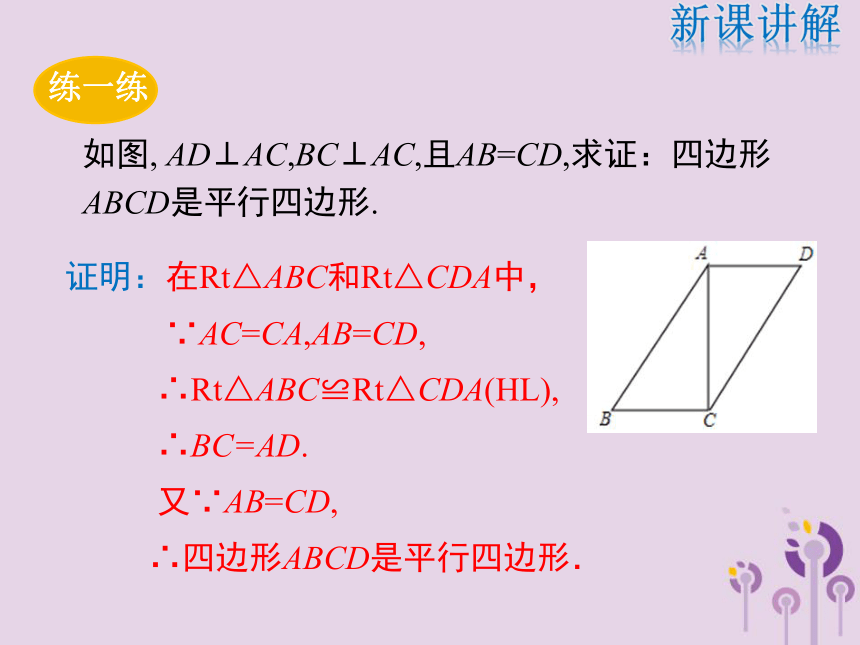
∴四边形PONM是平行四边形.新课讲解例2如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.证明:在Rt△ABC和Rt△CDA中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=AD.
又∵AB=CD,
∴四边形ABCD是平行四边形.新课讲解两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?猜想1:一组对边相等的四边形是平行四边形.等腰梯形不是平行四边形,因而此猜想错误.猜想2:一组对边平行的四边形是平行四边形.梯形的上下底平行,但不是平行四边形,因而此猜想错误.新课讲解平行四边形的判定定理2BA如图,将线段AB向右平移BC长度后得到线段DC,连结AD、BC,由此你能猜想四边形ABCD的形状吗?DC四边形ABCD是平行四边形猜想3:一组对边平行且相等的四边形是平行四边形.你能证明吗?新课讲解证明思路作对角线构造全等三角形一组对应边相等两组对边分别相等四边形ABCD是平行四边形如图,在四边形ABCD中,AB=CD且AB∥CD.
求证:四边形ABCD是平行四边形.新课讲解证明:连结AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,AB=CD, AC=CA,∠1=∠2,∴△ABC≌△CDA(SAS),∴BC=DA .
又∵AB= CD, ∴四边形ABCD是平行四边形.新课讲解一组对边平行且相等的四边形是平行四边形.∵AB=CD,AB∥CD∴四边形ABCD是平行四边形.几何语言:BDCA新课讲解★平行四边形的判定定理2证明:∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形. 如图 ,在平行四边形ABCD中,E、F分别是AB、CD的中点.求证:四边形EBFD是平行四边形. 新课讲解例3 如图,点A、B、C、D在同一条直线上,点E、
F分别在直线AD的两侧,AE=DF,∠A=∠D,
AB=DC.求证:四边形BFCE是平行四边形.证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=DB ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS),
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.新课讲解例4 已知四边形ABCD中有四个条件:AB∥CD,AB=CD,
BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的是 ( )
A.AB∥CD,AB=CD
B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD
D.AB=CD,BC=AD C新课讲解1. 如图所示,△ABC是等边三角形,P是其内任意一
点,PD//AB,PE//BC,PF//AC,若△ABC的周长为24,
则PD+PE+PF= . 82.已知AD//BC ,要使这个四边形
ABCD为平行四边形,需要增
加条件_____ . AD=BC或AB//CD 随堂即练3.已知:如图,E、F分别是 平行四边形
ABCD 的边AD、BC的中点.
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AB∥CD, AD=BC.∵E、F分别是AD,BC的中点,∴ED=BF.∴四边形EBFD是平行四边形(一组对边平行并且相等的四边形是平行四边形).∴BE=DF(平行四边形的对边分别相等).随堂即练4.如图,已知E、F、G、H分别是?ABCD的边AB、
BC、CD、DA上的点,且AE=CG,BF=DH.
求证:四边形EFGH是平行四边形.证明:在平行四边形ABCD中,
∠A=∠C,AD=BC.
又∵BF=DH,
∴AH=CF.
又∵AE=CG,
∴△AEH≌△CGF(SAS),
∴EH=GF.
同理得△BEF≌△DGH(SAS),
∴GH=EF,
∴四边形EFGH是平行四边形.随堂即练平行四边形的判定判定定理1判定定理2两组对边分别相等的四边形是平行四边形一组对边平行且相等的四边形是平行四边形课堂总结
教学课件第18章 平行四边形18.2 平行四边形的判定第1课时 平行四边形的判定定理1,2学习目标1.经历平行四边形判定定理的猜想与证明过程,体会
类比思想及探究图形判定方法的一般思路.(重点)
2.掌握平行四边形的判定定理1和2,能根据不同条件
灵活选取适当的判定定理进行推理论证.(难点) 数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样确保它们平行的呢?新课导入只要使互相平行的夹在铁轨之间的枕木长相等就可以了.那这是为什么呢?会不会跟我们学过的平行四边形有关呢?新课导入 已知: 四边形ABCD中,AB=DC,AD=BC.
求证: 四边形ABCD是平行四边形.连结AC.在△ABC和△CDA中,AB=CD (已知),BC=DA(已知),AC=CA (公共边),∴△ABC≌△CDA(SSS)∴ ∠1=∠4 , ∠ 2=∠3,∴AB∥ CD , AD∥ BC,∴四边形ABCD是平行四边形.证明:新课讲解平行四边形的判定定理1例1两组对边分别相等的四边形是平行四边形.∵AB=CD,AD=BC∴四边形ABCD是平行四边形.几何语言:BDCA新课讲解★平行四边形的判定定理1 如图,在Rt△MON中,∠MON=90°.
求证:四边形PONM是平行四边形.证明:Rt△MON中,
由勾股定理,得(x-5)2+42=(x-3)2,
解得x=8.
∴PM=11-x=3,ON=x-5=3,MN=x-3=5.
∴PM=ON,OP=MN,
∴四边形PONM是平行四边形.新课讲解例2如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.证明:在Rt△ABC和Rt△CDA中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=AD.
又∵AB=CD,
∴四边形ABCD是平行四边形.新课讲解两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?猜想1:一组对边相等的四边形是平行四边形.等腰梯形不是平行四边形,因而此猜想错误.猜想2:一组对边平行的四边形是平行四边形.梯形的上下底平行,但不是平行四边形,因而此猜想错误.新课讲解平行四边形的判定定理2BA如图,将线段AB向右平移BC长度后得到线段DC,连结AD、BC,由此你能猜想四边形ABCD的形状吗?DC四边形ABCD是平行四边形猜想3:一组对边平行且相等的四边形是平行四边形.你能证明吗?新课讲解证明思路作对角线构造全等三角形一组对应边相等两组对边分别相等四边形ABCD是平行四边形如图,在四边形ABCD中,AB=CD且AB∥CD.
求证:四边形ABCD是平行四边形.新课讲解证明:连结AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,AB=CD, AC=CA,∠1=∠2,∴△ABC≌△CDA(SAS),∴BC=DA .
又∵AB= CD, ∴四边形ABCD是平行四边形.新课讲解一组对边平行且相等的四边形是平行四边形.∵AB=CD,AB∥CD∴四边形ABCD是平行四边形.几何语言:BDCA新课讲解★平行四边形的判定定理2证明:∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形. 如图 ,在平行四边形ABCD中,E、F分别是AB、CD的中点.求证:四边形EBFD是平行四边形. 新课讲解例3 如图,点A、B、C、D在同一条直线上,点E、
F分别在直线AD的两侧,AE=DF,∠A=∠D,
AB=DC.求证:四边形BFCE是平行四边形.证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=DB ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS),
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.新课讲解例4 已知四边形ABCD中有四个条件:AB∥CD,AB=CD,
BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的是 ( )
A.AB∥CD,AB=CD
B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD
D.AB=CD,BC=AD C新课讲解1. 如图所示,△ABC是等边三角形,P是其内任意一
点,PD//AB,PE//BC,PF//AC,若△ABC的周长为24,
则PD+PE+PF= . 82.已知AD//BC ,要使这个四边形
ABCD为平行四边形,需要增
加条件_____ . AD=BC或AB//CD 随堂即练3.已知:如图,E、F分别是 平行四边形
ABCD 的边AD、BC的中点.
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AB∥CD, AD=BC.∵E、F分别是AD,BC的中点,∴ED=BF.∴四边形EBFD是平行四边形(一组对边平行并且相等的四边形是平行四边形).∴BE=DF(平行四边形的对边分别相等).随堂即练4.如图,已知E、F、G、H分别是?ABCD的边AB、
BC、CD、DA上的点,且AE=CG,BF=DH.
求证:四边形EFGH是平行四边形.证明:在平行四边形ABCD中,
∠A=∠C,AD=BC.
又∵BF=DH,
∴AH=CF.
又∵AE=CG,
∴△AEH≌△CGF(SAS),
∴EH=GF.
同理得△BEF≌△DGH(SAS),
∴GH=EF,
∴四边形EFGH是平行四边形.随堂即练平行四边形的判定判定定理1判定定理2两组对边分别相等的四边形是平行四边形一组对边平行且相等的四边形是平行四边形课堂总结
