苏科版七年级数学下册7.4 认识三角形第一课时课件(25张PPT)
文档属性
| 名称 | 苏科版七年级数学下册7.4 认识三角形第一课时课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 652.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-21 00:00:00 | ||
图片预览




文档简介
课件25张PPT。认识三角形(1)
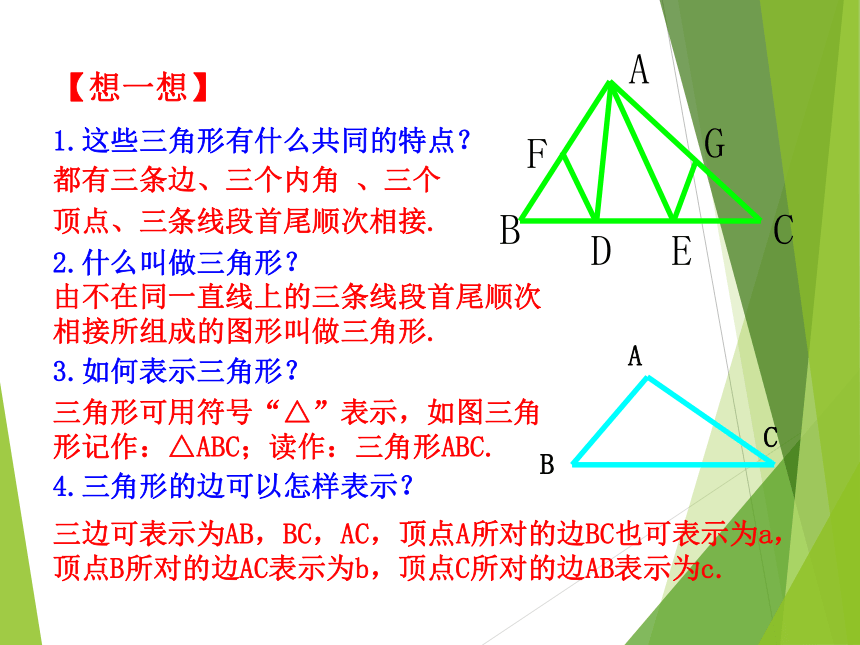
2019.3.17都有三条边、三个内角 、三个
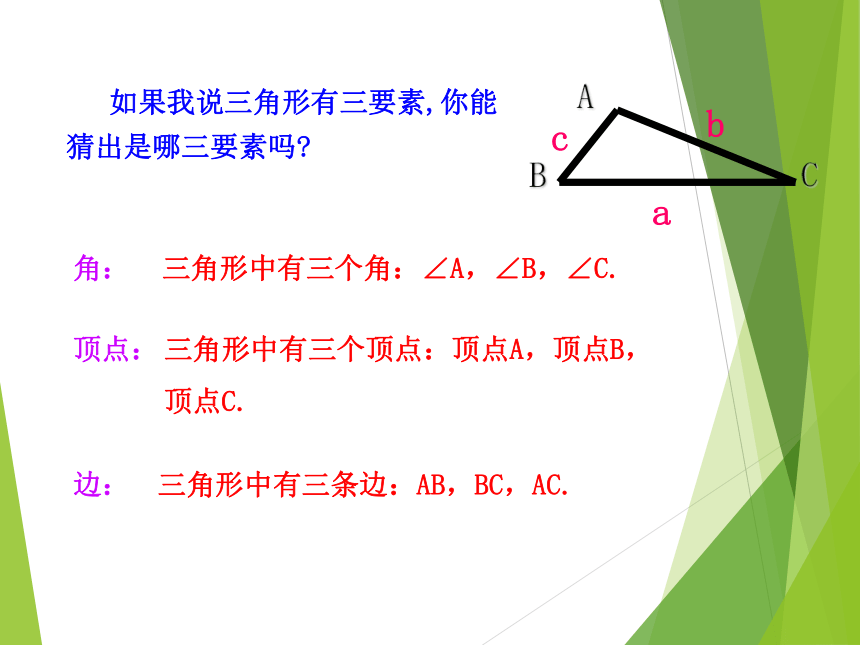
顶点、三条线段首尾顺次相接.1.这些三角形有什么共同的特点?ABCDEFG由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.什么叫做三角形?3.如何表示三角形?三角形可用符号“△”表示,如图三角形记作:△ABC;读作:三角形ABC.4.三角形的边可以怎样表示?三边可表示为AB,BC,AC,顶点A所对的边BC也可表示为a,顶点B所对的边AC表示为b,顶点C所对的边AB表示为c.【想一想】边:三角形中有三条边:AB,BC,AC.角:三角形中有三个角:∠A,∠B,∠C.顶点:三角形中有三个顶点:顶点A,顶点B,
顶点C.2.如图三角形ABC 记作:
∠B的对边:
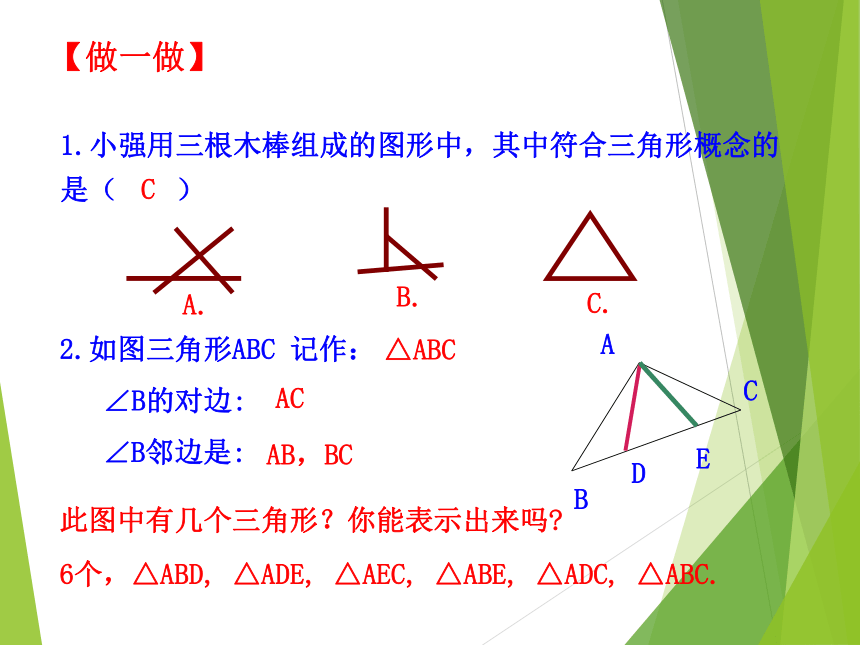
∠B邻边是:1.小强用三根木棒组成的图形中,其中符合三角形概念的
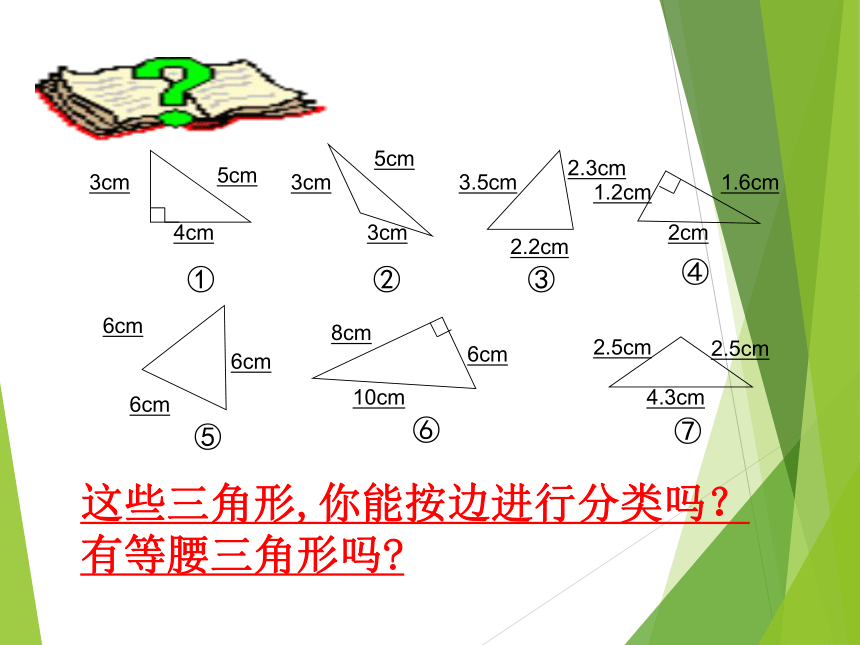
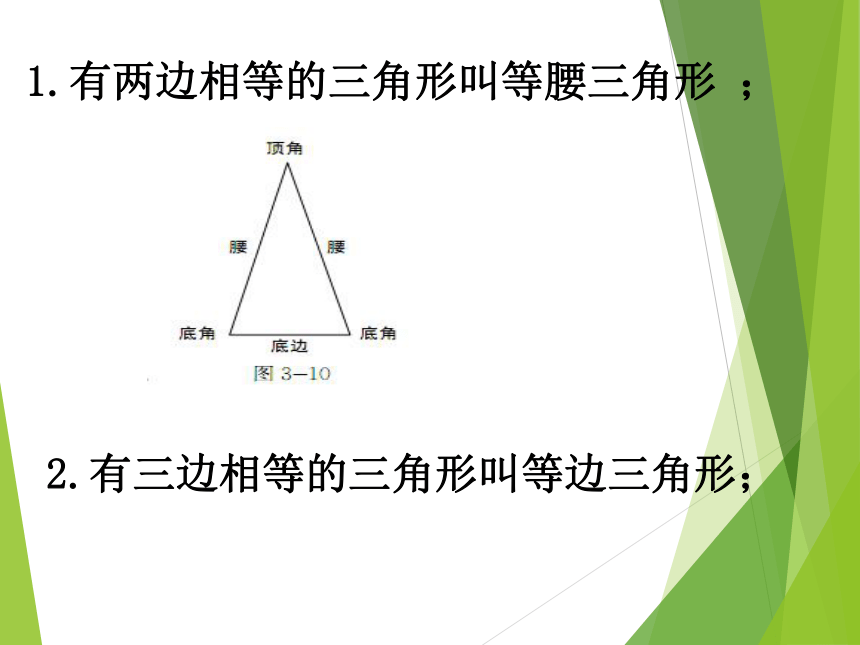
是( )B.此图中有几个三角形?你能表示出来吗?A.C. △ABCACAB,BCDEC6个,△ABD, △ADE, △AEC, △ABE, △ADC, △ABC.【做一做】⑦②①③④⑤⑥这些三角形,你能按边进行分类吗?有等腰三角形吗?3cm4cm5cm3cm3cm5cm2.2cm2.3cm3.5cm6cm6cm6cm8cm6cm10cm4.3cm2.5cm2.5cm1.2cm1.6cm2cm1.有两边相等的三角形叫等腰三角形 ;2.有三边相等的三角形叫等边三角形;三角形按边分: 现有四根纸条,任意取其中三根纸条摆一个三角形,一定能摆成吗? (1)任意画一个△ABC ,量出它的三边长度,并填空:
a=______;b=_______;c=______(2)计算并比较:
a+b____c; b+c____a; c+a____b
(3)通过以上的计算你认为三角形的三边存在怎样的关系?>>> 在A点的小狗,为了尽快吃到B点的香肠,它选择A—B路线,而不选择A—C—B路线,由此你能得到什么结论?CBA三角形任意两边之和大于第三边为什么经常有行人斜穿马路而不走人行横道2.两点之间的所有连线中,线段最短1.三角形任意两边之和大于第三边 计算每个三角形的任意两边之差,并与第三边比较,你能得到什么结论? 分别量出下面三个三角形的三边长度,并填入空格内。a = ,
b = ,
c = 。a = ,
b = ,
c = 。a = ,
b = ,
c = 。任意三角形的两边之差,小于第三边做一做例1:有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?例题解:取长度为2cm的木棒时,由于2+5=7 < 8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形。
取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形。
解题技巧:三角形第三边的取值范围是:
两边之差<第三边<两边之和 下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )不能能能不能 判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?有没有更简便的判断方法? 小窍门: 用较短的两条线段之和与最长的线段比较,若和大,能组成三角形,反之,则不能.例2:若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长。 例题设第三边的长为x,
根据两边之和大于第三边,得:
x<2+7即x<9
根据两边之差小于第三边,得:
x>7-2即x>5
所以x的值大于5小于9,又因为它是奇数,
所以x只能取7。
解: 1.现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度, 要钉成一个三角形木架,应在下列四根木棒中选取 ( )
A.10cm的木棒 B.20cm的木棒 C.50cm的木棒 D.60cm的木棒一、选择题:B 2.已知等腰三角形的两边长分别为3和6,则它的周长为( )
A.9 B.12 C.15 D.12或15 3.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )
A.2cm B.3cm C.4cm D.5cmCBx+x+1+x+2=12 5.若五条线段的长分别是1cm,2cm,3cm,4cm,5cm, 则以其中三条线段为边可构成______个三角形。
二、填空题: 6.若等腰三角形的两边长分别为3和7,则它的周长为_______; 若等腰三角形的两边长分别是3和4,则它的周长为 。 31710或11 等腰三角形在考虑哪条边为腰长时,既要注意有两种情况,还要考虑三角形三边间的关系。(A) 2a-2b (B) 2a+2b+2c
(C) 2b-2c (D) 2a-2c
2019.3.17都有三条边、三个内角 、三个
顶点、三条线段首尾顺次相接.1.这些三角形有什么共同的特点?ABCDEFG由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.什么叫做三角形?3.如何表示三角形?三角形可用符号“△”表示,如图三角形记作:△ABC;读作:三角形ABC.4.三角形的边可以怎样表示?三边可表示为AB,BC,AC,顶点A所对的边BC也可表示为a,顶点B所对的边AC表示为b,顶点C所对的边AB表示为c.【想一想】边:三角形中有三条边:AB,BC,AC.角:三角形中有三个角:∠A,∠B,∠C.顶点:三角形中有三个顶点:顶点A,顶点B,
顶点C.2.如图三角形ABC 记作:
∠B的对边:
∠B邻边是:1.小强用三根木棒组成的图形中,其中符合三角形概念的
是( )B.此图中有几个三角形?你能表示出来吗?A.C. △ABCACAB,BCDEC6个,△ABD, △ADE, △AEC, △ABE, △ADC, △ABC.【做一做】⑦②①③④⑤⑥这些三角形,你能按边进行分类吗?有等腰三角形吗?3cm4cm5cm3cm3cm5cm2.2cm2.3cm3.5cm6cm6cm6cm8cm6cm10cm4.3cm2.5cm2.5cm1.2cm1.6cm2cm1.有两边相等的三角形叫等腰三角形 ;2.有三边相等的三角形叫等边三角形;三角形按边分: 现有四根纸条,任意取其中三根纸条摆一个三角形,一定能摆成吗? (1)任意画一个△ABC ,量出它的三边长度,并填空:
a=______;b=_______;c=______(2)计算并比较:
a+b____c; b+c____a; c+a____b
(3)通过以上的计算你认为三角形的三边存在怎样的关系?>>> 在A点的小狗,为了尽快吃到B点的香肠,它选择A—B路线,而不选择A—C—B路线,由此你能得到什么结论?CBA三角形任意两边之和大于第三边为什么经常有行人斜穿马路而不走人行横道2.两点之间的所有连线中,线段最短1.三角形任意两边之和大于第三边 计算每个三角形的任意两边之差,并与第三边比较,你能得到什么结论? 分别量出下面三个三角形的三边长度,并填入空格内。a = ,
b = ,
c = 。a = ,
b = ,
c = 。a = ,
b = ,
c = 。任意三角形的两边之差,小于第三边做一做例1:有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?例题解:取长度为2cm的木棒时,由于2+5=7 < 8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形。
取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形。
解题技巧:三角形第三边的取值范围是:
两边之差<第三边<两边之和 下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )不能能能不能 判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?有没有更简便的判断方法? 小窍门: 用较短的两条线段之和与最长的线段比较,若和大,能组成三角形,反之,则不能.例2:若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长。 例题设第三边的长为x,
根据两边之和大于第三边,得:
x<2+7即x<9
根据两边之差小于第三边,得:
x>7-2即x>5
所以x的值大于5小于9,又因为它是奇数,
所以x只能取7。
解: 1.现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度, 要钉成一个三角形木架,应在下列四根木棒中选取 ( )
A.10cm的木棒 B.20cm的木棒 C.50cm的木棒 D.60cm的木棒一、选择题:B 2.已知等腰三角形的两边长分别为3和6,则它的周长为( )
A.9 B.12 C.15 D.12或15 3.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )
A.2cm B.3cm C.4cm D.5cmCBx+x+1+x+2=12 5.若五条线段的长分别是1cm,2cm,3cm,4cm,5cm, 则以其中三条线段为边可构成______个三角形。
二、填空题: 6.若等腰三角形的两边长分别为3和7,则它的周长为_______; 若等腰三角形的两边长分别是3和4,则它的周长为 。 31710或11 等腰三角形在考虑哪条边为腰长时,既要注意有两种情况,还要考虑三角形三边间的关系。(A) 2a-2b (B) 2a+2b+2c
(C) 2b-2c (D) 2a-2c
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
