人教版数学七年级下册 8.2 消元——解二元一次方程组(1) 课件(16张PPT)
文档属性
| 名称 | 人教版数学七年级下册 8.2 消元——解二元一次方程组(1) 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 784.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-18 13:04:47 | ||
图片预览





文档简介
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡儿[Descartes, 1596-1650 ]
8.2 消元—解二元一次方程组
第1课时
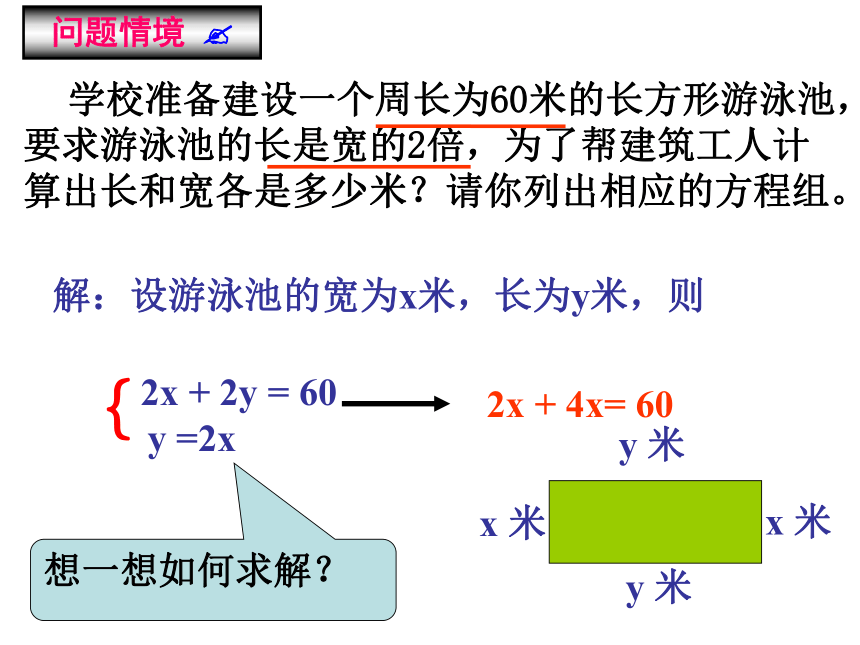
学校准备建设一个周长为60米的长方形游泳池,要求游泳池的长是宽的2倍,为了帮建筑工人计算出长和宽各是多少米?请你列出相应的方程组。
解:设游泳池的宽为x米,长为y米,则
2x + 2y = 60
{
y =2x
问题情境 ?
想一想如何求解?
2x + 4x= 60
上面的解方程组的基本思路是什么?基本步骤有哪些?
上面解方程组的基本思路是把“二元”转化为“一元” —— “消元”
主要步骤是:将含一个未知数表示另一个未知数的代数式,代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。这种解方程组的方法称为代入消元法,简称代入法。
归纳 ?
将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
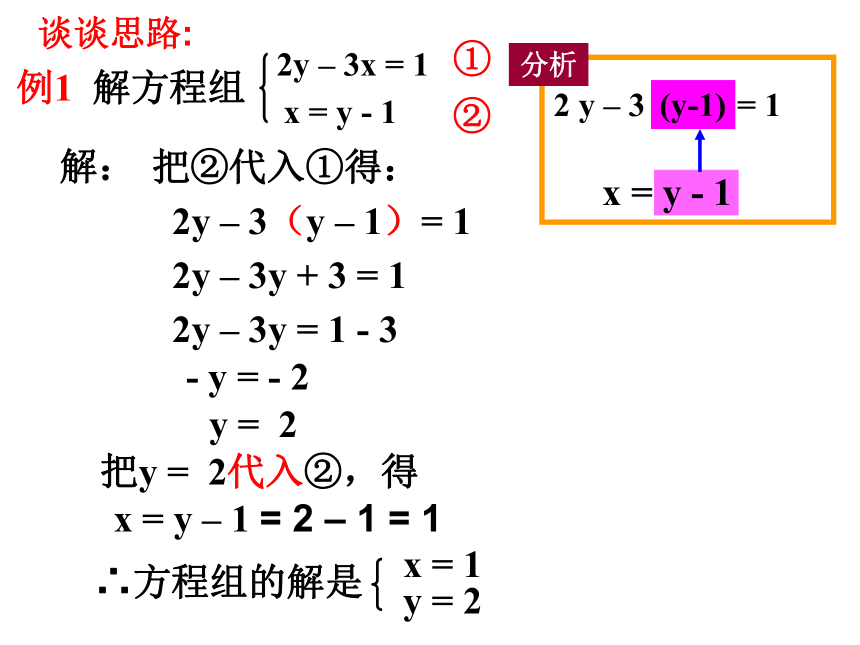
解:
①
②
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
2 y – 3 x = 1
x = y - 1
(y-1)
谈谈思路:
①
②
谈谈思路:
解:
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
例2 解方程组
解:
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
变
代
求
写
9+3y– 8y= 14
– 5y= 5
y= – 1
说说方法:
1、二元一次方程组
这节课我们学习了什么知识?
代入消元法
一元一次方程
2、代入消元法的一般步骤:
3、思想方法:转化思想、消元思想、
方程(组)思想.
变
代
求
写
1
转化
解二元一次方程组
(1)
(2)
(3)
(4)
1、用代入法解二元一次方程组
(1)
(2)
2 . 已知 是二元一次方程组
的解,则 a= ,b= 。
3.已知 (a+2b-5)2+|4a+b-6|=0, 求a和b的值.
3
1
4、已知钢笔每只5元,圆珠笔每只2元,小明用16元钱买了这两种笔共5支,试求小明买钢笔和圆珠笔各多少支?
解:设小明买钢笔x支,买圆珠笔y支,根据题意列出方程组得
x+y=5
5x+2y=16
解得:
x=2
y=3
答:小明买钢笔2支,买圆珠笔3支.
5、如图所示,将长方形ABCD的一个角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD的度数分别为x ,y度,那么x,y所适合的一个方程组是( )
A
B
C
D
C
17.5探索与实践
小组竞赛
设甲数为x,乙数为y,根据下列语句,列二元一次方程.
(1)甲数的3倍比乙数大5;
(2)甲数比乙数的2倍少2;
(3)甲数的2倍与乙数的3倍的和是20;
(4)甲乙两数之差为2.
3x-y=5
x=2y-2
2x+3y=20
x-y=2
17.5探索与实践
(1)甲数的3倍比乙数大5;
(2)甲数比乙数的2倍少2;
(3)甲数的2倍与乙数的3倍的和是20;
(4)甲乙两数之差为2.
x-y=2
2x+3y=20
x=2y-2
3x-y=5
小组竞赛
练习:93页第1、2题
——法国数学家 笛卡儿[Descartes, 1596-1650 ]
8.2 消元—解二元一次方程组
第1课时
学校准备建设一个周长为60米的长方形游泳池,要求游泳池的长是宽的2倍,为了帮建筑工人计算出长和宽各是多少米?请你列出相应的方程组。
解:设游泳池的宽为x米,长为y米,则
2x + 2y = 60
{
y =2x
问题情境 ?
想一想如何求解?
2x + 4x= 60
上面的解方程组的基本思路是什么?基本步骤有哪些?
上面解方程组的基本思路是把“二元”转化为“一元” —— “消元”
主要步骤是:将含一个未知数表示另一个未知数的代数式,代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。这种解方程组的方法称为代入消元法,简称代入法。
归纳 ?
将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
解:
①
②
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
2 y – 3 x = 1
x = y - 1
(y-1)
谈谈思路:
①
②
谈谈思路:
解:
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
例2 解方程组
解:
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
变
代
求
写
9+3y– 8y= 14
– 5y= 5
y= – 1
说说方法:
1、二元一次方程组
这节课我们学习了什么知识?
代入消元法
一元一次方程
2、代入消元法的一般步骤:
3、思想方法:转化思想、消元思想、
方程(组)思想.
变
代
求
写
1
转化
解二元一次方程组
(1)
(2)
(3)
(4)
1、用代入法解二元一次方程组
(1)
(2)
2 . 已知 是二元一次方程组
的解,则 a= ,b= 。
3.已知 (a+2b-5)2+|4a+b-6|=0, 求a和b的值.
3
1
4、已知钢笔每只5元,圆珠笔每只2元,小明用16元钱买了这两种笔共5支,试求小明买钢笔和圆珠笔各多少支?
解:设小明买钢笔x支,买圆珠笔y支,根据题意列出方程组得
x+y=5
5x+2y=16
解得:
x=2
y=3
答:小明买钢笔2支,买圆珠笔3支.
5、如图所示,将长方形ABCD的一个角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD的度数分别为x ,y度,那么x,y所适合的一个方程组是( )
A
B
C
D
C
17.5探索与实践
小组竞赛
设甲数为x,乙数为y,根据下列语句,列二元一次方程.
(1)甲数的3倍比乙数大5;
(2)甲数比乙数的2倍少2;
(3)甲数的2倍与乙数的3倍的和是20;
(4)甲乙两数之差为2.
3x-y=5
x=2y-2
2x+3y=20
x-y=2
17.5探索与实践
(1)甲数的3倍比乙数大5;
(2)甲数比乙数的2倍少2;
(3)甲数的2倍与乙数的3倍的和是20;
(4)甲乙两数之差为2.
x-y=2
2x+3y=20
x=2y-2
3x-y=5
小组竞赛
练习:93页第1、2题
