19.3.3菱形的性质与判定 同步练习
图片预览


文档简介
19.3.3菱形的性质与判定 同步练习
一.选择题
1. 菱形具有而平行四边形不一定具有的性质是( )
A. 对角线互相垂直 B. 对角线相等
C. 对角线互相平分 D. 对角相等
2. 若菱形的两条对角线分别为8, 6,则菱形的面积为,( )
A. 48 B.24 C.14 D.12
3. 如图,菱形ABCD的周长为28,对角线AC、BD交于点O,E为AD的中点,则OA的长等于( )
A.2 B.3.5 C.7 D.14
4. 如图,丝带重叠的部分一定是( )
A. 正方形 B. 矩形 C.菱形 D. 都有可能
5. 如图要判定□ABCD是菱形,需要添加的条件是( )
A. AB=AC B. BC=BD C.AC=BD D. AB=BC
二.填空题
1. 如图已知菱形ABCD的边长是10,点O是对角线的交点,过点O的三条直线将菱形分成阴影和空白部分,若菱形一条对角线长12,则图中阴影部分的面积为 .
2. 如图,在菱形OA BC中,点B在x轴上,点A的坐标为(3,5),则点C的坐标为 .
3. 如图,小明在做线段AB的垂直平分线时,操作如下: 分别以A和B为圆心,大于AB的长为半径画弧,两弧相交于CD,则直线CD即为所求,根据它的作图方法可知四边形ADBC一定是 .
4. 如图等边三角形ABC中,D、E、F分别是AB 、BC、CA边上的中点这图中有 个菱形.
三.解答题
1. 如图在菱形ABCD中,点E、F分别在BC和CD上且CE=CF连接AE、AF,求证:∠BAE=∠DAF.
2. 如图,∠ABC=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点,
(1)证明:四边形CFAE是菱形,
(2)连接EF交AC于点O,若BC=,求线段OF的长.
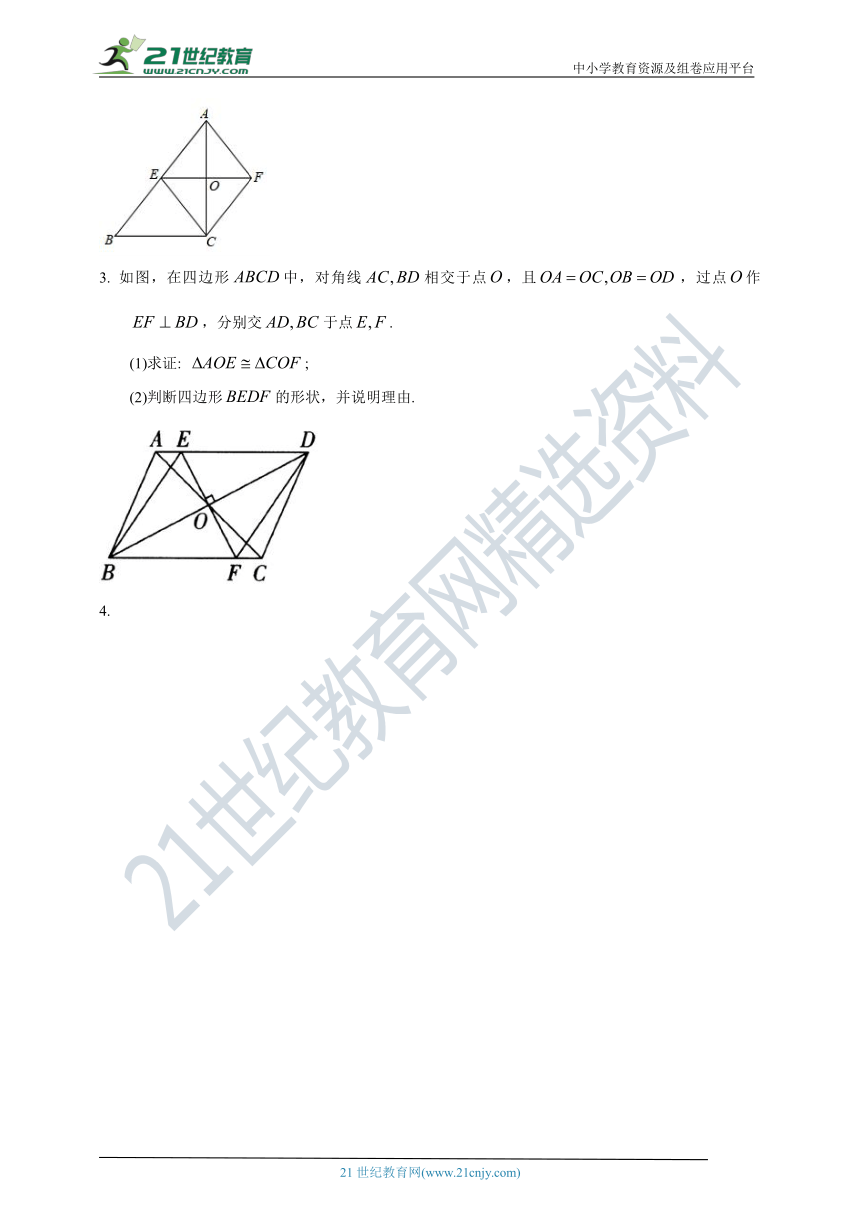
3. 如图,在四边形中,对角线相交于点,且,过点作,分别交于点.
(1)求证: ;
(2)判断四边形的形状,并说明理由.
4.
参考答案
一.1.A 2.B 3.B 4.C 5.D
二.1.48
2.(3,-5)
3. 菱形
4.3
三
∵四边形ABCD是菱形,
∴AB=AD=BC=CD, ∠B=∠D
∵CE=CF
∴BE=DF
在△ABO和△DCO中,
AB=AD,∠B=∠D, BE=DF,
∴△ABE≌△ADF
∴∠BAE=∠DAF
(1)证明:∵∠ABC=90°,点E是AB边的中点,
∴22CE=AB=2EA
∵点F恰是点E关于AC所在直线的对称点,
∴AE=AF,CE=CF
∴CE=EA=AF=CF
∴四边形CFAE是菱形,
(2) ∵四边形CFAE是菱形,
∴OA=OC,CE=CF
∴
∴.
3. (1)∵OA=OC、OB=OD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA,
又∵∠AOE=∠COF,OA=OC,
∴△AOE≌△COF(ASA);
(2)四边形BEDF是菱形,理由如下:
∵△AOE≌△COF,
∴OE=OF,
又∵OB=OD,
∴四边形DEBF是平行四边形,
又∵EF⊥BD,
∴平行四边形DEBF是菱形.
一.选择题
1. 菱形具有而平行四边形不一定具有的性质是( )
A. 对角线互相垂直 B. 对角线相等
C. 对角线互相平分 D. 对角相等
2. 若菱形的两条对角线分别为8, 6,则菱形的面积为,( )
A. 48 B.24 C.14 D.12
3. 如图,菱形ABCD的周长为28,对角线AC、BD交于点O,E为AD的中点,则OA的长等于( )
A.2 B.3.5 C.7 D.14
4. 如图,丝带重叠的部分一定是( )
A. 正方形 B. 矩形 C.菱形 D. 都有可能
5. 如图要判定□ABCD是菱形,需要添加的条件是( )
A. AB=AC B. BC=BD C.AC=BD D. AB=BC
二.填空题
1. 如图已知菱形ABCD的边长是10,点O是对角线的交点,过点O的三条直线将菱形分成阴影和空白部分,若菱形一条对角线长12,则图中阴影部分的面积为 .
2. 如图,在菱形OA BC中,点B在x轴上,点A的坐标为(3,5),则点C的坐标为 .
3. 如图,小明在做线段AB的垂直平分线时,操作如下: 分别以A和B为圆心,大于AB的长为半径画弧,两弧相交于CD,则直线CD即为所求,根据它的作图方法可知四边形ADBC一定是 .
4. 如图等边三角形ABC中,D、E、F分别是AB 、BC、CA边上的中点这图中有 个菱形.
三.解答题
1. 如图在菱形ABCD中,点E、F分别在BC和CD上且CE=CF连接AE、AF,求证:∠BAE=∠DAF.
2. 如图,∠ABC=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点,
(1)证明:四边形CFAE是菱形,
(2)连接EF交AC于点O,若BC=,求线段OF的长.
3. 如图,在四边形中,对角线相交于点,且,过点作,分别交于点.
(1)求证: ;
(2)判断四边形的形状,并说明理由.
4.
参考答案
一.1.A 2.B 3.B 4.C 5.D
二.1.48
2.(3,-5)
3. 菱形
4.3
三
∵四边形ABCD是菱形,
∴AB=AD=BC=CD, ∠B=∠D
∵CE=CF
∴BE=DF
在△ABO和△DCO中,
AB=AD,∠B=∠D, BE=DF,
∴△ABE≌△ADF
∴∠BAE=∠DAF
(1)证明:∵∠ABC=90°,点E是AB边的中点,
∴22CE=AB=2EA
∵点F恰是点E关于AC所在直线的对称点,
∴AE=AF,CE=CF
∴CE=EA=AF=CF
∴四边形CFAE是菱形,
(2) ∵四边形CFAE是菱形,
∴OA=OC,CE=CF
∴
∴.
3. (1)∵OA=OC、OB=OD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA,
又∵∠AOE=∠COF,OA=OC,
∴△AOE≌△COF(ASA);
(2)四边形BEDF是菱形,理由如下:
∵△AOE≌△COF,
∴OE=OF,
又∵OB=OD,
∴四边形DEBF是平行四边形,
又∵EF⊥BD,
∴平行四边形DEBF是菱形.
