【华师大版八年级下册进阶培优训练】第十讲 平行四边形的性质和判定培优辅导(含答案)
文档属性
| 名称 | 【华师大版八年级下册进阶培优训练】第十讲 平行四边形的性质和判定培优辅导(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-18 19:46:45 | ||
图片预览



文档简介
第十讲 平行四边形的性质和判定培优辅导
一、知识梳理
1.平行四边形:
(1)平行四边形的定义:两组对边 的四边形是平行四边形.
平行四边形用符号 表示.平行四边形ABCD记作 ,读作平行四边形ABCD.
平行四边形的性质:平行四边形是 对称图形,对称中心是 。
(1)边: 。 (2)角: 。
(3)对角线: 。
(4)若一条直线过平行四边形两对角线的交点,则这直线被一组对边截下的线段以对角线的交点为中点,且这条直线 等分平行四边形的面积.
3.两条平行线间的距离:
(1)定义:两条平行线中, ,叫做这两条平行线间的距离.
(2)两平行线间的距离 .
4.平行四边形的面积:(1)如图①,.
(2)同底(等底)同高(等高)的平行四边形面积相等.
如图②,有公共边BC,则.
平行四边形的两条对角线把平行四边形分成四个面积相等的小三角形,如图有
5.平行四边形的判别方法:
平行四边形的判定的方法有从边的条件有:①两组对边__________的四边形是平行四边形;
②两组对边__________的四边形是平行四边形;③一组对边__________的四边形是平行四边形.
从对角线的条件有:④两条对角线__________的四边形是平行四边形.
从角的条件有:⑤两组对角__________的四边形是平行四边形.
注意:一组对边平行另一组对边相等的四边形__________是平行四边形。
6.平行四边形知识的运用:
(1)直接运用平行四边形特征解决某些问题,如求角的度数,线段的长度,证明角相等或互补,证明线段相等或倍分等.
(2)识别一个四边形为平行四边形,从而得到两直线平行.
(3)先识别—个四边形是平行四边形,然后再用平行四边形的特征去解决某些问题.
二、重点突破(一)平行四边形的性质
1、□ABCD的周长为60cm,其对角线交于O点,若△AOB的周长比△BOC的周长多10cm,则AB=_ _,BC= .
2、□ABCD中,对角线AC和BD交于O,若AC=8,BD=6,则边AB长的取值范围是 。
3、平行四边形周长是40cm,则每条对角线长不能超过 cm.
4、以不共线三点A、B、C为顶点的平行四边形共有______个.
5、如图,在□ABCD中,AE、AF分别垂直于BC、CD,垂足为E、F,若∠EAF=30°,AB=6,AD=10,则CD=_____;AB与CD的距离为______;AD与BC的距离为_____;∠D=______.
6、如图6,在平行四边形ABCD中,DB=DC、,CEBD于E,则 .
第6题图 第7题图 第8题图 第9题图
7、在平行四边形ABCD中,点A1、A2、A3、A4和C1、C2、C3、C4分别AB和CD的五等分点,点B1、B2和D1、D2分别是BC和DA的三等分点,已知四边形A4 B2 C4 D2的面积为1,则平行四边形ABCD面积为 .
8、已知平分,,,则 .
9、如图,平行四边形的周长为20cm ,AE⊥BC于E,AF⊥CD于F,AE=2 cm,AF=3 cm,求平行四边形ABCD的面积 .
10、如图,△ABC是边长为1的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB交AC、BC于点E、F,作GH∥BC交AB、AC于点G、H,作MN∥AC交AB、BC于M、N,请你猜想EF+GH+MN的值是多少?其值是否随点P位置的改变而变化?并证明你的结论.
(二)平行四边形的判定
★1.两组对边分别平行的四边形为平行四边形
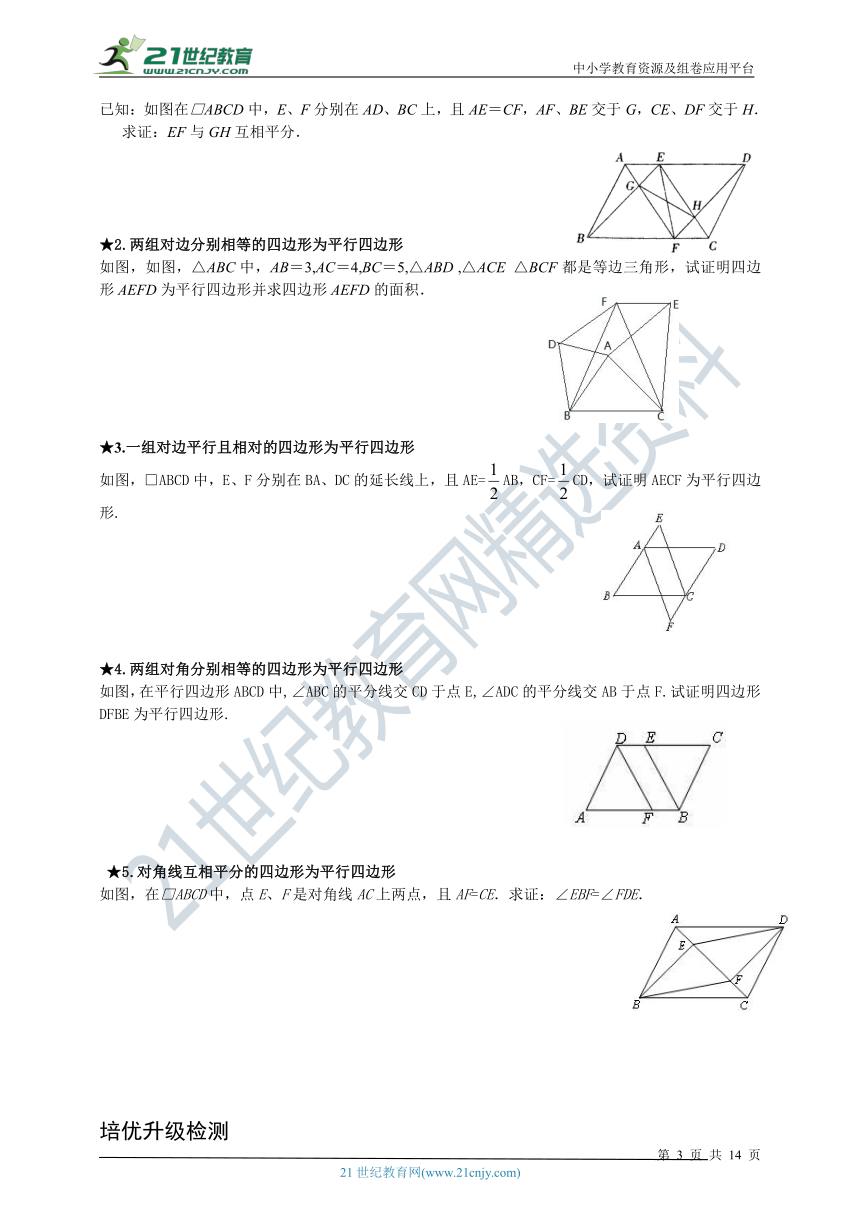
已知:如图在□ABCD中,E、F分别在AD、BC上,且AE=CF,AF、BE交于G,CE、DF交于H.
求证:EF与GH互相平分.
★2.两组对边分别相等的四边形为平行四边形
如图,如图,△ABC中,AB=3,AC=4,BC=5,△ABD ,△ACE △BCF都是等边三角形,试证明四边形AEFD为平行四边形并求四边形AEFD的面积.
★3.一组对边平行且相对的四边形为平行四边形
如图,□ABCD中,E、F分别在BA、DC的延长线上,且AE=AB,CF=CD,试证明AECF为平行四边形.
★4.两组对角分别相等的四边形为平行四边形
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试证明四边形DFBE为平行四边形.
★5.对角线互相平分的四边形为平行四边形
如图,在□ABCD中,点E、F是对角线AC上两点,且AF=CE.求证:∠EBF=∠FDE.
培优升级检测
1、(成都)已知四边形ABCD,有以下四个条件: (AB∥CD (AB=CD (BC∥AD ④BC=AD 从这四个条件中任选两个,能使四边形ABCD为平行四边形的选法种数有( )
A.6种 B.5种 C.4种 D.3种
2、某广场有一个形状是平行四边形的花坛(如图)分别种有红黄蓝绿橙紫6得颜色的花,如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法错误的是( )
A.红花,绿花种植面积一定相等 B.紫花,橙花种植面积一定相等
C.红花,蓝花种植面积一定相等 D.蓝花,黄花种植面积一定相等
3、(陕西)如图,l1 ∥ l2 BE∥CF, BA⊥l1 DC ⊥l2,下面四个结论中(AB=DC; (BE=CF (S△ADE=S△DCF ④S□ABCD=S□BCFE,其中正确的有( )
A.4个 B .3个 C.2个 D .1个
4、、如图□ABCD中,BC=2AB,CE⊥AB,E为垂足,F为AD的中点,若∠AEF=54°,求∠B的度数.
5、如图,在直角坐标系中,A(0,1),B(0,3),P是x轴上一动点,在直线y=x上是否存在点Q,使以A、B、P、Q为顶点的四边形为平行四边形?若存在,画出所有满足情况的平行四边形,并求出对应的P、Q的坐标;若不存在,请说明理由.
6、在课外小组活动时,小慧拿来一道题和小东,小明交流.
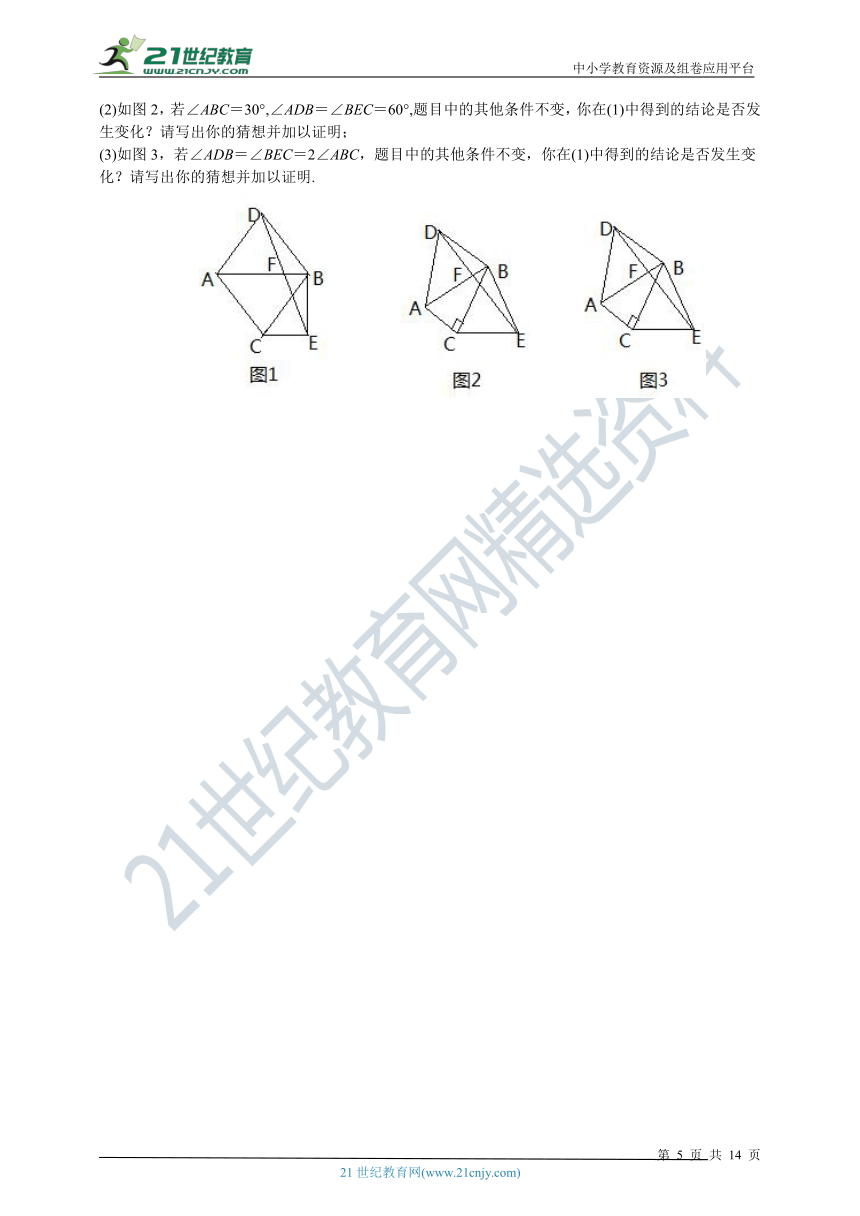
题目:如图1,已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB,BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F,探究线段DF与EF的数量关系.
小慧同学的思路是:过点D作DG⊥AB于点G,构造全等三角形,通过推理使问题得解.
小东同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.
小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.
请你参考小慧同学的思路,探究并解决这三位同学提出的问题:
(1)写出题目中DF与EF的数量关系;
(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,题目中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;
(3)如图3,若∠ADB=∠BEC=2∠ABC,题目中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.
第十讲 平行四边形的性质和判定培优辅导答案
一、知识梳理
1.平行四边形:
(1)平行四边形的定义:两组对边 分别平行 的四边形是平行四边形.
平行四边形用符号 ∥ 表示.平行四边形ABCD记作 □ABCD ,读作平行四边形ABCD.
2.平行四边形的性质:平行四边形是 中心 对称图形,对称中心是 两条对角线的交点
(1)边: 平行四边形的对边平行且相等. 。 (2)角: 平行四边形的对角相等,邻角互补 。
(3)对角线: 平行四边形的对角线互相平分 。
(4)若一条直线过平行四边形两对角线的交点,则这直线被一组对边截下的线段以对角线的交点为中点,且这条直线 二等分 等分平行四边形的面积.
3.两条平行线间的距离:
(1)定义:两条平行线中, 一条直线上的任意一点到另一条直线的距离 ,叫做这两条平行线间的距离.
(2)两平行线间的距离 处处相等 .
4.平行四边形的面积:(1)如图①,.
(2)同底(等底)同高(等高)的平行四边形面积相等.
如图②,有公共边BC,则.
平行四边形的两条对角线把平行四边形分成四个面积相等的小三角形,如图有
5.平行四边形的判别方法:
平行四边形的判定的方法有从边的条件有:①两组对边_分别平行_________的四边形是平行四边形;
②两组对边__分别相等________的四边形是平行四边形;③一组对边_平行且相等___的四边形是平行四边形.
从对角线的条件有:④两条对角线__互相平分________的四边形是平行四边形.
从角的条件有:⑤两组对角___分别相等_______的四边形是平行四边形.
注意:一组对边平行另一组对边相等的四边形_____不是_____是平行四边形。
6.平行四边形知识的运用:
(1)直接运用平行四边形特征解决某些问题,如求角的度数,线段的长度,证明角相等或互补,证明线段相等或倍分等.
(2)识别一个四边形为平行四边形,从而得到两直线平行.
(3)先识别—个四边形是平行四边形,然后再用平行四边形的特征去解决某些问题.
二、重点突破
(一)平行四边形的性质
1、□ABCD的周长为60cm,其对角线交于O点,若△AOB的周长比△BOC的周长多10cm,则AB=_30__,BC=___10_____.
2、□ABCD中,对角线AC和BD交于O,若AC=8,BD=6,则边AB长的取值范围是_13、平行四边形周长是40cm,则每条对角线长不能超过___20____cm.
4、以不共线三点A、B、C为顶点的平行四边形共有___C____个.
5、如图,在□ABCD中,AE、AF分别垂直于BC、CD,垂足为E、F,若∠EAF=30°,AB=6,AD=10,则CD=_____6_____;AB与CD的距离为_____5_____;AD与BC的距离为___3_______;∠D=_____30°_____.
6、如图6,在平行四边形ABCD中,DB=DC、,CEBD于E,则 25° .
第6题图 第7题图 第8题图 第9题图
7、在平行四边形ABCD中,点A1、A2、A3、A4和C1、C2、C3、C4分别AB和CD的五等分点,点B1、B2和D1、D2分别是BC和DA的三等分点,已知四边形A4 B2 C4 D2的面积为1,则平行四边形ABCD面积为 .
8、已知平分,,,则 3 .
9、如图,平行四边形的周长为20cm ,AE⊥BC于E,AF⊥CD于F,AE=2 cm,AF=3 cm,求平行四边形ABCD的面积 12cm2 .
10、如图,△ABC是边长为1的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB交AC、BC于点E、F,作GH∥BC交AB、AC于点G、H,作MN∥AC交AB、BC于M、N,请你猜想EF+GH+MN的值是多少?其值是否随点P位置的改变而变化?并证明你的结论.
解:EF+GH+MN=8,其值不会随点P位置的改变而变化,理由如下:
∵MN∥AC,EF∥AB, ∴四边形AMPE是平行四边形, ∴PE=AM.同理PF=GB.∴EF=PE+PF=AM+GB ① ∵△ABC是等边三角形∴∠A=∠B=∠C=60° ∵GH∥BC∴∠AGH=∠B=60°,∠AHG=∠C=60° ∴△AGH是等边三角形 ∴GH=AG=AM+MG ② 同理MN=MB=MG+GB ③ ①+②+③得 EF+GH+MN=AM+GB+AM+MG+MG+GB=2(AM+MG+GB)=2AB=2x4=8 即EF+GH+MN=2AB=8.
(二)平行四边形的判定
★1.两组对边分别平行的四边形为平行四边形
已知:如图在□ABCD中,E、F分别在AD、BC上,且AE=CF,AF、BE交于G,CE、DF交于H.
求证:EF与GH互相平分.
解答 证明:∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC, ∴AE∥FC, ∵AE=FC, ∴四边形AFCE是平行四边形, ∴AF∥EC, ∵AD=BC,AE=FC, ∴ED=BF, ∵ED∥BF, ∴四边形EBFD是平行四边形, ∴∠EBF=∠EDF, ∵AF∥EC,AD∥BC, ∴∠AFB=∠ECB,∠ECB=∠CED, ∴∠AFB=∠CED, 在△BGF和△DHE中, ∴△BGF≌△HED(ASA), ∴GF=EH, ∴四边形EGFH是平行四边形.
∴EF与GH互相平分
★2.两组对边分别相等的四边形为平行四边形
如图,如图,△ABC中,AB=3,AC=4,BC=5,△ABD ,△ACE △BCF都是等边三角形,试证明四边形AEFD为平行四边形并求四边形AEFD的面积.
解:如图,△ABC中,AB=3,AC=4,BC=5, ∴BC2=AB2+AC2, ∴∠BAC=90°, ∵△ABD,△ACE都是等边三角形, ∴∠DAB=∠EAC=60°, ∴∠DAE=150°. ∵△ABD和△FBC都是等边三角形, ∴∠DBF+∠FBA=∠ABC+∠ABF=60°, ∴∠DBF=∠ABC. 在△ABC与△DBF中,
∴△ABC≌△DBF(SAS), ∴AC=DF=AE=4, 同理可证△ABC≌△EFC, ∴AB=EF=AD=3, ∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形). ∴∠FDA=180°-∠DAE=30°, ∴S?AEFD==3×(4×)=6. 答:四边形AEFD的面积是6.
★3.一组对边平行且相对的四边形为平行四边形
如图,□ABCD中,E、F分别在BA、DC的延长线上,且AE=AB,CF=CD,试证明AECF为平行四边形.
证明:∵四边形ABCD是平行四边形, ∴AB∥CD,AB=CD, ∵AE=AB,CF=CD
∵AE=CF
又∵AE∥CF
∴AECF为平行四边形.
★4.两组对角分别相等的四边形为平行四边形
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试证明四边形DFBE为平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,∠ADC=∠ABC
∵∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F
∴∠ADF=∠CDF=∠ADC,∠CBE=∠ABE=∠ABC,
∴∠ADF=∠CDF=∠CBE=∠ABE,
∵∠DFB=∠ADF+∠A ∠DEB=∠EBC+∠C
∴∠DFB=∠DEB且∠ABE=∠CDF
∴四边形DFBE为平行四边形.
★5.对角线互相平分的四边形为平行四边形
如图,在□ABCD中,点E、F是对角线AC上两点,且AF=CE.求证:∠EBF=∠FDE.
证明:连接BD交AC于O点, ∵四边形ABCD是平行四边形, ∴OA=OC,OB=OD, 又∵AE=CF, ∴OE=OF, ∴四边形BEDF是平行四边形, ∴∠EBF=∠EDF。
培优升级检测
1、(成都)已知四边形ABCD,有以下四个条件: (AB∥CD (AB=CD (BC∥AD ④BC=AD 从这四个条件中任选两个,能使四边形ABCD为平行四边形的选法种数有( C )
A.6种 B.5种 C.4种 D.3种
2、某广场有一个形状是平行四边形的花坛(如图)分别种有红黄蓝绿橙紫6得颜色的花,如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法错误的是( C )
A.红花,绿花种植面积一定相等 B.紫花,橙花种植面积一定相等
C.红花,蓝花种植面积一定相等 D.蓝花,黄花种植面积一定相等
3、(陕西)如图,l1 ∥ l2 BE∥CF, BA⊥l1 DC ⊥l2,下面四个结论中(AB=DC; (BE=CF (S△ADE=S△DCF ④S□ABCD=S□BCFE,其中正确的有( A )
A.4个 B .3个 C.2个 D .1个
4、、如图□ABCD中,BC=2AB,CE⊥AB,E为垂足,F为AD的中点,若∠AEF=54°,求∠B的度数.
解:延长EF与CD的延长线交于点G,连接CF,如图所示, ∵平行四边形ABCD, ∴CD∥AB,DC=AB,BC=AD, ∴∠AEF=∠G, ∵F为AD的中点,∴AF=DF, 又∠AFE=∠DFG, ∴△AEF≌△GDF(AAS), ∴FG=FE,∠G=∠AEF=54°, ∵CE⊥AB,CD∥AB, ∴EC⊥DC,即∠GCE=90°, 在Rt△CGE中,可得CF=GF=EF=GE,
∴∠FCG=∠G=54°, 又BC=AD=2AB=2DC,F为AD中点, ∴CD=FD, ∴∠DCF=∠CFD=54°, ∴∠B=∠CDA=180°-54°-54°=72°.
5、如图,在直角坐标系中,A(0,1),B(0,3),P是x轴上一动点,在直线y=x上是否存在点Q,使以A、B、P、Q为顶点的四边形为平行四边形?若存在,画出所有满足情况的平行四边形,并求出对应的P、Q的坐标;若不存在,请说明理由.
解:如1,∵P是x轴上一动点,点Q在直线y=x上,
∴设P(x,0),Q(a,a),
当AB是平行四边形的边时,
∵AB=3-1=2,∴PQ=AB=2,∴a=±2,
∴P1(-2,0),Q1(-2,-2)或P2(2,0),Q2(2,2);
如图2,当AB是平行四边形的对角线时,
BQ=AP是a2+(a-3)2=x2+12,即2a2-6a=x2-8①;
PB=AQ是a2+(a-1)2=32+x2,即2a2-2a=x2-9②.
①-②得a=4,把a=4代入①得,17=1+x2,
解得x=±4,
∴P3(-4,0),Q3(4,4)或P4(4,0),Q4(4,4)(舍去).
6、在课外小组活动时,小慧拿来一道题和小东,小明交流.
题目:如图1,已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB,BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F,探究线段DF与EF的数量关系.
小慧同学的思路是:过点D作DG⊥AB于点G,构造全等三角形,通过推理使问题得解.
小东同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.
小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.
请你参考小慧同学的思路,探究并解决这三位同学提出的问题:
(1)写出题目中DF与EF的数量关系;
(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,题目中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;
(3)如图3,若∠ADB=∠BEC=2∠ABC,题目中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.
解:(1)DF=EF;
(2)猜想:DF=FE; 证明:如图(1)所示,过点D作DG⊥AB于G,则∠DGB=90° ∵DA=DB,∠ADB=60°, ∴AG=BC,△DBA是等边三角形, ∴DB=BA, ∵∠ACB=90°,∠ABC=30° ∴AC=1/2AB=BG, ∴△DBG≌△BAC, ∴DG=BC, ∵BE=EC,∠BEC=60°, ∴△EBC是等边三角形, ∴BC=BE,∠CBE=60°, ∴DG=BE,∠ABE=∠ABC+∠CBE=90°, ∵∠DFC=∠EFB,∠DCF=∠EBF, ∴△DFC≌△EFB, ∴DF=EF;
(3)猜想:DF=FE; 如图(2)所示,过点D作DH⊥AB于H,连接HC,HE,HE交CB于K,则∠DHB=90°, ∵DA=DB, ∴AH=BH,∠1=∠HDB, ∵∠ACB=90°, ∴HC=HB, ∵EB=EC,HE=HE, ∴△HBE≌△HCE, ∴∠2=∠3,∠4=∠BEH, ∴HK⊥BC, ∴∠BKE=90°, ∵∠ADB=∠BEC=2∠ABC, ∴∠HDB=∠BEH=∠ABC, ∴∠DBC=∠DBH+∠ABC=∠DBH+∠HDB=90°, ∠EBH=∠EBK+∠ABC=∠EBK+∠BEK=90°, ∴DB∥HE,DH∥BE, ∴四边形DHEB是平行四边形, ∴BF=EF。
一、知识梳理
1.平行四边形:
(1)平行四边形的定义:两组对边 的四边形是平行四边形.
平行四边形用符号 表示.平行四边形ABCD记作 ,读作平行四边形ABCD.
平行四边形的性质:平行四边形是 对称图形,对称中心是 。
(1)边: 。 (2)角: 。
(3)对角线: 。
(4)若一条直线过平行四边形两对角线的交点,则这直线被一组对边截下的线段以对角线的交点为中点,且这条直线 等分平行四边形的面积.
3.两条平行线间的距离:
(1)定义:两条平行线中, ,叫做这两条平行线间的距离.
(2)两平行线间的距离 .
4.平行四边形的面积:(1)如图①,.
(2)同底(等底)同高(等高)的平行四边形面积相等.
如图②,有公共边BC,则.
平行四边形的两条对角线把平行四边形分成四个面积相等的小三角形,如图有
5.平行四边形的判别方法:
平行四边形的判定的方法有从边的条件有:①两组对边__________的四边形是平行四边形;
②两组对边__________的四边形是平行四边形;③一组对边__________的四边形是平行四边形.
从对角线的条件有:④两条对角线__________的四边形是平行四边形.
从角的条件有:⑤两组对角__________的四边形是平行四边形.
注意:一组对边平行另一组对边相等的四边形__________是平行四边形。
6.平行四边形知识的运用:
(1)直接运用平行四边形特征解决某些问题,如求角的度数,线段的长度,证明角相等或互补,证明线段相等或倍分等.
(2)识别一个四边形为平行四边形,从而得到两直线平行.
(3)先识别—个四边形是平行四边形,然后再用平行四边形的特征去解决某些问题.
二、重点突破(一)平行四边形的性质
1、□ABCD的周长为60cm,其对角线交于O点,若△AOB的周长比△BOC的周长多10cm,则AB=_ _,BC= .
2、□ABCD中,对角线AC和BD交于O,若AC=8,BD=6,则边AB长的取值范围是 。
3、平行四边形周长是40cm,则每条对角线长不能超过 cm.
4、以不共线三点A、B、C为顶点的平行四边形共有______个.
5、如图,在□ABCD中,AE、AF分别垂直于BC、CD,垂足为E、F,若∠EAF=30°,AB=6,AD=10,则CD=_____;AB与CD的距离为______;AD与BC的距离为_____;∠D=______.
6、如图6,在平行四边形ABCD中,DB=DC、,CEBD于E,则 .
第6题图 第7题图 第8题图 第9题图
7、在平行四边形ABCD中,点A1、A2、A3、A4和C1、C2、C3、C4分别AB和CD的五等分点,点B1、B2和D1、D2分别是BC和DA的三等分点,已知四边形A4 B2 C4 D2的面积为1,则平行四边形ABCD面积为 .
8、已知平分,,,则 .
9、如图,平行四边形的周长为20cm ,AE⊥BC于E,AF⊥CD于F,AE=2 cm,AF=3 cm,求平行四边形ABCD的面积 .
10、如图,△ABC是边长为1的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB交AC、BC于点E、F,作GH∥BC交AB、AC于点G、H,作MN∥AC交AB、BC于M、N,请你猜想EF+GH+MN的值是多少?其值是否随点P位置的改变而变化?并证明你的结论.
(二)平行四边形的判定
★1.两组对边分别平行的四边形为平行四边形
已知:如图在□ABCD中,E、F分别在AD、BC上,且AE=CF,AF、BE交于G,CE、DF交于H.
求证:EF与GH互相平分.
★2.两组对边分别相等的四边形为平行四边形
如图,如图,△ABC中,AB=3,AC=4,BC=5,△ABD ,△ACE △BCF都是等边三角形,试证明四边形AEFD为平行四边形并求四边形AEFD的面积.
★3.一组对边平行且相对的四边形为平行四边形
如图,□ABCD中,E、F分别在BA、DC的延长线上,且AE=AB,CF=CD,试证明AECF为平行四边形.
★4.两组对角分别相等的四边形为平行四边形
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试证明四边形DFBE为平行四边形.
★5.对角线互相平分的四边形为平行四边形
如图,在□ABCD中,点E、F是对角线AC上两点,且AF=CE.求证:∠EBF=∠FDE.
培优升级检测
1、(成都)已知四边形ABCD,有以下四个条件: (AB∥CD (AB=CD (BC∥AD ④BC=AD 从这四个条件中任选两个,能使四边形ABCD为平行四边形的选法种数有( )
A.6种 B.5种 C.4种 D.3种
2、某广场有一个形状是平行四边形的花坛(如图)分别种有红黄蓝绿橙紫6得颜色的花,如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法错误的是( )
A.红花,绿花种植面积一定相等 B.紫花,橙花种植面积一定相等
C.红花,蓝花种植面积一定相等 D.蓝花,黄花种植面积一定相等
3、(陕西)如图,l1 ∥ l2 BE∥CF, BA⊥l1 DC ⊥l2,下面四个结论中(AB=DC; (BE=CF (S△ADE=S△DCF ④S□ABCD=S□BCFE,其中正确的有( )
A.4个 B .3个 C.2个 D .1个
4、、如图□ABCD中,BC=2AB,CE⊥AB,E为垂足,F为AD的中点,若∠AEF=54°,求∠B的度数.
5、如图,在直角坐标系中,A(0,1),B(0,3),P是x轴上一动点,在直线y=x上是否存在点Q,使以A、B、P、Q为顶点的四边形为平行四边形?若存在,画出所有满足情况的平行四边形,并求出对应的P、Q的坐标;若不存在,请说明理由.
6、在课外小组活动时,小慧拿来一道题和小东,小明交流.
题目:如图1,已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB,BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F,探究线段DF与EF的数量关系.
小慧同学的思路是:过点D作DG⊥AB于点G,构造全等三角形,通过推理使问题得解.
小东同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.
小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.
请你参考小慧同学的思路,探究并解决这三位同学提出的问题:
(1)写出题目中DF与EF的数量关系;
(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,题目中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;
(3)如图3,若∠ADB=∠BEC=2∠ABC,题目中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.
第十讲 平行四边形的性质和判定培优辅导答案
一、知识梳理
1.平行四边形:
(1)平行四边形的定义:两组对边 分别平行 的四边形是平行四边形.
平行四边形用符号 ∥ 表示.平行四边形ABCD记作 □ABCD ,读作平行四边形ABCD.
2.平行四边形的性质:平行四边形是 中心 对称图形,对称中心是 两条对角线的交点
(1)边: 平行四边形的对边平行且相等. 。 (2)角: 平行四边形的对角相等,邻角互补 。
(3)对角线: 平行四边形的对角线互相平分 。
(4)若一条直线过平行四边形两对角线的交点,则这直线被一组对边截下的线段以对角线的交点为中点,且这条直线 二等分 等分平行四边形的面积.
3.两条平行线间的距离:
(1)定义:两条平行线中, 一条直线上的任意一点到另一条直线的距离 ,叫做这两条平行线间的距离.
(2)两平行线间的距离 处处相等 .
4.平行四边形的面积:(1)如图①,.
(2)同底(等底)同高(等高)的平行四边形面积相等.
如图②,有公共边BC,则.
平行四边形的两条对角线把平行四边形分成四个面积相等的小三角形,如图有
5.平行四边形的判别方法:
平行四边形的判定的方法有从边的条件有:①两组对边_分别平行_________的四边形是平行四边形;
②两组对边__分别相等________的四边形是平行四边形;③一组对边_平行且相等___的四边形是平行四边形.
从对角线的条件有:④两条对角线__互相平分________的四边形是平行四边形.
从角的条件有:⑤两组对角___分别相等_______的四边形是平行四边形.
注意:一组对边平行另一组对边相等的四边形_____不是_____是平行四边形。
6.平行四边形知识的运用:
(1)直接运用平行四边形特征解决某些问题,如求角的度数,线段的长度,证明角相等或互补,证明线段相等或倍分等.
(2)识别一个四边形为平行四边形,从而得到两直线平行.
(3)先识别—个四边形是平行四边形,然后再用平行四边形的特征去解决某些问题.
二、重点突破
(一)平行四边形的性质
1、□ABCD的周长为60cm,其对角线交于O点,若△AOB的周长比△BOC的周长多10cm,则AB=_30__,BC=___10_____.
2、□ABCD中,对角线AC和BD交于O,若AC=8,BD=6,则边AB长的取值范围是_1
4、以不共线三点A、B、C为顶点的平行四边形共有___C____个.
5、如图,在□ABCD中,AE、AF分别垂直于BC、CD,垂足为E、F,若∠EAF=30°,AB=6,AD=10,则CD=_____6_____;AB与CD的距离为_____5_____;AD与BC的距离为___3_______;∠D=_____30°_____.
6、如图6,在平行四边形ABCD中,DB=DC、,CEBD于E,则 25° .
第6题图 第7题图 第8题图 第9题图
7、在平行四边形ABCD中,点A1、A2、A3、A4和C1、C2、C3、C4分别AB和CD的五等分点,点B1、B2和D1、D2分别是BC和DA的三等分点,已知四边形A4 B2 C4 D2的面积为1,则平行四边形ABCD面积为 .
8、已知平分,,,则 3 .
9、如图,平行四边形的周长为20cm ,AE⊥BC于E,AF⊥CD于F,AE=2 cm,AF=3 cm,求平行四边形ABCD的面积 12cm2 .
10、如图,△ABC是边长为1的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB交AC、BC于点E、F,作GH∥BC交AB、AC于点G、H,作MN∥AC交AB、BC于M、N,请你猜想EF+GH+MN的值是多少?其值是否随点P位置的改变而变化?并证明你的结论.
解:EF+GH+MN=8,其值不会随点P位置的改变而变化,理由如下:
∵MN∥AC,EF∥AB, ∴四边形AMPE是平行四边形, ∴PE=AM.同理PF=GB.∴EF=PE+PF=AM+GB ① ∵△ABC是等边三角形∴∠A=∠B=∠C=60° ∵GH∥BC∴∠AGH=∠B=60°,∠AHG=∠C=60° ∴△AGH是等边三角形 ∴GH=AG=AM+MG ② 同理MN=MB=MG+GB ③ ①+②+③得 EF+GH+MN=AM+GB+AM+MG+MG+GB=2(AM+MG+GB)=2AB=2x4=8 即EF+GH+MN=2AB=8.
(二)平行四边形的判定
★1.两组对边分别平行的四边形为平行四边形
已知:如图在□ABCD中,E、F分别在AD、BC上,且AE=CF,AF、BE交于G,CE、DF交于H.
求证:EF与GH互相平分.
解答 证明:∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC, ∴AE∥FC, ∵AE=FC, ∴四边形AFCE是平行四边形, ∴AF∥EC, ∵AD=BC,AE=FC, ∴ED=BF, ∵ED∥BF, ∴四边形EBFD是平行四边形, ∴∠EBF=∠EDF, ∵AF∥EC,AD∥BC, ∴∠AFB=∠ECB,∠ECB=∠CED, ∴∠AFB=∠CED, 在△BGF和△DHE中, ∴△BGF≌△HED(ASA), ∴GF=EH, ∴四边形EGFH是平行四边形.
∴EF与GH互相平分
★2.两组对边分别相等的四边形为平行四边形
如图,如图,△ABC中,AB=3,AC=4,BC=5,△ABD ,△ACE △BCF都是等边三角形,试证明四边形AEFD为平行四边形并求四边形AEFD的面积.
解:如图,△ABC中,AB=3,AC=4,BC=5, ∴BC2=AB2+AC2, ∴∠BAC=90°, ∵△ABD,△ACE都是等边三角形, ∴∠DAB=∠EAC=60°, ∴∠DAE=150°. ∵△ABD和△FBC都是等边三角形, ∴∠DBF+∠FBA=∠ABC+∠ABF=60°, ∴∠DBF=∠ABC. 在△ABC与△DBF中,
∴△ABC≌△DBF(SAS), ∴AC=DF=AE=4, 同理可证△ABC≌△EFC, ∴AB=EF=AD=3, ∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形). ∴∠FDA=180°-∠DAE=30°, ∴S?AEFD==3×(4×)=6. 答:四边形AEFD的面积是6.
★3.一组对边平行且相对的四边形为平行四边形
如图,□ABCD中,E、F分别在BA、DC的延长线上,且AE=AB,CF=CD,试证明AECF为平行四边形.
证明:∵四边形ABCD是平行四边形, ∴AB∥CD,AB=CD, ∵AE=AB,CF=CD
∵AE=CF
又∵AE∥CF
∴AECF为平行四边形.
★4.两组对角分别相等的四边形为平行四边形
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试证明四边形DFBE为平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,∠ADC=∠ABC
∵∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F
∴∠ADF=∠CDF=∠ADC,∠CBE=∠ABE=∠ABC,
∴∠ADF=∠CDF=∠CBE=∠ABE,
∵∠DFB=∠ADF+∠A ∠DEB=∠EBC+∠C
∴∠DFB=∠DEB且∠ABE=∠CDF
∴四边形DFBE为平行四边形.
★5.对角线互相平分的四边形为平行四边形
如图,在□ABCD中,点E、F是对角线AC上两点,且AF=CE.求证:∠EBF=∠FDE.
证明:连接BD交AC于O点, ∵四边形ABCD是平行四边形, ∴OA=OC,OB=OD, 又∵AE=CF, ∴OE=OF, ∴四边形BEDF是平行四边形, ∴∠EBF=∠EDF。
培优升级检测
1、(成都)已知四边形ABCD,有以下四个条件: (AB∥CD (AB=CD (BC∥AD ④BC=AD 从这四个条件中任选两个,能使四边形ABCD为平行四边形的选法种数有( C )
A.6种 B.5种 C.4种 D.3种
2、某广场有一个形状是平行四边形的花坛(如图)分别种有红黄蓝绿橙紫6得颜色的花,如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法错误的是( C )
A.红花,绿花种植面积一定相等 B.紫花,橙花种植面积一定相等
C.红花,蓝花种植面积一定相等 D.蓝花,黄花种植面积一定相等
3、(陕西)如图,l1 ∥ l2 BE∥CF, BA⊥l1 DC ⊥l2,下面四个结论中(AB=DC; (BE=CF (S△ADE=S△DCF ④S□ABCD=S□BCFE,其中正确的有( A )
A.4个 B .3个 C.2个 D .1个
4、、如图□ABCD中,BC=2AB,CE⊥AB,E为垂足,F为AD的中点,若∠AEF=54°,求∠B的度数.
解:延长EF与CD的延长线交于点G,连接CF,如图所示, ∵平行四边形ABCD, ∴CD∥AB,DC=AB,BC=AD, ∴∠AEF=∠G, ∵F为AD的中点,∴AF=DF, 又∠AFE=∠DFG, ∴△AEF≌△GDF(AAS), ∴FG=FE,∠G=∠AEF=54°, ∵CE⊥AB,CD∥AB, ∴EC⊥DC,即∠GCE=90°, 在Rt△CGE中,可得CF=GF=EF=GE,
∴∠FCG=∠G=54°, 又BC=AD=2AB=2DC,F为AD中点, ∴CD=FD, ∴∠DCF=∠CFD=54°, ∴∠B=∠CDA=180°-54°-54°=72°.
5、如图,在直角坐标系中,A(0,1),B(0,3),P是x轴上一动点,在直线y=x上是否存在点Q,使以A、B、P、Q为顶点的四边形为平行四边形?若存在,画出所有满足情况的平行四边形,并求出对应的P、Q的坐标;若不存在,请说明理由.
解:如1,∵P是x轴上一动点,点Q在直线y=x上,
∴设P(x,0),Q(a,a),
当AB是平行四边形的边时,
∵AB=3-1=2,∴PQ=AB=2,∴a=±2,
∴P1(-2,0),Q1(-2,-2)或P2(2,0),Q2(2,2);
如图2,当AB是平行四边形的对角线时,
BQ=AP是a2+(a-3)2=x2+12,即2a2-6a=x2-8①;
PB=AQ是a2+(a-1)2=32+x2,即2a2-2a=x2-9②.
①-②得a=4,把a=4代入①得,17=1+x2,
解得x=±4,
∴P3(-4,0),Q3(4,4)或P4(4,0),Q4(4,4)(舍去).
6、在课外小组活动时,小慧拿来一道题和小东,小明交流.
题目:如图1,已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB,BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F,探究线段DF与EF的数量关系.
小慧同学的思路是:过点D作DG⊥AB于点G,构造全等三角形,通过推理使问题得解.
小东同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.
小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.
请你参考小慧同学的思路,探究并解决这三位同学提出的问题:
(1)写出题目中DF与EF的数量关系;
(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,题目中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;
(3)如图3,若∠ADB=∠BEC=2∠ABC,题目中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.
解:(1)DF=EF;
(2)猜想:DF=FE; 证明:如图(1)所示,过点D作DG⊥AB于G,则∠DGB=90° ∵DA=DB,∠ADB=60°, ∴AG=BC,△DBA是等边三角形, ∴DB=BA, ∵∠ACB=90°,∠ABC=30° ∴AC=1/2AB=BG, ∴△DBG≌△BAC, ∴DG=BC, ∵BE=EC,∠BEC=60°, ∴△EBC是等边三角形, ∴BC=BE,∠CBE=60°, ∴DG=BE,∠ABE=∠ABC+∠CBE=90°, ∵∠DFC=∠EFB,∠DCF=∠EBF, ∴△DFC≌△EFB, ∴DF=EF;
(3)猜想:DF=FE; 如图(2)所示,过点D作DH⊥AB于H,连接HC,HE,HE交CB于K,则∠DHB=90°, ∵DA=DB, ∴AH=BH,∠1=∠HDB, ∵∠ACB=90°, ∴HC=HB, ∵EB=EC,HE=HE, ∴△HBE≌△HCE, ∴∠2=∠3,∠4=∠BEH, ∴HK⊥BC, ∴∠BKE=90°, ∵∠ADB=∠BEC=2∠ABC, ∴∠HDB=∠BEH=∠ABC, ∴∠DBC=∠DBH+∠ABC=∠DBH+∠HDB=90°, ∠EBH=∠EBK+∠ABC=∠EBK+∠BEK=90°, ∴DB∥HE,DH∥BE, ∴四边形DHEB是平行四边形, ∴BF=EF。
