江西省上饶市山江湖”协作体2018-2019高二下学期第一次月考数学(理)试卷
文档属性
| 名称 | 江西省上饶市山江湖”协作体2018-2019高二下学期第一次月考数学(理)试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 197.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-19 00:00:00 | ||
图片预览



文档简介
“山江湖”协作体2018-2019学年度第二学期高二年级第一次月考
数学试题(理)
满分:150分 考试时间:120分钟
一、选择题(本大题共12小题,每小题5分,共60分)
1.已知为虚数单位,若复数满足,则复数在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.函数y=sin2x的导数为( )
A.=2cos2x B. =(sin2x+2cos2x)
C. =2(sin2x+cos2x) D.=(2sin2x+cos2x)
3、等比数列中,前三项和为,则公比的值是( )
A. B. C.或 D.或
4.已知函数y=f(x),其导函数y=f′(x)的图像如图所示,则y=f(x) ( )
A.在(-∞,0)上为减少的 B.在x=0处取极小值
C.在x=2处取极大值 D.在(4,+∞)上为减少的
5.直线在第一象限内围成的封闭图形的面积为 ( )
A. B. C. 4 D.
6.设函数f(x)的导函数为f′(x),且f(x)=x2+2xf′(1),则f′(2)=( )
A.0 B.-4 C.-2 D.2
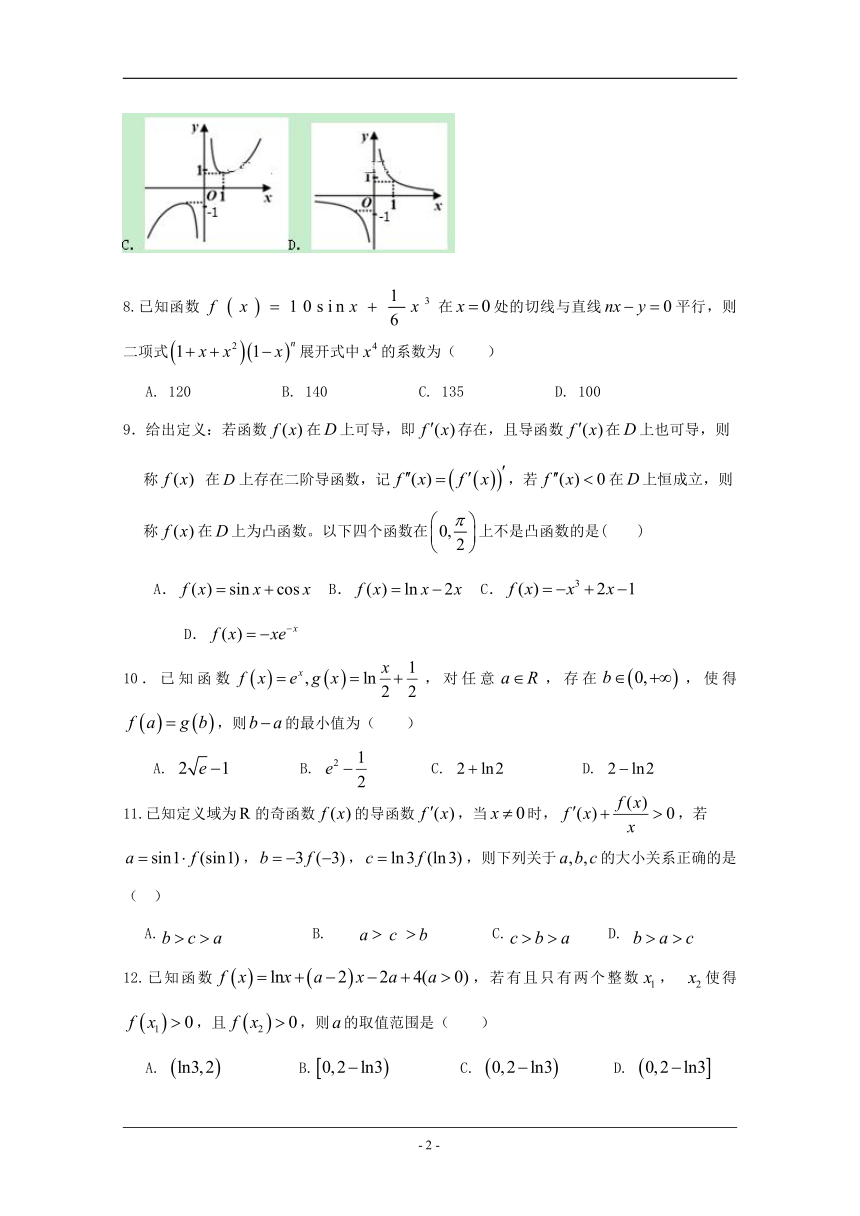
7.函数的部分图象大致为( )
8.已知函数在处的切线与直线平行,则二项式展开式中的系数为( )
A. 120 B. 140 C. 135 D. 100
9.给出定义:若函数在上可导,即存在,且导函数在上也可导,则称 在上存在二阶导函数,记,若在上恒成立,则称在上为凸函数。以下四个函数在上不是凸函数的是( )
A. B. C. D.
10.已知函数,对任意,存在,使得,则的最小值为( )
A. B. C. D.
11.已知定义域为的奇函数的导函数,当时,,若,,,则下列关于的大小关系正确的是( )
A. B. C. D.
12.已知函数,若有且只有两个整数, 使得,且,则的取值范围是( )
A. B. C. D.
填空题(每小5分,满分20分)
13.________________.
14.设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x+2,则函数y=f(x)的解析式为__________.
15.已知直线与曲线相切,则实数的值为________________.
16.已知函数的两个极值点分别为,且,若存在点在函数的图象上,则实数的取值范围是__________.
三、解答题(本大题共6小题,17题10分,其余每小题12分)
17.(本小题满分10分)
实数m取什么值时,复数是:①纯虚数;②实数;
18,计算下列定积分(本小题满分12分)
(1) (2) (3)
19.(本小题满分12分)
已知函数f(x)=x3+x﹣16.
(1)求曲线y=f(x)在点(2,-6)处的切线方程;
(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标.
20、(本题共12分)
如图,在半径为的半圆形(O为圆心)铁皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上,将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),记圆柱形罐子的体积为.
(1)按下列要求建立函数关系式:
①设,将表示为的函数;
②设(),将表示为的函数;
(2)请您选用(1)问中的一个函数关系,求圆柱形罐子的最大体积.
21. (本小题满分12分)
已知函数 (为实常数) .
(1)当时,求函数在上的最大值及相应的值;
(2)当时,讨论方程根的个数.
(3)若,且对任意的,都有,求实数a的取值范围.
22.(本小题满分12分)
已知函数.
(1)当时,求函数的极值;
(2)若函数有两个零点x1,x2,求的取值范围,并证明.
“山江湖”协作体2018-2019学年度第二学期高二年级第一次月考数学参考答案(理)
一、选择题(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
C
D
C
A
C
C
D
C
A
D
填空题(每小5分,满分20分)
13. 1 14 f(x)=x2+2x+1 15.1+ln2 16.(1,3)或(1三、解答题(本大题共6小题,共70分)
17.解(1)m=0或m=2 …………5分 (2)m=-3…………10分
18,解(1) e……4分 (2) +……8分 (3)…………12分
19.解:(1)∵f’(x)=(x3+x﹣16)'=3x2+1,
∴在点(2,﹣6)处的切线的斜率k=f′(2)=3×22+1=13,
∴切线的方程为y=13x﹣32.…………5分
(2)设切点为(x0,y0),则直线l的斜率为f'(x0)=3x02+1,
∴直线l的方程为y=(3x02+1)(x﹣x0)+x03+x0﹣16.
又∵直线l过点(0,0),∴0=(3x02+1)(﹣x0)+x03+x0﹣16,
整理,得x03=﹣8,∴x0=﹣2,∴y0=(﹣2)3+(﹣2)﹣16=﹣26,直线l的斜率k=3×(﹣2)2+1=13,∴直线l的方程为y=13x,切点坐标为(﹣2,﹣26)…………12分
20、解:(1)①,,
,()…………4分
②,,
,()………8分
(2)选用:,,
令,则
(2)选用:令,
,令,则,即
(对直接求导求解也得分,)
答:圆柱形罐子的最大体积为.…………12分
21.(1),当时,.当时,又,故,当时,取等号…………3分
(2)易知,故,方程根的个数等价于时,
方程根的个数。 设=,
当时,,函数递减,当时,,函数递增。又,,作出与直线的图像,由图像知:
当时,即时,方程有2个相异的根;
当 或时,方程有1个根;
当时,方程有0个根;……………8分
(3)当时,在时是增函数,又函数是减函数,不妨设,则等价于
即,故原题等价于函数在时是减函数, 恒成立,即在时恒成立。
在时是减函数 ……………11分
又a>0 所以a不存在……12分
22.【解答】解:(1)由,得,
当a≥0时,ax+1>0,若0<x<1,f'(x)>0;若x>1,f'(x)<0,
故当a≥0时,f(x)在x=1处取得的极大值;函数f(x)无极小值.…3分
(2)当a≥0时,由(1)知f(x)在x=1处取得极大值,且当x趋向于0时,f(x)趋向于负无穷大,又f(2)=ln2﹣2<0,f(x)有两个零点,则,解得a>2.当﹣1<a<0时,若0<x<1,f'(x)>0;若;,则f(x)在x=1处取得极大值,在处取得极小值,由于, 则f(x)仅有一个零点.
当a=﹣1时,,则f(x)仅有一个零点.
当a<﹣1时,若;若;
若x>1,f'(x)>0,则f(x)在x=1处取得极小值,
在处取得极大值,由于,则f(x)仅有一个 零点.
综上,f(x)有两个零点时,a的取值范围是(2,+∞).………7分
两零点分别在区间(0,1)和(1,+∞)内,不妨设0<x1<1,x2>1.
欲证x1+x2>2,需证明x2>2﹣x1,又由(1)知f(x)在(1,+∞)单调递减,故只需证明f(2﹣x1)>f(x2) =0即可.
,
又,
所以f(2﹣x1)=ln(2﹣x1)﹣ln(x1)+2x1﹣2,
令h(x)=ln(2﹣x)﹣lnx+2x﹣2(0<x<1),
则,
则h(x)在(0,1)上单调递减,
所以h(x)>h(1)=0,即f(2﹣x1)>0,
所以x1+x2>2.………(12分)
数学试题(理)
满分:150分 考试时间:120分钟
一、选择题(本大题共12小题,每小题5分,共60分)
1.已知为虚数单位,若复数满足,则复数在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.函数y=sin2x的导数为( )
A.=2cos2x B. =(sin2x+2cos2x)
C. =2(sin2x+cos2x) D.=(2sin2x+cos2x)
3、等比数列中,前三项和为,则公比的值是( )
A. B. C.或 D.或
4.已知函数y=f(x),其导函数y=f′(x)的图像如图所示,则y=f(x) ( )
A.在(-∞,0)上为减少的 B.在x=0处取极小值
C.在x=2处取极大值 D.在(4,+∞)上为减少的
5.直线在第一象限内围成的封闭图形的面积为 ( )
A. B. C. 4 D.
6.设函数f(x)的导函数为f′(x),且f(x)=x2+2xf′(1),则f′(2)=( )
A.0 B.-4 C.-2 D.2
7.函数的部分图象大致为( )
8.已知函数在处的切线与直线平行,则二项式展开式中的系数为( )
A. 120 B. 140 C. 135 D. 100
9.给出定义:若函数在上可导,即存在,且导函数在上也可导,则称 在上存在二阶导函数,记,若在上恒成立,则称在上为凸函数。以下四个函数在上不是凸函数的是( )
A. B. C. D.
10.已知函数,对任意,存在,使得,则的最小值为( )
A. B. C. D.
11.已知定义域为的奇函数的导函数,当时,,若,,,则下列关于的大小关系正确的是( )
A. B. C. D.
12.已知函数,若有且只有两个整数, 使得,且,则的取值范围是( )
A. B. C. D.
填空题(每小5分,满分20分)
13.________________.
14.设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x+2,则函数y=f(x)的解析式为__________.
15.已知直线与曲线相切,则实数的值为________________.
16.已知函数的两个极值点分别为,且,若存在点在函数的图象上,则实数的取值范围是__________.
三、解答题(本大题共6小题,17题10分,其余每小题12分)
17.(本小题满分10分)
实数m取什么值时,复数是:①纯虚数;②实数;
18,计算下列定积分(本小题满分12分)
(1) (2) (3)
19.(本小题满分12分)
已知函数f(x)=x3+x﹣16.
(1)求曲线y=f(x)在点(2,-6)处的切线方程;
(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标.
20、(本题共12分)
如图,在半径为的半圆形(O为圆心)铁皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上,将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),记圆柱形罐子的体积为.
(1)按下列要求建立函数关系式:
①设,将表示为的函数;
②设(),将表示为的函数;
(2)请您选用(1)问中的一个函数关系,求圆柱形罐子的最大体积.
21. (本小题满分12分)
已知函数 (为实常数) .
(1)当时,求函数在上的最大值及相应的值;
(2)当时,讨论方程根的个数.
(3)若,且对任意的,都有,求实数a的取值范围.
22.(本小题满分12分)
已知函数.
(1)当时,求函数的极值;
(2)若函数有两个零点x1,x2,求的取值范围,并证明.
“山江湖”协作体2018-2019学年度第二学期高二年级第一次月考数学参考答案(理)
一、选择题(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
C
D
C
A
C
C
D
C
A
D
填空题(每小5分,满分20分)
13. 1 14 f(x)=x2+2x+1 15.1+ln2 16.(1,3)或(1
17.解(1)m=0或m=2 …………5分 (2)m=-3…………10分
18,解(1) e……4分 (2) +……8分 (3)…………12分
19.解:(1)∵f’(x)=(x3+x﹣16)'=3x2+1,
∴在点(2,﹣6)处的切线的斜率k=f′(2)=3×22+1=13,
∴切线的方程为y=13x﹣32.…………5分
(2)设切点为(x0,y0),则直线l的斜率为f'(x0)=3x02+1,
∴直线l的方程为y=(3x02+1)(x﹣x0)+x03+x0﹣16.
又∵直线l过点(0,0),∴0=(3x02+1)(﹣x0)+x03+x0﹣16,
整理,得x03=﹣8,∴x0=﹣2,∴y0=(﹣2)3+(﹣2)﹣16=﹣26,直线l的斜率k=3×(﹣2)2+1=13,∴直线l的方程为y=13x,切点坐标为(﹣2,﹣26)…………12分
20、解:(1)①,,
,()…………4分
②,,
,()………8分
(2)选用:,,
令,则
(2)选用:令,
,令,则,即
(对直接求导求解也得分,)
答:圆柱形罐子的最大体积为.…………12分
21.(1),当时,.当时,又,故,当时,取等号…………3分
(2)易知,故,方程根的个数等价于时,
方程根的个数。 设=,
当时,,函数递减,当时,,函数递增。又,,作出与直线的图像,由图像知:
当时,即时,方程有2个相异的根;
当 或时,方程有1个根;
当时,方程有0个根;……………8分
(3)当时,在时是增函数,又函数是减函数,不妨设,则等价于
即,故原题等价于函数在时是减函数, 恒成立,即在时恒成立。
在时是减函数 ……………11分
又a>0 所以a不存在……12分
22.【解答】解:(1)由,得,
当a≥0时,ax+1>0,若0<x<1,f'(x)>0;若x>1,f'(x)<0,
故当a≥0时,f(x)在x=1处取得的极大值;函数f(x)无极小值.…3分
(2)当a≥0时,由(1)知f(x)在x=1处取得极大值,且当x趋向于0时,f(x)趋向于负无穷大,又f(2)=ln2﹣2<0,f(x)有两个零点,则,解得a>2.当﹣1<a<0时,若0<x<1,f'(x)>0;若;,则f(x)在x=1处取得极大值,在处取得极小值,由于, 则f(x)仅有一个零点.
当a=﹣1时,,则f(x)仅有一个零点.
当a<﹣1时,若;若;
若x>1,f'(x)>0,则f(x)在x=1处取得极小值,
在处取得极大值,由于,则f(x)仅有一个 零点.
综上,f(x)有两个零点时,a的取值范围是(2,+∞).………7分
两零点分别在区间(0,1)和(1,+∞)内,不妨设0<x1<1,x2>1.
欲证x1+x2>2,需证明x2>2﹣x1,又由(1)知f(x)在(1,+∞)单调递减,故只需证明f(2﹣x1)>f(x2) =0即可.
,
又,
所以f(2﹣x1)=ln(2﹣x1)﹣ln(x1)+2x1﹣2,
令h(x)=ln(2﹣x)﹣lnx+2x﹣2(0<x<1),
则,
则h(x)在(0,1)上单调递减,
所以h(x)>h(1)=0,即f(2﹣x1)>0,
所以x1+x2>2.………(12分)
同课章节目录
